晶片型压电换能器发电能力影响因素分析*

田晓超，林佳颖，王志聪，王 虎，张思达，杨志刚

(1.长春大学 机械与车辆工程学院，吉林 长春 130022；2.吉林大学 机械与航空航天工程学院，吉林 长春 130025)

0 引 言

近些年，压电材料作为新型智能和环保材料在各个领域发挥着重要作用，特别是,利用其正压电效应将机械能转化为电能的发电技术更是成为关注的焦点[1]。压电材料发电比传统电池更具有优势和前景，具有节能环保、寿命长、体积小、不受磁干扰等优点[2]。美国、日本、荷兰等许多国家大量开展了对压电发电与能量存储技术进行相关的研究[3～11]，国内对压电发电方面的技术研究也得到了快速的发展。

压电悬臂梁式发电具有结构简单、发电效率高等优点,备受广大研究学者的关注。在以往的研究中主要针对以下几个方面进行：通过对悬臂梁压电振子进行仿真分析和实验研究来探究其发电性能，拓宽悬臂梁压电发电装置的谐振频带, 提高其发电能力[12]；采用分段电极配置法提高压电振子在高频振动时的发电能力[13]；通过线性压电理论,分析压电晶片悬臂梁俘能器的输出功率与结构及外载荷阻抗等物理参数之间关系，得到优化负载阻抗、金属层厚度及金属层材料有效提高俘能器的俘能效率[14]；压电悬臂梁选择不同的位置配置质量块以提高装置开路电压和输出功率[15]；选择恰当的结构参数匹配使发电装置的固有频率接近外界的激振频率，提高发电性能[16]。

本文针对晶片型压电换能器结构参数对发电能力的影响因素进行研究，分析结构尺寸参数的最佳配比方案。

1 数学模型与仿真分析

1.1 数学模型

晶片型换能器尺寸参数模型如图1所示。换能器采用悬臂支撑方式，主要由金属基板、晶片陶瓷及质量块构成。压电换能器在力的作用下发生弯曲振动，由于压电材料的正压电效应，在压电晶片表面产生电荷，起到发电的效果。

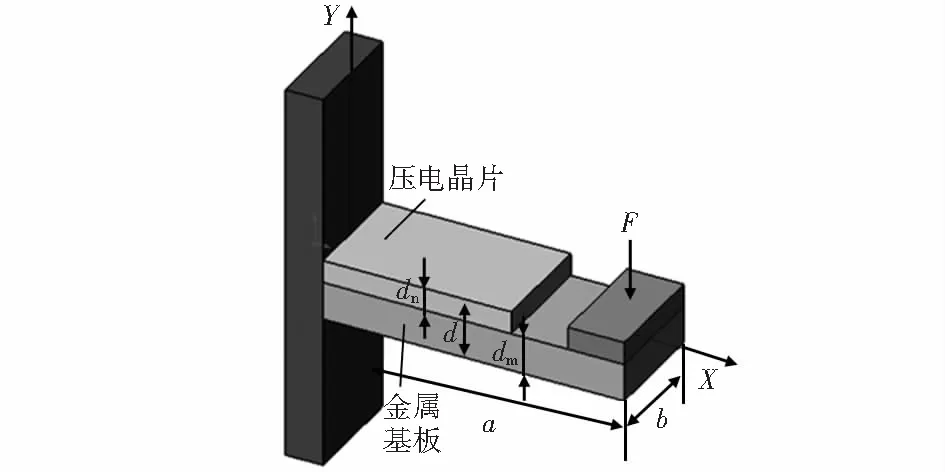
图1 压电换能器尺寸参数与模型

图1中，压电换能器总长为a,总宽为b,总厚为d，下标n与m分别为压电晶片和金属基板。设μ=dm/d为金属基板厚度dm与换能器的总厚度d的比值，得到压电晶片厚度为

dn=(1-μ)d

(1)

由材料的应变和应力方程得

(2)

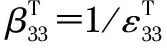
利用欧拉—伯努利方程得到晶片上表面到中心层的距离ys为

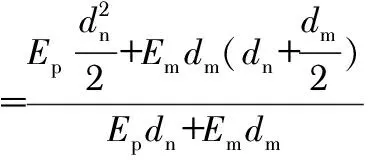
(3)

式中θ=Em/Ep为金属基板与压电陶瓷杨氏模量之比。

当压电换能器受到作用力时，其力矩方程表示为

M

=(x-a)F

(4)

式中Tm=EmS1为金属基板在x方向的应力。

由式(2)和式(4)得到曲率半径为

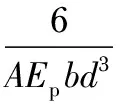
[2(1-μ+μθ)(x-a)F+μ(1-μ)θbd2g31EpD3]

(5)

式中A=μ4(1-θ)2-2μ(2μ2-3μ+2)(1-θ)+1。

将式(5)代入式(2)后,再对y积分，可得电压为

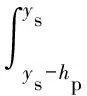
(6)

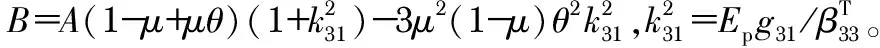
将式(6)表示成电位移为

(7)

对电位移面积积分得到换能器产生的电荷量

(8)

忽略自身产生的电压对整个发电装置的影响，单独由作用力产生的电荷为

(9)

由于电场公式Q=CfV和式(9)得到压电换能器的电容

(10)

由式(9)和式(10)得到压电换能器产生的电压为

(11)

1.2 仿真分析

质量块为5.2 g及激励振幅为1.8 mm时，对换能器厚度比、宽长比及杨氏模量之比进行仿真分析，得到结构参数与输出电压的相关曲线，测试结果如图2和图3所示。压电晶片材料参数如表1所示，金属基板材料参数如表2所示。

表1 压电晶片材料参数

表2 金属基板材料参数

从图2中可以看出，激励振幅为1.8 mm,厚度比为0.5,宽长比为1时，随着杨氏模量比的增加，输出电压先增大后减少，当杨氏模量比为1.1时，以黄铜为基板的换能器输出电压效果最佳。

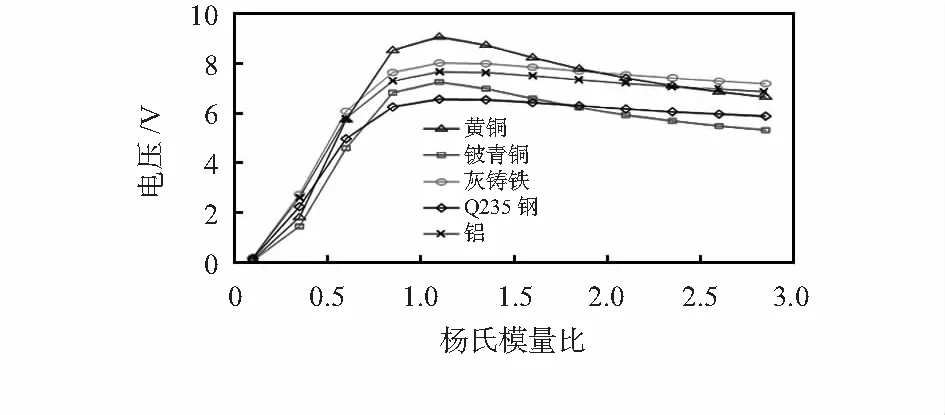
图2 杨氏模量比对发电能力的影响

从图3中可以看出，当以黄铜为基板，换能器厚度比为0.5时,发电能力最强，宽长比对换能器发电能力的影响先减小后增大，当宽长比接近于1时，压电换能器输出电压最佳。

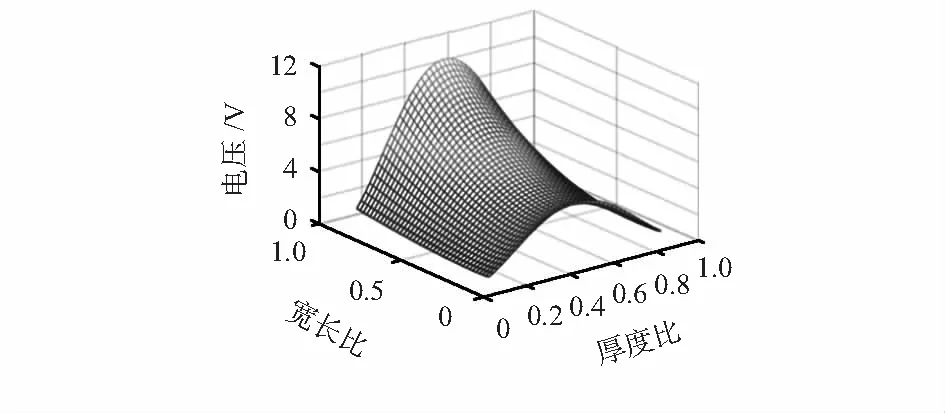
图3 厚度比、宽长比对发电能力的影响

2 实验测试与理论对比分析

2.1 测试装置

压电换能器发电测试装置如图4所示。测试系统主要由示波器、功率放大器、激振器、压电换能器样机、支撑架以及计算机组成。激振器用于激励换能器产生振动位移。在换能器的自由端配以5.2 g的质量块，改变压电晶片的尺寸与金属基板的材料属性，测试外界激励振幅、厚度比、杨氏模量比、宽长比对发电效果的影响规律。压电换能器尺寸参数如表3所示。

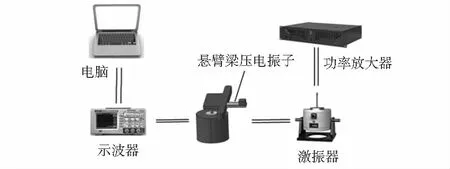
图4 实验测试装置

表3 压电换能器尺寸参数

2.2 输出电压与激励振幅关系

在宽长比为1，厚度比为0.5时，提供系统的激励频率为50 Hz，改变外部激励振幅，得到输出电压与激励振幅的关系，测试曲线如图5所示。

从图5中可以看出，压电换能器产生的电压与外部激励振幅成正比，仿真结果与实验测试曲线变化趋势相同。由此可知，振幅越大，换能器发生弯曲变形及应力也就越大，输出电压也随之变大。

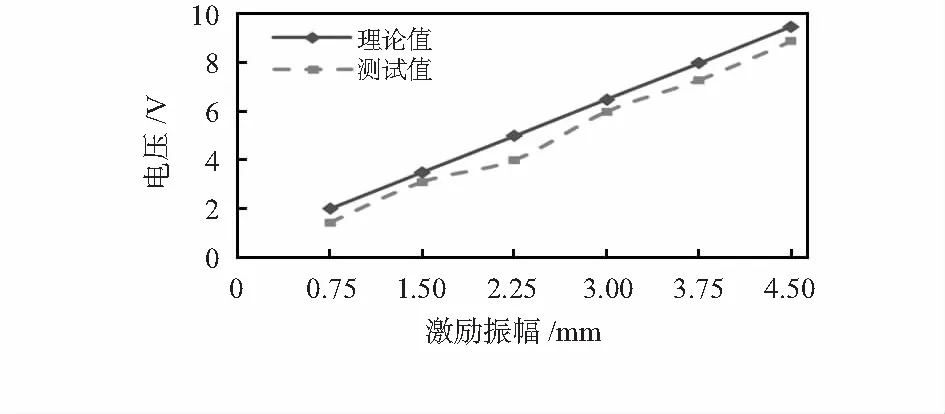
图5 输出电压与激励振幅的关系

2.3 输出电压与厚度比关系

在长宽比为1以及同样外部激励下压电换能器产生的电压与其厚度比关系曲线如图6所示。

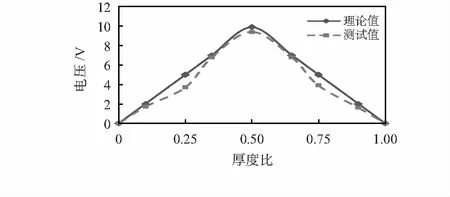
图6 输出电压与厚度比的关系

从图6中可以看出，仿真分析结果和测试结果相吻合，厚度比为0.5时,输出电压最大。

2.4 输出电压与宽长比的关系

在厚度比为0.5以及同样外部激励下压电换能器的电压输出与宽长比的关系曲线如图7所示。

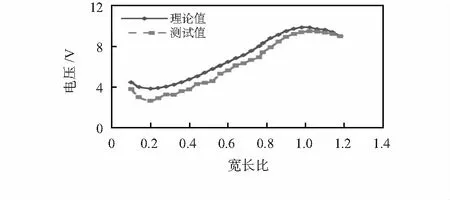
图7 输出电压与宽长比的关系

从图7中可以看出，压电换能器的电压输出随着宽长比先减小后增加，当宽长比为1时，换能器电能输出达到最佳。因此,在实际应用时，优先选用长和宽相等的压电换能器，以提高换能器的发电能力。

2.5 输出电压与杨氏模量比的关系

在同样外部激励下压电换能器的电压输出与杨氏模量比的关系曲线如图8所示。

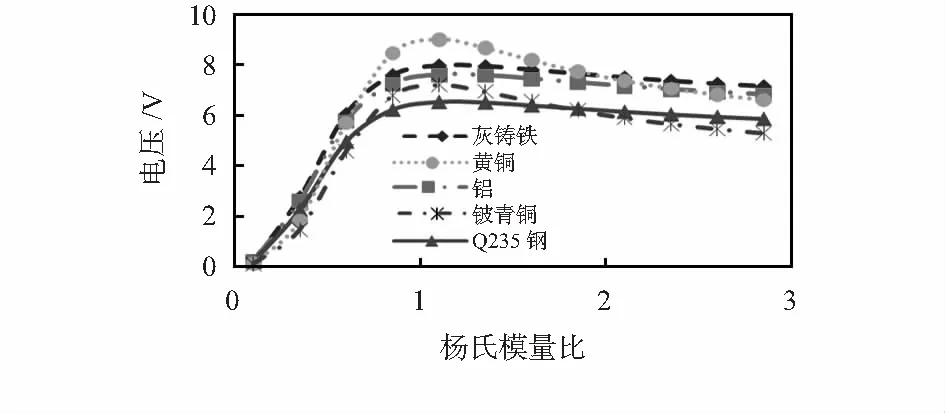
图8 不同金属基板输出电压与杨氏模量的关系

从图8中可以看出，当杨氏模量比小于1.1时，压电换能器的发电能力随杨氏模量比增大迅速增大，在比值为1.1时，黄铜基板的发电效果最佳，当杨氏模量比大于1.1时，压电换能器的发电能力逐渐减弱。

3 结 论

建立了晶片型压电换能器发电模型，利用MATLAB对发电模型进行了仿真分析。通过实验测试分析结构参数对换能器发电影响关系，理论分析与实验测试结果相吻合。压电换能器输出的电压与激励振幅成正比，输出电压随厚度比、宽长比以及杨氏模量比先增加后减小。当厚度比为0.5,宽长比为1,杨氏模量为1.1时，压电换能器输出电压效果最佳。