例析构造法在直线和圆中的应用

侯有岐

(陕西省汉中市四○五学校 723312)

“数形结合”是重要的数学思想方法之一,著名数学家华罗庚说:“数缺形时少直观，形少数时难入微”,这就要求我们在使用图象解题时,必须充分理解题意,画出比较准确的图象,注意图象中元素间关系,不能主观臆断,导致图形失真,从而得出错误答案,甚至无法求解.为此,本文例析怎样根据题意按要求准确作图,利用构造法在直线和圆的应用中快速解题.

1 构造“斜率”求最值(范围)

图1

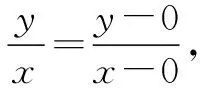
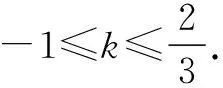
2 构造“距离”求最值(范围)

(2)已知实数x,y满足5x+12y+60=0，求x2+y2的最小值.

(3)已知实数x,y满足方程x2+y2-4x+1=0，求y-x的最小值.

即问题转化为在x轴上求一点P(x,0)与A(1,1),B(2,2)的距离之和的最小值.

图2

(2)x2+y2的最小值为坐标原点到直线5x+12y+60=0距离的平方.

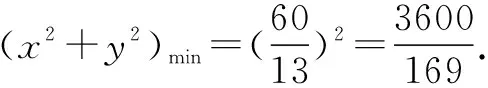
(3)设y-x=b，则y=x+b，当且仅当直线y=x+b与圆切于第四象限时，纵截距b取最小值.

点评涉及与圆有关的最值问题，可借助图形性质，利用数形结合求解，一般地：

(2)形如t=ax+by的最值问题，可转化为动直线截距的最值问题．

(3)形如(x-a)2+(y-b)2的最值问题，可转化为定点到动直线的最值问题，或圆心已定的动圆半径的最值问题．

例3 某地两邻镇在一直角坐标系下的坐标为A(1,2),B(4,0), 一条河所在的直线方程为l:x+2y-10=0, 若在河边l上建一座供水站P,使它到A,B两镇的管道最省,问应建在什么地方?

分析利用平面几何(两点之间线段最短;三角形两边之和大于第三边)及解析法确定点P的位置.

解析如图3,过点A作直线l的对称点A′,连接A′B交l于点P,则点P即为所求.这是因为:

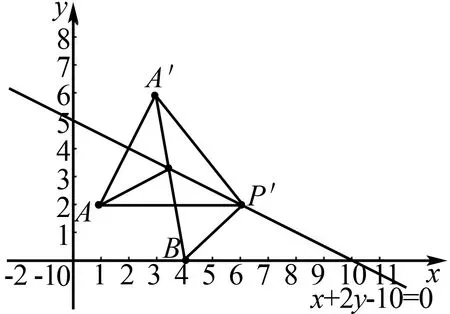
图3

若在点P′(异于点P),|AP′|+|P′B|=|A′P′|+|P′B|>|A′B|.

因此,只能在点P处取得最小值.

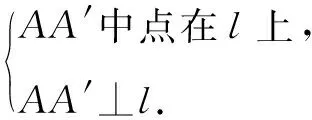
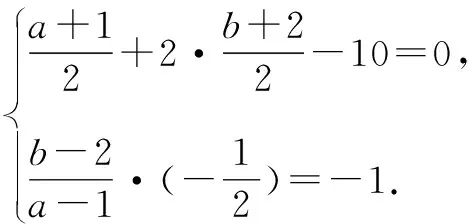
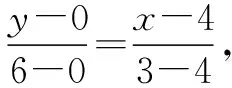
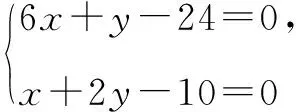
点评(1)凡是路程之和最近问题都要用关于直线对称的点进行处理.通过图形直观、对比分析，可以较好地突破理解上的难点,达到化难为易,化繁为简的目的.事实上：

当点A,B在直线l异侧时，点P即为直线AB与直线l交点；当点A,B在直线l同侧时，可通过某一点关于直线l对称转为异侧解决.

(2)若在直线l上求一点Q，使||QA|-|QB||最大，可根据三角形两边之差小于第三边，仿此解决，但此时：

当点A,B在直线l同侧时，点Q为直线AB与直线l交点；当点A,B在直线l异侧时，可通过某一点关于直线l对称转为同侧解决.

3 构造“圆”求直线条数

例4 在坐标平面内,与点A(1,2)距离为1,且与点B(3,1)距离为2的直线共有( )条.

A.1 B.2 C.3 D.4

分析本题若直接求解,将无从下手,若将数的问题辅以形的意义, 就能利用圆的定义画出分别以A(1,2),B(3,1)为圆心，以1,2为半径的两个圆,然后再根据两圆的位置关系,把问题转化为研究两圆的公切线的条数.

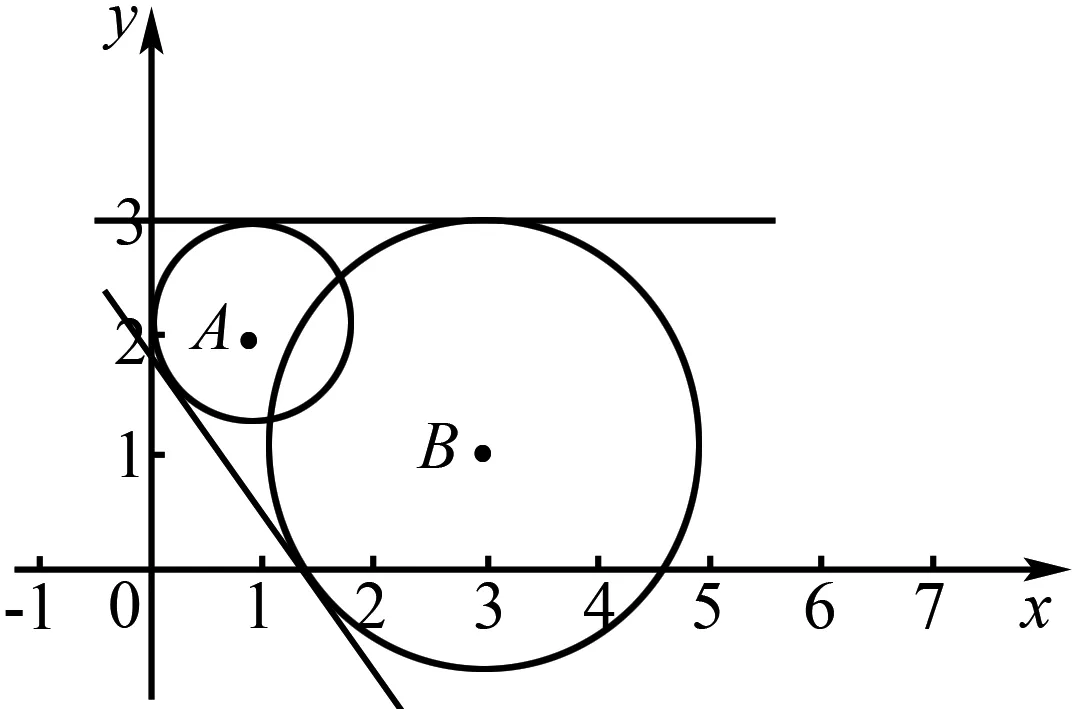
图4

解析作圆A(rA=1), 圆B(rB=2),

则符合题意的直线是圆A, 圆B的公切线.

因为两圆圆心距

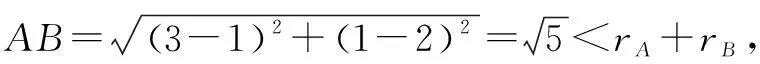
所以圆A与圆B相交,所以公切线有两条.

所以符合题意的直线共有两条,故选B.

点评概念是反映客观事物本质属性的思维形式,一般比较抽象,在理解上有一定困难,若通过正确作图,借助几何直观真正把握概念的实质内涵,从而为解题开启新的思路,提供新的途径,达到化隐为显的目的.

由以上四例可知,只有根据几何意义正确构造图形,借助几何直观,运用数形结合思想,才可以避免繁琐推理和复杂运算,并展现问题本质,实现解题突破和解题优化,因而应引起同学们的高度重视.

4 变式训练

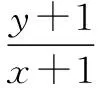
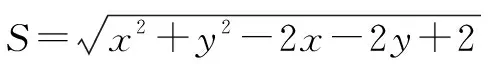
题3 已知a,b,c为某一直角三角形的三边长，c为斜边长，若点P(m,n)在直线ax+by+2c=0上，则m2+n2的最小值为____.