例谈累加法求数列通项公式的求解策略
2022-12-10江中伟
江中伟
(广东省梅州市虎山中学 514299)
利用累加法求数列的通项公式是很常用的一种方法,但在教学中学生实际上掌握得并不是很理想.根据本人的教学实践,本文把累加法求数列通项公式的方法细化,分门别类,总结类型和方法.对于an-an-1=f(n)(n≥2),利用累加法求数列的通项公式an=a1+f(1)+f(2)+f(3)+…+f(n-1),把它总结为六种类型及对应的求解方法.
1 常规型
例1 在数列{an}中,已知a1=2,an+1-an=2n(n∈N*),则a50=____.
分析由an+1-an=2n,得
a2-a1=2×1,
a3-a2=2×2,
a4-a3=2×3,
……
an-an-1=2(n-1)(n≥2),
以上n-1个式子相加可得
又a1=2,所以an=n2-n+2(n≥2).
故a50=2500-50+2=2452.
例2 在数列{an}中,已知a1=2,an+1-an=2n(n∈N*),则a9=____.
分析由a1=2,an+1-an=2n可得
a2-a1=2,
a3-a2=22,
a4-a3=23,
……
an-an-1=2n-1(n≥2),
以上n-1个式子相加可得
an-a1=2+22+23+…+2n-1=2n-2.
所以an=2n-2+a1=2n.
故a9=29=512.
点评是否能利用累加法,首先要看能否将数列的递推公式整理成an-an-1=f(n)(n≥2),或者an+1-an=f(n)的形式,其次还要用到等差数列或等比数列的前n项和公式.
2 换元型
例3 在数列{an}中,已知a1=13,(n+1)an+1-nan=2n+1(n∈N*),则下列说法正确的是( ).
A.an+1≥an
B.an+1≤an
C.数列{an}的最小项为a3和a4
D.数列{an}的最大项为a3和a4

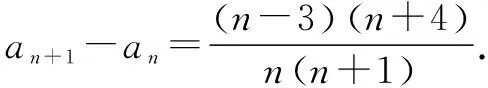
从而可得a1>a2>a3=a4 点评本题考查构造新数列,运用累加法求数列的通项公式,以及运用作差法判断差的正负得出数列的增减性,这是利用换元等差累加法求数列通项公式. 利用累加法得 =b1+lnn. 当n=1时a1=2也适合上式, 故an=2n+nlnn(n∈N*). 点评本题考查构造新数列,运用累加法求数列的通项公式,以及运用对数的运算性质,这是利用换元对数累加法求数列通项公式. 利用累加法可得 所以数列{bn}是单调递增数列. 因此当n=1时,bn即nan的最小值为1. 点评对已知式子如何变形是解题的关键,本题抓住等式两边同除以anan+1后,再裂项利用累加法求解,这是同除裂项累加型求数列通项公式. 分析两边同时除以n(n+1)anan+1可得 点评本题主要考查数列的递推公式的应用,合理利用“裂项法”和“累加法”求解是解答的关键,着重考查了推理与运算能力,这是双同除系数裂项累加型求数列通项公式. 例9 在数列{an}中,已知a1=1,an+1=an+(-1)nn(n∈N*),则a20=____. 分析由已知可得,当n为奇数时,则an+1-an=-n;当n为偶数时,则an+1-an=n. 利用累加法可得a20-a1=-1×9+(-1). 即a20=-9. 例10 在数列{an}中,已知a1=1,a2n-1+2a2n=1-22n-1,2a2n+a2n+1=1+22n(n∈N*),求a2n-1. 故a2n-1=22n-1-1. 点评此题的难点是从已知条件中找到关系式:a2n+1-a2n-1=22n+22n-1=3×22n-1,然后利用累加法即可求解. 在例习题教学中要使学生真正理解和掌握解题方法,教师必须选择有代表性的例习题,分门别类,举三反一,帮助学生归纳总结解题方法,学生才能做到举一反三,把方法弄懂弄透,提高解题能力,提升数学核心素养.


3 裂项型

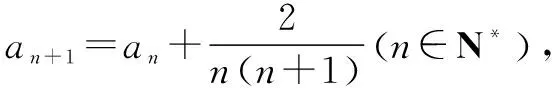
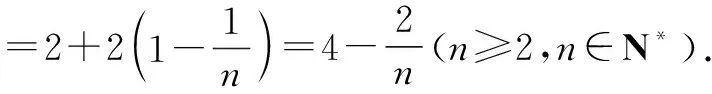
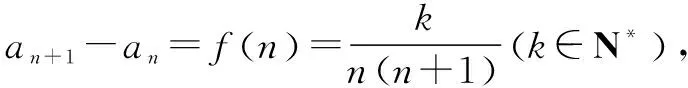




4 同除裂项型


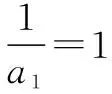


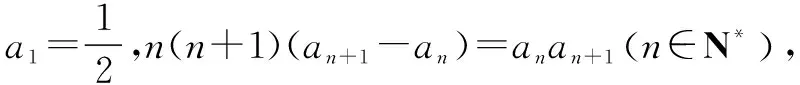


5 奇偶正负讨论累加型
6 累加型综合难题