依托几何直观合理运算求解——对2022年新高考Ⅰ卷第21题(1)的多解及推广

叶诚理 林品玲 俞 燕

(福建省福清第一中学 350300)

1 试题呈现

2 试题分析

本题考查双曲线的标准方程、直线与双曲线的位置关系、双曲线内接三角形的面积；考查抽象概括能力；考查化归与转化思想、数形结合思想；考查数学抽象、直观想象、数学运算等核心素养；体现基础性、综合性、创新性.

本题宽入口，解法多样，关键是如何将几何条件进行代数化表征，是值得欣赏和拓展的一道好题.

3 “本手”探析

易知直线l的斜率存在.

设l:y=kx+m，P(x1,y1),Q(x2,y2)，

(1-2k2)x2-4mkx-2m2-2=0.

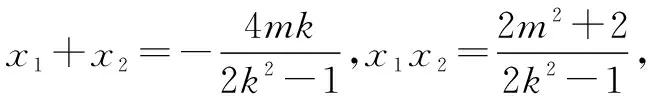
Δ=16m2k2+4(2m2+2)(2k2-1)>0.

所以m2-1+2k2>0．

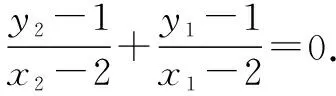
即2kx1x2+(m-1-2k)(x1+x2)-4(m-1)=0.

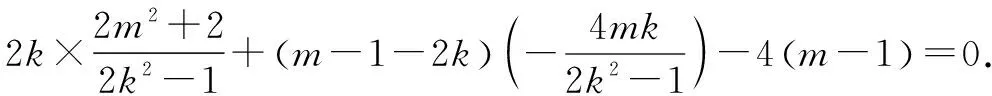
化简,得(k+1)(2k-1+m)=0.

所以k=-1或m=1-2k.

又当m=1-2k时，直线l:y=k(x-2)+1过点A(2,1)，与题意不符，舍去，故k=-1．

我们不难发现常规解法思路简洁，但计算量较大，关键是能否对条件“直线AP,AQ的斜率之和为0”这个几何条件进行有效转化．故本文接下去对第(1)问的求解进行多角度的探析．

4 “妙手”赏析

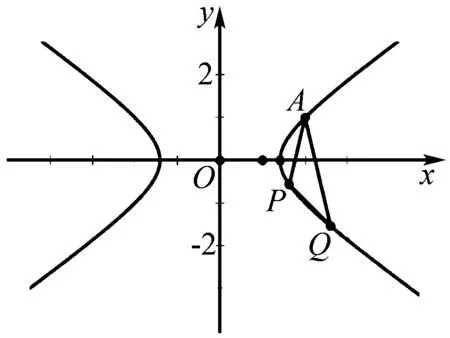
图1

(x-2)[(2k2-1)x-2(2k2-2k+1)]=0.

用-k替换k，得

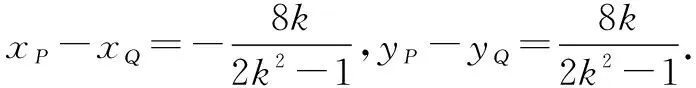
方法2(切线法)当∠PAQ→0时，依题意，点P→点Q，设点A(2,1)关于x轴的对称点为A′(2,-1)，此时，割线PQ的极限位置是过点A′的切线，于是直线l的斜率就等于过点A′的切线的斜率.

由kAP=-kAQ，则kOM=-kON.

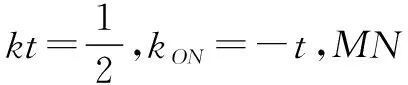
所以MN∥PQ.

即kl=kMN=-1．

方法4 (同构法)设直线PQ斜率为k，直线AP斜率为k1，直线AQ斜率为k2，则k,k1,k2互不相等，且k1+k2=0.

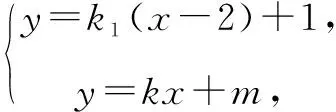
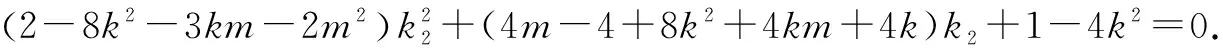
故k1,k2为关于K的一元二次方程(2-8k2-3km-2m2)K2+(4m-4+8k2+4km+4k)K+1-4k2=0的两个实根.

由k1+k2=0，得4m-4+8k2+4km+4k=0.

即(k+1)(m+2k-1)=0.

当m+2k-1=0时，直线PQ过点A(2,1)，不符题意舍去，故kl=-1．

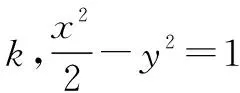
得(x-2)2+4(x-2)-2(y-1)2-4(y-1)=0.

两边同除(x-2)2,得

由m(x-2)+n(y-1)=1，代入上式,得

(2+4n)k2+(4m-4n)k-1-4m=0.

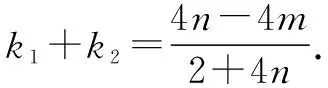
设kAP=k,kAQ=-k，P(x1,y1),Q(x2,y2)，则

lAP:y=kx,lAQ:y=-kx，

即(1-2k2)x2+(4-4k)x=0.

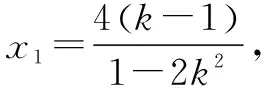
5 推广拓展

事实上，本题有其深厚的几何背景，由切线法得到本题的一般性推广：

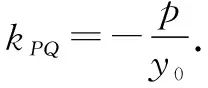
6 教学启示

在高三解析几何的教学中，我们要注重引导学生理解解析几何的基本思想，要求学生必须有画图、析图、用图的意识和习惯；立足概念、返璞归真，重视挖掘图形的几何特征，巧妙转化，培养直观想象素养；合理引入参数，进行多元表征，将几何条件代数化，培养逻辑推理素养，掌握坐标法、待定系数法、模型构造法、设而不求整体运算等技巧力争减少运算量，培养运算素养；在图形运动变化中探究运动变化规律，把握数学本质，运用特殊与一般思想，动中取静，以静制动，感受数学的美和哲学的思辨．