反事实量子调控研究进展

李振娅,李征鸿

(上海大学理学院,上海 200444)

21世纪的前20年,是量子科技爆发式发展的20年.随着“墨子号”量子卫星的升空以及量子霸权争夺战的兴起,量子力学不仅从专业书籍走进了普通大众的视野,也逐渐展示出其在国家安全、社会经济高质量发展中的重要作用.目前,量子通讯[1-2]、量子计算[3-4]等量子信息学的研究受到了广泛的重视和支持,并在众多科学家的共同努力下朝着实用化和商业化的方向迅速发展.另外,新的技术和研究也催生了新的认知和应用前景.本工作的基础——反事实量子直接通讯方案(direct counterfactual quantum communication)[5],便是在这样的大环境下诞生的.它展示了一种极其反直觉的量子现象,即信息可以在没有任何实际物质交换的情况下被远程传输.通过近10年的研究,人们对这种非局域量子现象的物理本质有了更深入的认知,同时也注意到反事实量子直接通讯的背后蕴含着一种非局域的量子调控方式,该调控通过多重量子测量来实现.针对这一新型的量子调控方式,人们对其可能的应用做了大量研究,内容涉及量子通讯、量子计算和量子探测等.我们预期,该方向的成果将对样本无伤量子成像、隐身量子雷达等新技术的发展起到关键作用.本工作将从反事实量子调控的概念、基础理论、实验验证和相关应用等多个方面进行阐述和介绍.

1 反事实量子调控

假设有两个相距遥远的客体,初始时刻二者没有相互纠缠,是完全孤立的.反事实量子调控是指其中一方在没有任何实际物质传输和能量交换的条件下,影响另一方的状态演化,使之产生可分辨的变化.通俗的讲,便是心灵感应或者心灵控制——不依赖任何媒介的隔空控制方式.虽然在量子力学中,利用量子纠缠也能产生类似的结果,但是反事实量子调控的特质在于,它既可以远程隔空形成纠缠,也可以在没有纠缠的情况下直接实现远程调控.这是一种完全的非局域量子调控手段,显然,这是一种非局域的调控手段,其研究始于反事实量子直接通讯,即对一个单光子的传播路径的非局域调控,而其理论根基则是无相互作用测量(interaction-free measurement)和量子芝诺效应(quantum Zeno effect).考虑到反事实量子调控与人们在经典世界的认知完全相悖,下面将对相关的概念逐一介绍以便读者有更形象的理解.

1.1 EV炸弹检测实验和无相互作用测量

无相互作用测量的理论探讨最早可以追溯至20世纪80年代Dicke[6]的工作.1993年,Elitzur等[7]提出了一个简洁明了的思想实验——EV炸弹检测实验,极大地推进了无相互作用测量研究的相关工作.实验假设有一种装备了单光子引信的炸弹,炸弹的引信只需吸收一个单光子便可触发.若引信失效,则其对光子透明.实验的要求是在不触发炸弹的情况下,尽可能鉴定出未失效的炸弹,具体的探测方案如图1所示.被检测的炸弹被放置在干涉仪的右路径上,当一个单光子入射进入干涉仪后,由于光分束器(beam splitter,BS)的作用和单光子不可再分性,光子将形成以下两个状态的叠加态:①光子处于左干涉臂;②光子处于右干涉臂.如果引信是透明的,则由于左右路径的干涉作用,光子将只可能在D1端输出.然而,若炸弹引信是完好的,则由于光子出现在右光路的概率为50%,炸弹被引爆的概率为50%.但如果炸弹没有被触发,则说明光子的实际路径必然是在干涉仪的左侧.结果是D0和D1各有25%的几率找到光子.这里的重点在于:如果最终是D0找到了光子,则可以确认炸弹的引信是完好的.注意到此时光子并没有经过炸弹所在位置,二者之间没有实际“接触”,炸弹不会爆炸,这便是无相互作用测量.

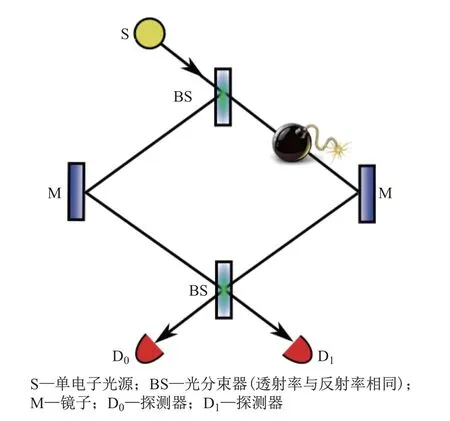
图1 EV炸弹测试问题Fig.1 EV bomb testing

1.2 量子芝诺效应下的无相互作用测量

EV炸弹检测实验中采用非接触的方式安全地找出炸弹的概率仅为25%.1995年,Kwiat等[8]利用量子芝诺效应,成功将此概率提升至100%.量子芝诺效应是指持续的量子观测能抑制系统的演化[9-11].图2为量子芝诺效应下无相互作用测量的链式干涉仪结构,其中炸弹位于链中每个干涉仪的上干涉臂,简单起见,假设所有的炸弹都是相同状态的(透明或者不透明).与EV炸弹检测实验不同的一点是,这里使用的BS的反射率远大于透射率.测量开始后,要求单光子连续通过BS以反复“感受”炸弹的影响.如果炸弹是透明的,则上下两侧光路之间的干涉过程会持续通过BS发生,从而使得光子在上下光路的概率分布“重心”逐渐从下光路转移至上光路,最终D1探测器找到光子的概率为100%.与之相对,如果炸弹都是非透明的,则炸弹对光子的持续吸收作用会抑制光子的路径演化过程.这将导致光子会滞留在下光路,并最终造成D0的触发,其概率在理想条件下亦为100%.换言之,结合量子芝诺效应和无相互作用测量,能够在完全不触发炸弹的情况下判别炸弹的好坏.

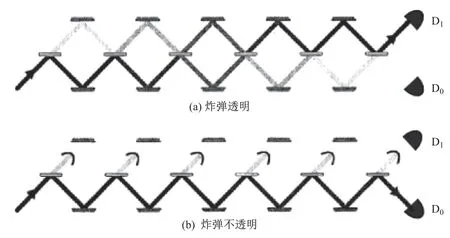
图2 量子芝诺效应下的无相互作用测量[8]Fig.2 Interaction-free measurement with quantum Zeno effect[8]

1.3 反事实量子直接通讯

Kwiat等[8]提出的无相互作用测量展示了一种在经典世界中匪夷所思的测量方式,其结果已经让人们非常震惊,但这只是故事的开始.人们注意到,当炸弹为透明时,光子还是会穿过炸弹从而和炸弹发生“接触”.事实上,穿过物体会伴随有相位累计,因而这并不能算是真正的无相互作用.于是一个更“猎奇”的想法便诞生了:是否存在一种可能,即无论炸弹的状态为何,光子都不会和炸弹接触(光子的传播路径不包含炸弹所在位置),但却能真实反应炸弹的状态信息呢？研究发现,利用嵌套干涉仪链结构[5,12],这个“天方夜谭”在量子力学框架下却是完全可能的.特别地,如果炸弹的状态代表信号0和1,则信息便可以非局域地、在没有预制纠缠和任何物质信息载体输运的条件下“隔空”传递给光子,这便是反事实量子直接通讯协议[5].为了读者更好的理解,接下来先简单描述反事实量子直接通讯中的物理过程,再详细地介绍理论计算证明.

图3(a)为反事实量子直接通讯协议的光学结构,该结构由嵌套的干涉仪链构成.左侧的大干涉仪链(由M个BSM构成)称为外链;每一个干涉仪的右侧都嵌套一个小干涉仪链(由N个BSN构成),称为内链.单个干涉仪链的功能和Kwiat等[8]提出的一致.在内链的每一个干涉仪的右臂上,均有一个可开关的探测器SD,其关闭时是透明的,而打开时则会吸收光子并完成测量.假定所有SD的行为保持一致,现在描述SD对于光子传播路径的影响.考虑一个单光子从外链的左侧入射,如果SD是非透明的,则任何进入内链的光子由于量子芝诺效应的作用将会被封闭在内链的左侧,从而对于外链来说,干涉过程将持续发生,最终光子将完全地导入到D1端,在理想条件下其概率为100%.注意到单光子不可分割,D1接收到光子则意味着所有的SD都是静默的,光子不会和它们发生“接触”.与上述情况相对,如果SD是透明的,则量子干涉在内链内部发生,这使得任何进入内链的光子都将被引导至D2,而不会通过内链的左侧出口返回外链.换言之,此时整个内链可视作为一个探测器.这也意味着,对于外链来说,量子芝诺效应将会抑制量子干涉过程,光子会被封闭在外链的左侧,根本不会进入内链中.最终,D0接收到光子的概率为100%.更重要的是,D0接收到光子意味着探测器D2没有接收到光子.换言之,整个内链都没有光子进入,SD必然也不会和光子有任何“接触”.综合上述两种过程可以看到,SD的状态非局域地操控了光子的路径演化过程,并决定了光子的终态.显而易见,如果SD的状态代表信息0/1,而光子代表信息接收器,则信息可以非局域地从SD处向光子传输.

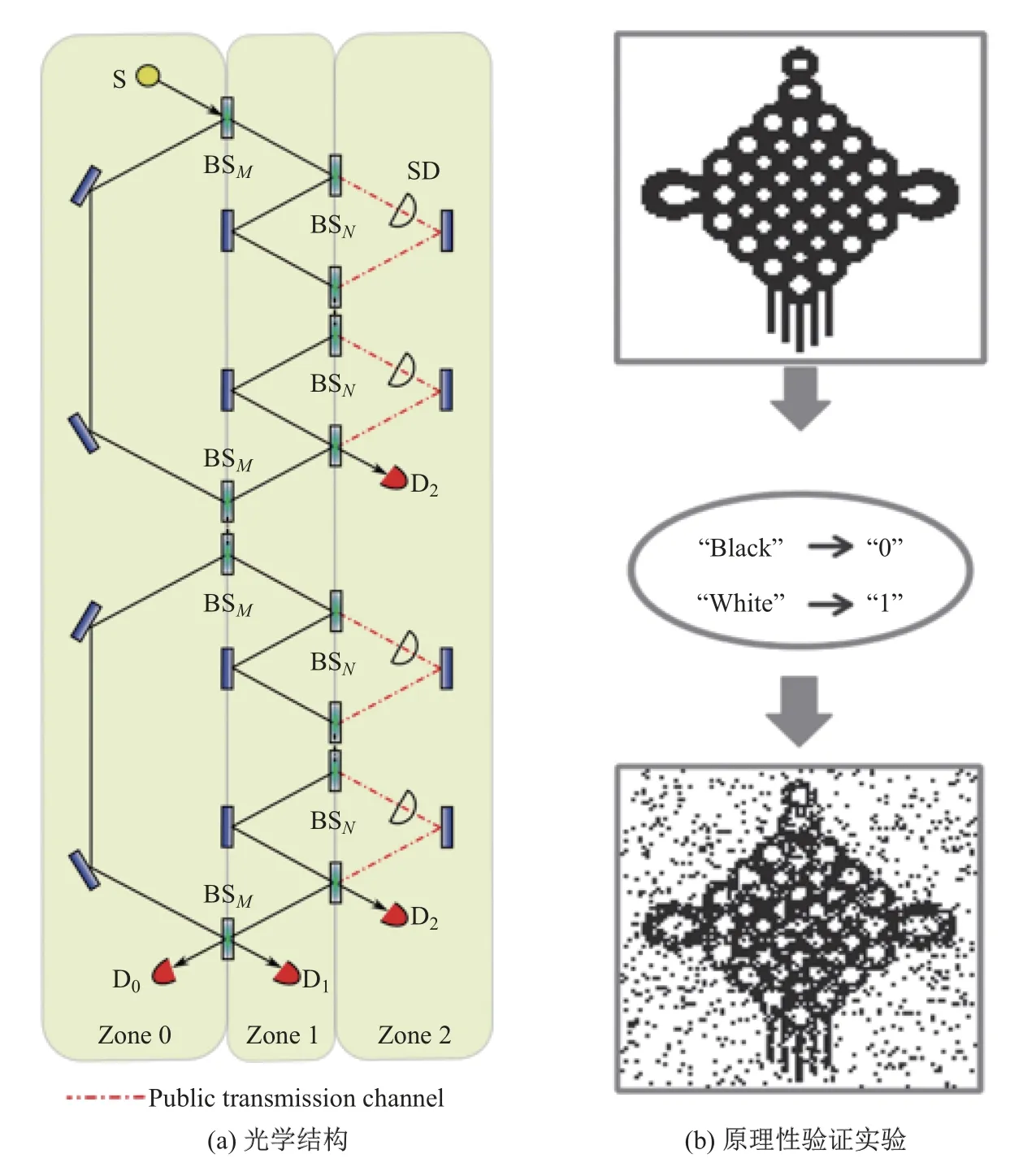
图3 反事实量子直接通讯协议的光学结构示意图和原理性验证实验结果[20]Fig.3 Scheme of direct counterfactual quantum communication protocol and experimental results[20]

2 反事实量子调控的基础理论

反事实量子直接通讯协议的非局域的特性引发了大量的理论研究,同时其独特的调控方式亦引发了众多的应用性研究.在具体展开之前,首先给出反事实量子调控的基础理论和证明.需要说明的是,到目前为止,反事实量子调控研究是基于单光子源的.而Li等[13]的研究显示,单光子光源并非反事实量子调控的必要条件,仅仅是Fock态光源的一个特例.注意到任意光子数分布总可以用Fock态的展开来描述,因此借由Fock态光源下的研究成果,可以探讨任意多光子光源下的反事实量子调控,实现对多光子的集体非局域调控,即使大量光子像一个单光子一般集体行动.这无论在物理机制上,还是在应用层面上都是极其重要的.对于多光子光源的运用将是反事实量子调控研究的下一个重要阶段.因此,这里直接采用Fock态光源来进行论述.

为了方便计算,将图3(a)分为3个区域:区域0覆盖BSM的左侧,区域1包含位于BSM和BSN之间的光路径,区域2为BSN右侧路径.接下来证明被调控的光子将被限制在区域0和1,但能如实反映远端SD的状态.另外,区域2中的红色点画线代表控制端和被控制端之间的公开区域(公开传输信道),该区域在整个调控过程中都不会有任何光子出现.

按照区域划分,假设b0、b1和b2分别代表3个区域内的光场湮灭算符,则BSM(N)的功能表达式为

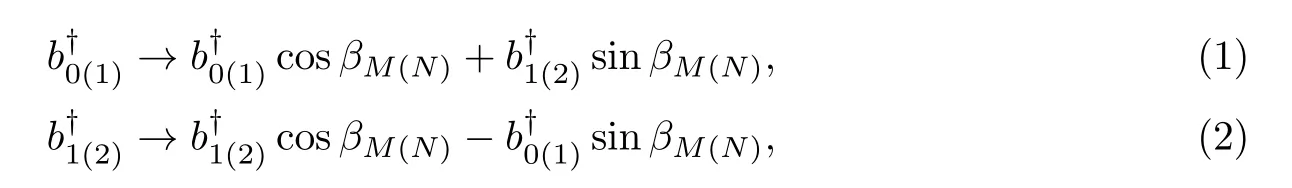
式中:βM(N)=π/2M(N),M(N)为外(内)链中的BSM(N)的个数;cos2βM(N)为BSM(N)的反射率.

利用式(1)和(2)给出的迭代关系,该初态经过第一个BSM和第一个BSN后变为

之后,按照SD的不同状态,光子的演化也会产生差别.

情况1 SD为透明.

在第一个内链中,经过第n个BSN后,光子态变为

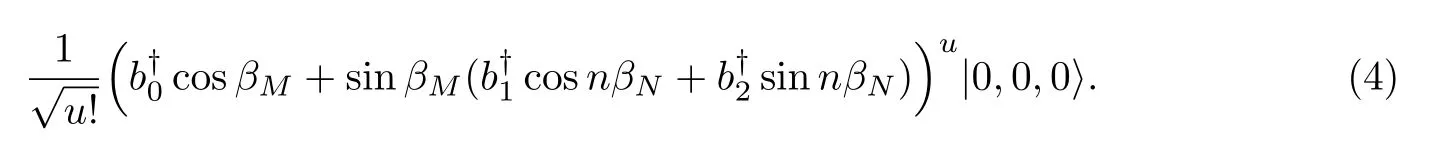
当n=N时,有

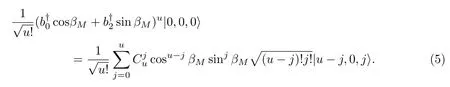
此时,D2会测量出现在区域2的光子.注意|u−j,0,j〉表示区域0有u−j个光子,区域1没有光子,而区域2有j个光子.因此,如果D2没有被触发,则意味着区域2中的光子数必然为0.相应地,光子的状态塌缩至

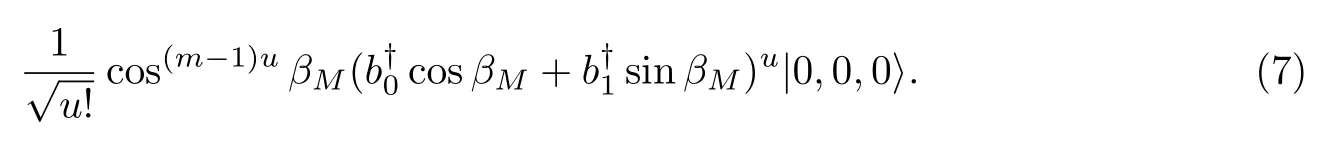
当m=M时,光子态变为

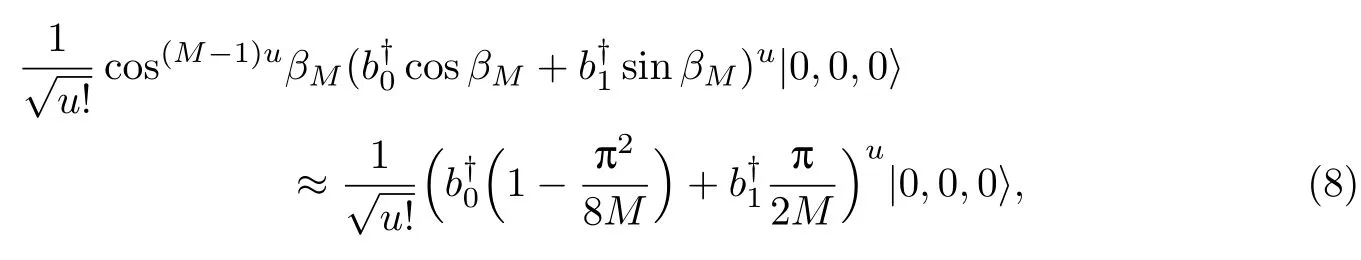
式(8)描述了调控结束时光子的状态,据此可以计算D0且只有D0找到光子的概率,

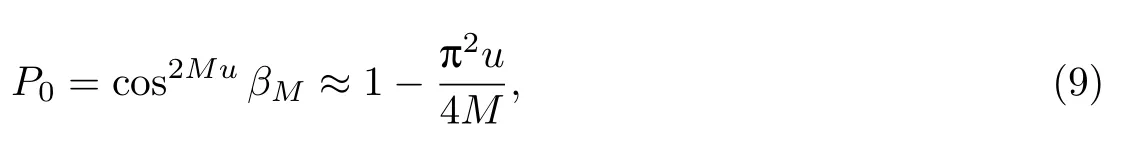
显然当M≫u时,P0可以无限趋于1.

情况2 SD为非透明.

如果第一个内链中的第一个SD没有找光子,则光子态塌缩至

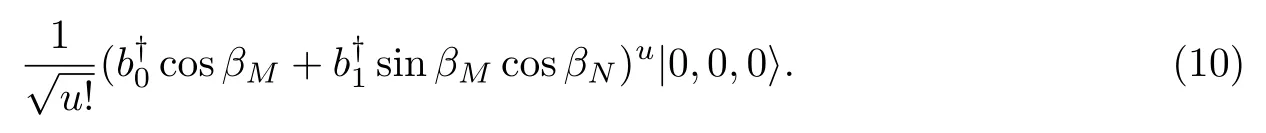
上述过程在第一个内链中重复N次,之后光子的路径叠加态将变为

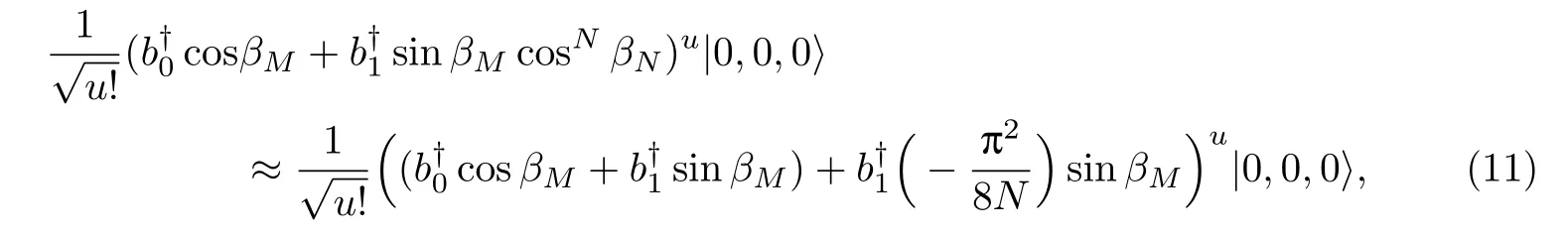
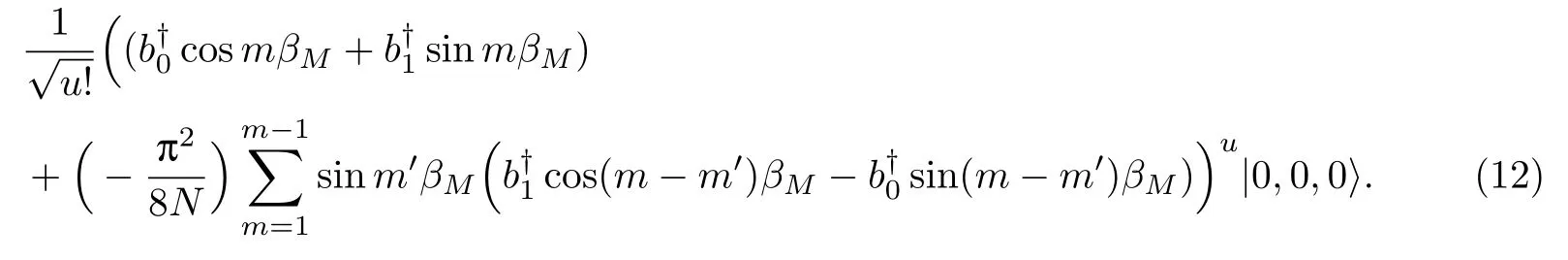
当m=M时,有

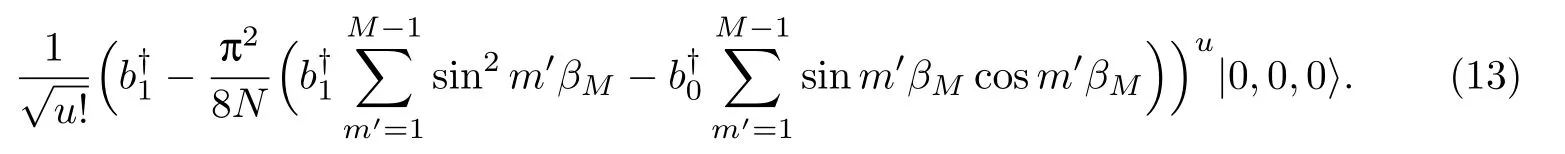
利用积分近似替代求和,即

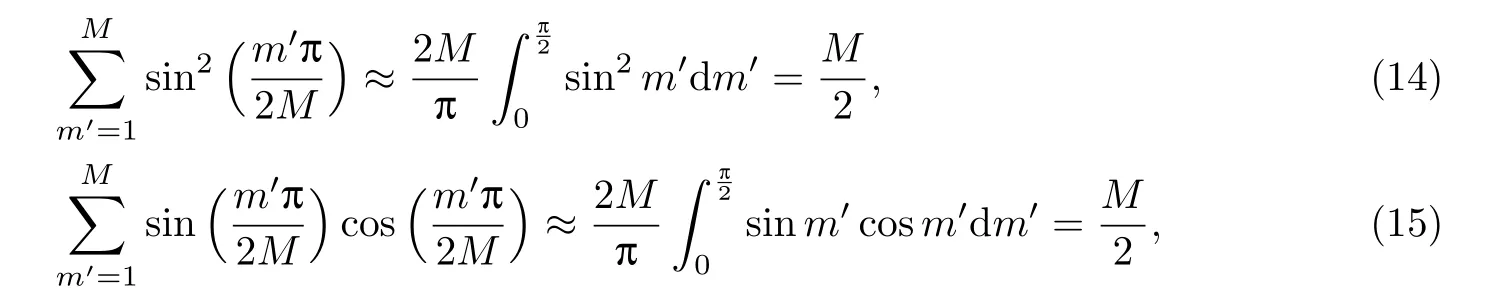
式(13)可近似写为

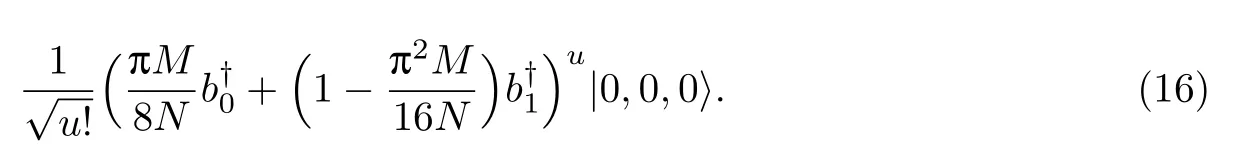
式(16)描述了SD非透明时,调控结束时光子的状态.通过式(16)计算D1且只有D1找到光子的概率P1.当N≫Mu,M≫1时,

在极限条件下,P1可以无限趋于1.

容易看出,D0或者D1触发代表光子正确感知到SD的状态,而非局域性的要求将通过以下方式来确认.以SD透明的情况为例,由于干涉作用,任意进入内链的光子最终都会导致D2的响应.因此D2的静默证明了在整个调控过程中区域1和区域2中都没有光子出现,因而光子和SD没有实际“接触”.与此同时,由于系统中的总光子数是守恒的,一旦所有的D2以及D1都没有找到光子,则意味着D0必然接收到所有的u个光子,对应的光子态为|u,0,0〉.换言之,实际上并不需要具体知道D2的探测结果,仅从D0自身的探测结果——是否接收了所有的光子,即可判断出光子是否和SD有任何“接触”.对于SD非透明的情况,分析是类似的.一旦D1接收到了u个光子(对应的光子态为|0,u,0〉),即可判断整个调控过程中没有SD被触发,这意味着没有任何光子会和SD相接触.综上所述,若有且仅有D0或D1被触发,即代表光子正确地被非局域操控了,而计算结果显示概率P0和P1可以同时趋近于1,这代表反事实量子调控方案的成功率可达到100%.

以上给出了反事实量子调控方法的具体数学描述和相应物理解释.需要说明的是,嵌套链式干涉仪结构是一个非常好的演示模型,但不是反事实量子调控实现的唯一模型.Salih等[5]给出了一个等效的迈克尔逊干涉仪模型.Aharonov等[14]将反事实量子调控理论拓展至物质波,该研究也将用于研究柴郡猫现象[15-17].然而,无论具体的模型为何,基本的数学过程都是类似的.另外,通过计算可以进一步探讨任意光源的反事实量子调控[13],目前已经证明,只要一个光脉冲的能量是有限的,它就可以被反事实地调控.

3 反事实量子调控的实验验证

由上述理论分析可以看到,反事实量子调控的实现需要大量串联的干涉仪,这给实验验证工作带来了很大的挑战[18-19].尽管困难重重,对于单光子的反事实量子调控的实验验证工作在2017年迎来了的重大突破.Cao等[20]和Liu等[21]相继独立完成了原理性实验验证.

Cao等[20]的实验中采用的是单光子光源和迈克尔逊干涉仪型的光路结构,此结构的优势在于不需要大量同一种状态的SD,从而一定程度上降低了光路的复杂性(但需要高速光开关).同时,为了应用此结构,路径干涉被偏振干涉所替代.另外,为了方便演示,实验中的SD被一个黑白的中国结所替代,黑和白代表了原本SD的两种状态.通过单光子一个个的累计成像,可以清楚地看到,这个中国结被很好地通过非局域的方式复现(见图3(b)).

Liu等[21]采用的则是Mach-Zehnder嵌套干涉仪链结构.实验中,外链采用了2个干涉仪,而内链中则实现了7个串联的干涉仪.但是在光源上并没有采用单光子源,而是采用了弱相干光源.由于相干光在不同路径的强度分布和单光子情况下的光子概率分布具有相同的数学形式,因此该实验在原理上验证了单光子反事实量子调控方案的正确性和可行性.然而需要说明的是,由于是强度分布,这意味着光子必然在SD处出现,这点在实验中也反映出.因此,该实验实现的并非是真正的反事实量子调控,只能称之为类反事实.尽管如此,该实验工作还是为后续的多光子反事实量子调控研究带来了启发.

在合适的条件下相干光源是可以实现真正的反事实量子调控的.事实上,和人们的预期不同,我们发现如果以传递信息为目的,较强的相干光源反而是必要的[13].这是因为弱相干光源(例如平均光子数小于1)会有很大概率不触发任何探测器,因而不能保障信息的有效传输.采用强相干光源带来的劣势是需要相比于单光子情况更多的干涉仪,这显然加大了实验的难度.为了解决这个问题,我们也对针对多光子反事实量子调控的实验可行性做了研究,并给出了一个修正方案.对于反事实量子调控来说,重点在于光子和SD没有接触,而对于D0和D1来说,并不需要将所有光子都集中到一个探测器上才能明确SD的状态,一定的光子分布即可以达到相同的效果.数值模拟结果显示,相比于现有的实验条件[21],修正方案仅需要通过改变BSM的透射率以及采用单光子探测器,就可以实现对平均光子数为200的相干脉冲的反事实量子调控的实验演示.

4 反事实量子现象的非局域性研究

尽管反事实量子调控理论可以通过严格计算光子的动力学演化过程而得到,但其展现出来的反直觉物理现象,还是引发了众多科学家的兴趣.Gisin等[22]尝试用经典图像来解释整个现象,其观点可以陈述为没有声音也是一种“声音”,并认为反事实量子直接通讯的核心是利用真空态来代表信息,而这在经典条件下也可以实现.但Hance等[23]明确指出:经典条件下只能反事实地传输0或者1,而无法完整传递一个比特的信息;反事实效应必然是量子的.

除了反事实效应是否是量子的这一问题,更多的争论聚焦于反事实量子现象的非局域性本身.除了Aharonov等[14]从物质波的角度对反事实量子理论做了重新阐述外,一些新的研究方法也被提出,并用于判定反事实量子调控的非局域性,例如历史一致理论[24]、Fisher信息法[25-27]以及弱迹判定法[28-30]等.需要说明的是,这些判据取决于不同的科学家对非局域性的不同解读和定义,因而它们并不是统一的,甚至被用于否定反事实量子调控的非局域性.同时需要强调,这些判据所遵守的计算法则依然都在量子力学框架之内,因而并不会产生任何的新物理内容.以弱迹判定法为例,研究人员希望通过引入额外的弱测量来判断当SD为透明时光子是否会出现在内链中(出现则反事实调控不是非局域的).注意,之前的论述是把整个内链视作为一个探测器来判断光子是否会出现在内链中的,即由于持续的干涉作用,任何进入内链的光子都会触发D2,因此D2没有触发则意味着没有光子进入内链.然而一旦额外的测量被引入内链,这毫无疑问会打断内链中的干涉过程,由此会造成一个非零的弱值.Vaidman等[28-29]认为这个非零弱值便是光子出现在内链的证据,从而否定非局域性的存在.事实上,早在2007年,Vaidman[31]便研究过类似的问题(三盒悖论),并得到了一个十分怪异的结论——“光子既没有进入干涉仪,也没有离开干涉仪,但是光子会出现在干涉仪中”,而判断的依据便是非零的弱值(在干涉仪的输入端和输出端的弱值为0,但在干涉仪内部的路径上,出现了非零弱值).这听上去并不合理,因此,2013年Li等[32]对此问题做了细致的计算和解释.研究表明,Vaidman得到的非零弱值确实来源于弱测量,但更合理的解释是——由弱测量引起的系统误差[32-33].注意到反事实量子调控的核心是不同序列的多重量子测量,而额外加入测量势必引起对原系统的干扰,这就像在杨氏双缝干涉实验中,通过测量来确认光子路径则必然会破坏光子的干涉.因此非零弱值并不能说明反事实量子调控不是非局域的.

5 基于反事实量子理论的应用性研究

除了针对反事实量子现象的物理本质研究,目前相关应用的研究也取得了丰厚的成果.按照SD所代表的客体的状态,这些研究可分成经典客体和量子客体两类,二者区别在于量子客体的状态可以是量子叠加态,即透明/非透明的量子叠加态.

5.1 经典客体

此类研究主要涉及量子通讯和量子探测,例如立足于保障信息安全的反事实量子保密通讯[34],替换多重测量为多重相位操作以提升通讯效率的准反事实量子通讯协议[35],要求多个孤立客体同时控制公开传输信道的反事实量子多方通讯[36],旨在保持成像精度的同时通过减少样本所受的辐照(来源于样本对于光子的吸收)从而降低样本的损伤的反事实量子鬼成像[37]以及用于隐蔽窃听者的反事实量子窃听[38-39]等.Hance等[37]的工作起源于基于无相互作用测量的成像研究[40-42].作为无相互作用测量的高级版本,反事实量子鬼成像显示了更好的信噪比和对样本更佳的保护[37].而Li等[39]给出的反事实量子木马窃听则是该课题组首次提出和研究的一种窃听方案.在传统的木马窃听方案中,窃取信息是通过发射额外的光场(或光子)进入被窃听设备,然后分析反射回来的光场(或光子)来进行的[43].但很明显,通过主动检测,非法的入射光子往往易被筛滤出来,因此传统的木马窃听方案是很容易暴露的.利用反事实量子调控,情况将会发生极大转变.在Li等[39]方案中,由于量子芝诺效应,针对窃听光子的探测只会使迫使该光子被局域在窃听装置内,即使用来探测的探测器是理想的.这使得木马攻击方案中的窃听光子是近乎隐形的,因而窃听极难暴露.与此同时,通过对光路的重新设计,结合多重相位调控的使用,该方案可以有效读出多种编译信号,具有很强的识别能力,因而对多种量子保密通讯协议都会产生威胁.Li等[39]具体分析了两种具有典型性的量子保密通讯协议的安全性[44-48],包括著名的量子直接保密通讯协议——Ping-Pong通讯协议[44],并首次证明该协议在理论上是有安全漏洞的.当然,对于窃听技术的研究,其最终目的还是为了升级现有通讯技术,保障通讯安全性.因此,Li等[39]的研究除了给出量子窃听方案,也讨论了可能的防御方法.研究结果显示,反事实量子木马攻击并不难防御,但是单纯地依靠主动检测非法入侵光子是行不通的.因此,目前针对传统木马攻击的防御策略都必须要进行升级更新.

最后还需要补充一点,现有的反事实量子木马窃听方案中采用的光源仍为单光子源.考虑到多光子光源远比单光子光源更容易制备和操控,应用多光子光源将极大地方便和扩展上述方案的实际应用.而利用Li等[13]的关于多光子反事实量子调控的研究成果,可以将上述窃听技术拓展到宏观领域从而实现在探测的同时无法被反追踪的隐蔽量子雷达,这在军事上是极有意义的.

5.2 量子客体

此种情况下用于操控光子的客体处于吸收光子/不吸收光子的量子叠加态,其具体的实现方式包括里德堡原子[49-50]、埋入原子的单边腔[51-53]等.该方向的研究工作由Guo等[54-55]首先展开,并已取得了众多重要结果.研究显示,量子客体和一个光子可以在没有任何物质粒子交换的情况下被远程地纠缠起来.这便是反事实量子纠缠产生,是一种新的纠缠产生方式.进行相关研究的还包括Chen等[56-57].Guo等[58]的研究表明,一个未知量子态可以反事实地在没有预制纠缠的条件下被远程传输,这实现了传统量子隐形传输[59-61]的功能.除了以上介绍的工作,基于反事实量子纠缠的研究成果还包括各种反事实量子逻辑门[62-64]、反事实量子克隆[65]、反事实量子贝尔态分析[66-67]等.而Li等[68-69]和Wang等[70]也在相关方向做了一系列的研究工作.研究人员理论研究了如何实现两个未知量子态的反事实交换,即实现非局域量子交换门[69].具体来说,两个未知量子态被分别独立制备在相距遥远的一个光子和一个原子上.交换之初,光子和原子之间没有纠缠.在交换过程中采取了多轮的反事实量子调控,而在每两轮非局域调控之间,对光子和原子进行独立的局域调控.这实际上建立了一种反馈机制[68],通过这种机制,该方案不仅允许原子调控光子的演化,同样也使得光子有能力对原子的动力学演化过程施加影响.最终,该方案实现了一种新型的、双向的量子隐形传输.有别于传统的量子隐形传输方案,该方案既不需要预先在两个通讯者之间分发纠缠粒子对,也不需要将最后的贝尔测量的结果在通讯双方之间传递,因此在整个传输过程中完全没有任何粒子在通讯双方之间交互,这可以说是真正的心灵传输方案.Li等[68-69]的研究还指出,反事实未知量子态交换是通过多重量子测量实现的.和传统的认知不同,这里的多重量子测量可以平滑、柔和地影响量子系统的演化.其作用可以近似地用一个幺正时间演化算符来描述.更重要的是,研究表明,任意的幺正时间演化算符都可以通过多重量子测量在特殊设计的光路下实现,这在理论上提供了一种普适的将局域量子调控转换为非局域量子调控的方法,从而为后续的非局域量子调控研究打开了新的局面.利用上述结论,后续的研究便是实现高维量子纠缠态的非局域制备[36].

6 结论与展望

本工作从无相互作用测量和量子芝诺效应出发,回顾了反事实量子调控理论的研究历史、具体概念、基础理论和相关的应用性研究.研究显示,多重量子测量可以平滑、柔和,但非局域地影响量子系统的演化.通过对反事实量子调控的研究,能更好地理解量子测量的作用和非局域性.在应用层面的研究结果也表明,反事实量子调控在量子通讯、量子计算和量子探测方面都有重要的应用价值.需要说明的是,从实际应用角度来说,由于多重量子测量的运用,相对于其他量子调控方式,反事实量子调控会需要更长的实现时间.另外,由于连续干涉过程的存在,反事实量子调控对于环境噪声是异常敏感的.因此,如何提高反事实量子调控的效率以及对环境噪声的鲁棒性,是未来相关研究中的重要一环.通过这类研究,能够大大扩展反事实量子调控的应用面,降低应用难度,更有助于真正实现对于宏观对象的非局域量子调控.