不确定时滞广义半马尔科夫跳变系统的随机稳定性研究

彭春源

（贵州民族大学 数据科学与信息工程学院，贵州 贵阳 550025）

1 研究目的和意义

广义半马尔科夫系统是一类特殊的随机切换系统，其切换过程由半马尔科夫链控制，主要用来为结构遭遇随机变化的实际工程建立模型。例如目标跟踪系统、容错系统和网络系统等，鉴于其在工程领域中的广泛应用，近几十年来越来越多的学者投入对广义半马尔科夫系统的研究中。对于任何系统，首先考虑的特性就是稳定性，关于稳定性的研究不仅对控制理论的发展起着重要的推动，也是实际工程领域中迫切需要解决的问题。例如李成群等[1]研究了一类具有时滞的随机中立型系统的稳定性，并得到了线性矩阵不等式形式的判别系统随机稳定的充分条件；马小康等[2]使用有别于线性矩阵不等式的方法研究了具有不确定时滞马尔科夫神经网络系统的稳定性。在跳变系统中，驻留时间是指系统跳变之后维持该模态的时间，当发生新的一次跳变之后其值从零开始。对于马尔科夫系统，由于驻留时间服从指数分布，所以转移率为常数，目前关于马尔科夫系统的研究是一个热门的领域，主要集中在稳定性、可达集和控制器设计等[3-4]。实际生活中，许多随机系统的驻留时间并不服从指数分布，这导致马尔科夫系统的应用受到极大的限制，因此如何把有关马尔科夫系统的研究成果推广到半马尔科夫系统显得尤为重要。另外时滞现象常出现在许多工程系统中，例如病毒传播模型[5]，是导致系统不稳定和功能衰减的主要原因。为了满足系统最基本的特点，有关时滞系统的稳定性研究已是一个经久不衰的热门领域[6]。伴随着科技的进步，MATLAB 中的LMI 工具箱能够有效解决线性矩阵不等式的可行解、最优解等问题[7]，以线性矩阵不等式的形式给出系统稳定性的判据不仅在理论上有着重要的作用，也给问题的数值求解带来极大的方便。

因此，文章以具有不确定时滞的广义半马尔科夫系统为研究对象，考虑驻留时间服从韦伯分布时系统的随机稳定性。

2 问题描述

文章研究一类具有时滞的广义半马尔科夫跳变系统的随机稳定性，系统的模型如下：

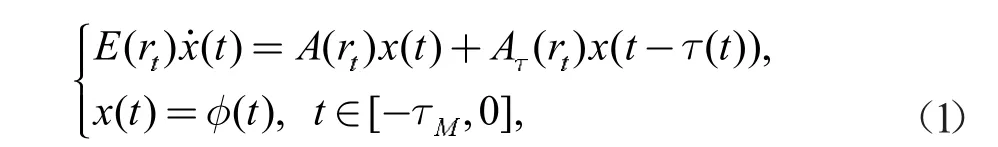
其中τ（t）是不确定时滞且满足

在式（2）中：τm，τM和μ 都是常数；x(t) ∊是系统的状态向量，E（rt），A（rt）和Aτ（rt）是实常数矩阵，在广义系统中，通常情况下矩阵E（rt）的秩rank（E（rt））＜n；{rt，t>0} 是右连续的半马尔科夫过程，其取值为δ={1，2，…，K}且转移概率满足下式：

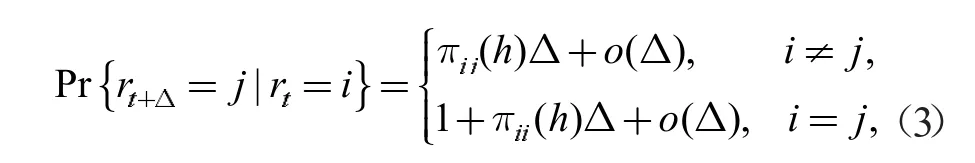
其中h>0 表示系统在模态跳变后所驻留的时间，当系统发生跳变的时候，h 的取值从0 开始；当i≠j时，πij（h）>0 为系统从模态i 到模态j 的转移率，i=j时，π（iih）=-π（ijh）＜0。为了符号的简练，对于任意的rt=i∈δ 时，使用i 代替rt，比如E（rt）写为Ei。

符号说明：I 表示单位矩阵，X>0（≥0）表示X 是实对称正定（半正定）矩阵，sym{A}表示矩阵A 加上它的转置AT，*表示对称块矩阵中的对称项，L 表示随机过程的弱无穷小算子，E 表示数学期望算子。

下面给出广义半马尔科夫跳变系统随机稳定性的定义和需要用到的引理。

定义1[8]：称系统（1）是正则的，如果对于任意i∈δ，都有det（sEi-Ai）不恒等于0。

定义2[8]：称系统（1）是无脉冲的，如果对于任意i∈δ，都有deg（det（sEi-Ai））=rank（Ei）。

定义3[8]：称系统（1）是随机稳定的，如果对于任意的初始条件φ（t）和r0∈δ，总存在一个正数M（φ（t），r0），使得系统（1）的解x（t）满足

3 随机稳定性

对于系统（1），我们可得如下的线性矩阵不等式形式的随机稳定性判据。

定理1：称系统（1）是随机稳定的，如果存在矩阵Xi>0（i∈δ），Q1>0，Q2>0，Q3>0 满足

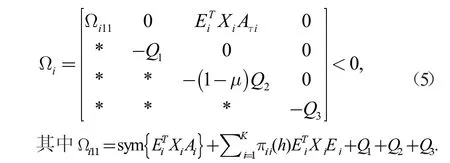
证明：对于广义系统，我们首先证明系统(1）是正则和无脉冲的。

根据Xi>0，可得

由（5）式得Ωi11＜0，注意到πij（h）>0（i≠j），Q1>0，Q2>0 和Q3>0，所以

接下来证明系统（1）是随机稳定的。

我们构造李雅普诺夫泛函V（x（t），rt）=V1（x（t），rt）+V2（x（t），rt），

其中

对构造的泛函进行弱无穷小运算，并联系式（3）给出的转移概率可得

联合式（5）、（8）和（9）得

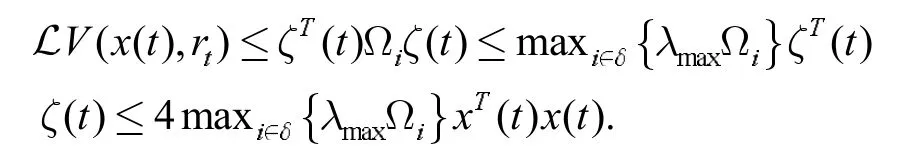
根据式（4），系统（1）是随机稳定的。证毕。

在式（5）中，由于πij（h）是与驻留时间h 有关的变化项，故无法利用线性矩阵不等式工具箱求解未知矩阵Xi（i∈δ），Q1，Q2和Q3。在文献[9-10]的启发下，当驻留时间服从韦伯分布的时候可有效解决此问题，韦伯分布的概率密度函数为

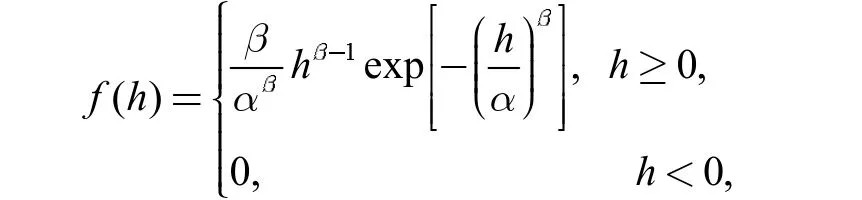
其中α>0，β>0 分别为韦伯分布的比例参数和形状参数，累积分布函数为

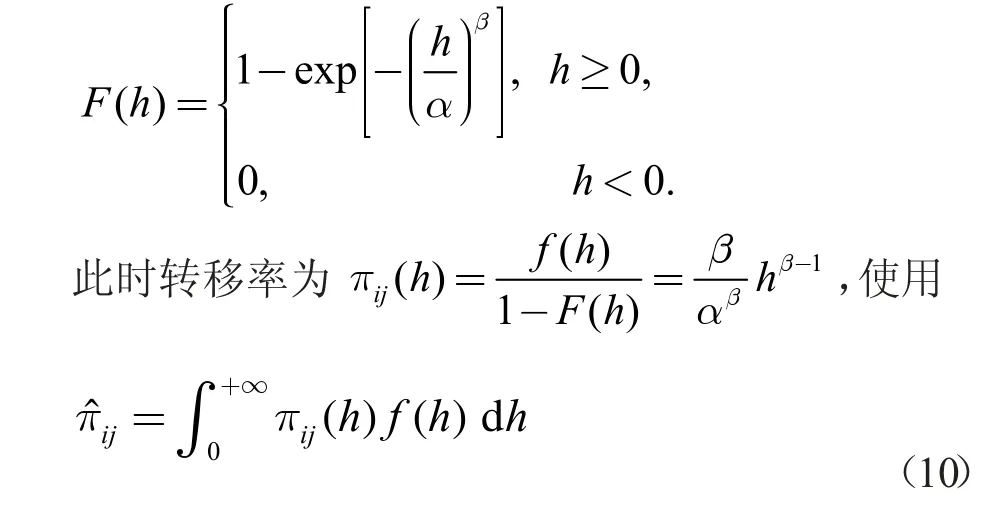
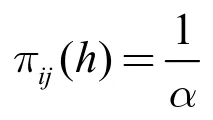
4 数值例子

这一节将列举一个例子来说明文章所得结果的有效性。

系统（1）的系数如下：

再利用MATLAB 中的Simulink 技术，系统（1）一种可能的模态跳变过程状见图1，相应的状态轨迹见图2，说明系统（1）是正则、无脉冲且随机稳定的，有效说明文章所得结果的正确性。

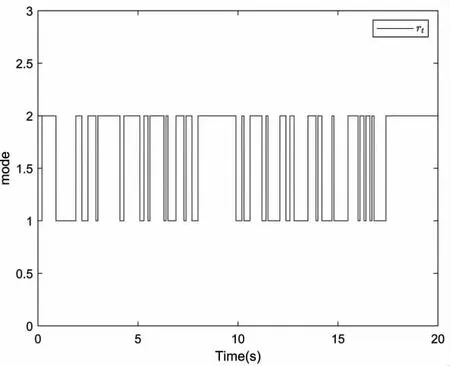
图1 模态跳变过程

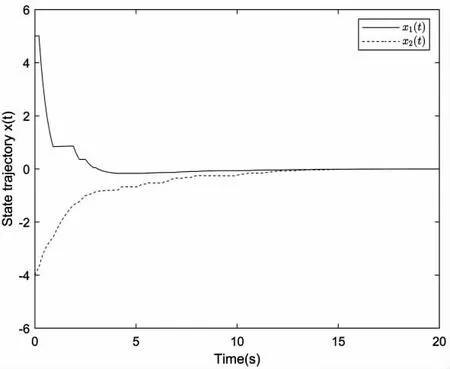
图2 系统状态轨迹