VTI 介质弹性波频率域多核并行正演模拟

岳晓鹏，付亚运，陈康靖

（许昌学院数理学院，河南 许昌 461000）

在地球内部广泛存在各向异性，如西非洲海岸、墨西哥湾及中国南海部分区域都存在各向异性地层，横向各向同性(TI)最为多见的，这种介质具有柱对称轴，对称轴在空间垂直的称为VTI 介质；对称轴在空间水平的称为和HTI 介质。正演是偏移和反演的基础，有限差分正演可以较准确地描述波传播规律，是波场正演时应用广泛的方法。频率域波动方程正演早期由Lysmer 等提出并利用该方法研究了波在各种介质中的特征；Jo 等人提出了减小数值频散的最优化9点格式[1]；Min 等提出了减小了空间采样点数的25 点差分格式；吴国忱教授用25 点差分格式正演了VTI和TTI 介质[2]，还有国内的诸多学者对于VTI 介质的数值模拟进行了研究[3-5]。

频率域正演优势在于没有时间累积误差[6]，每次用独立的频率正演，更适用于并行计算[7]。在并行计算研究方面，出现过很多的并行框架，GPU 并行、CPU 并行、集群并行等。很多框架设计结构繁杂，对开发人员要求很高[8，9]。

本研究在详细分析各种常见并行模式的基础上，设计了VTI 介质多核并行计算方法。与CPU 串行算法相比，具有较好的加速比。

1 VTI 介质频率域25 点格式

对于二维VTI 介质质频率域波方程如下

在式(1)中所有项，利用25 点格式离散时所需的点分布见图1。

ρω2U 系数见图1(a)，表达式为

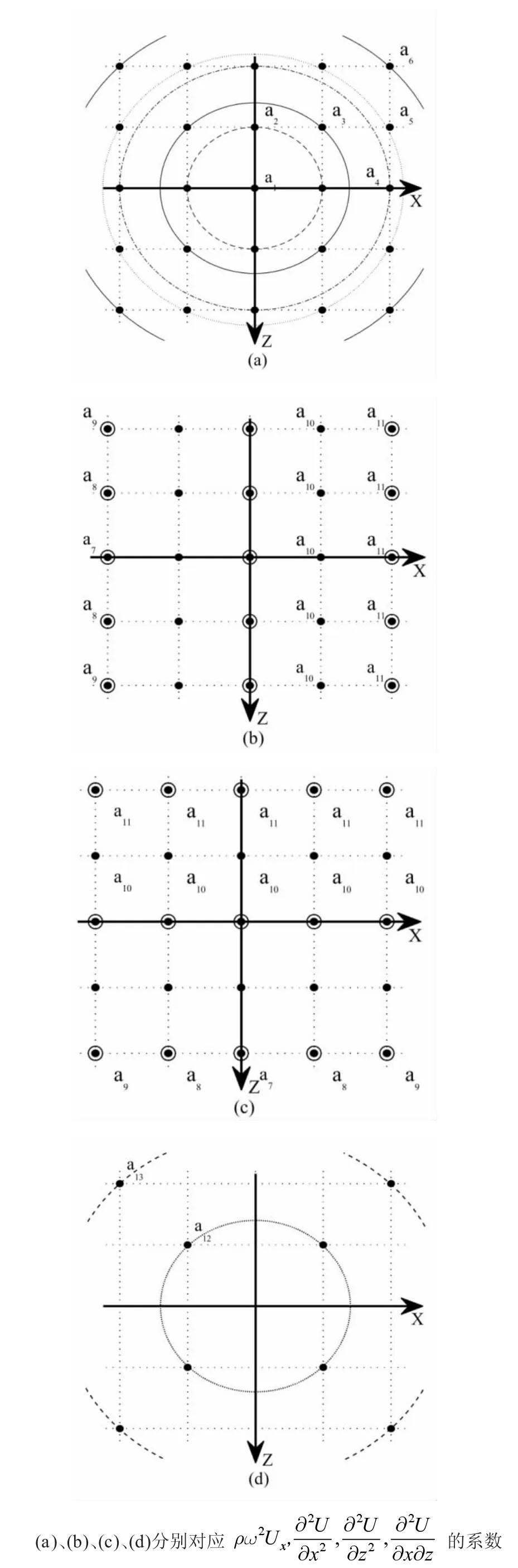
图1 25 点加权离散示意图

同理，可以展开其它几项，将所有算子带入公式(1)并进行整理后，可以得到矩阵方程

如果网格为N2×Nx，N=Nz×Nx，A 为2N 阶矩阵，Y是未知2N×1 矩阵，F 是2N×1 矩阵。

2 数值算例

地质模型为:纵波为4 000 m/s；横波2 000 m/s；介 质 2 500 kg/m3；NX=160，NZ=160； 空 间 步 长Δx=Δz=5 m，ε=0.5，δ=0.1。边界是PML 边界。记录时间0.3 s，采样间隔0.001 s，震源是Richer 子波，主频25 Hz，检波器在地表按网格排列，震源坐标为(80，80)，检波点坐标(100，100)，图2 和图3 为数值模拟的波场快照和地震记录。

图2 VTI 介质的波场快照（125 ms 时刻）

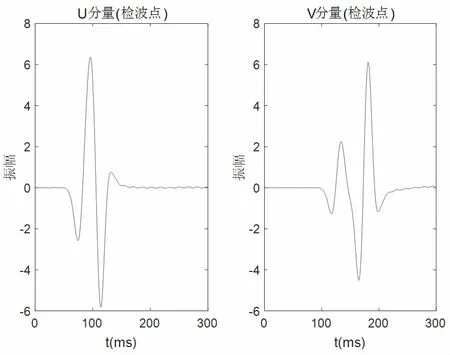
图3 VTI 介质的地震记录

3 多核并行正演对比分析

这里采用的多核并行方式是使用Matlab 的多核并行方法。正演模拟时使用的平台为双路Xeon E5-2650 v4，32 GB 内存的服务器，共有24 个计算核心。程序运行的主要耗时在矩阵方程(6)的求解上，例如当网格数为160*160 时，矩阵A就是一个80 000 阶（200*200*2）的大型稀疏矩阵，求解这样系数的矩阵方程相当耗费时间。对于VTI 介质频率域方程，可以采用并行的方式在每个频点独立求解。

假设计算网格数分别为100*100、130*130、160*160，190*190、220*220，四周加上PML 边界后，实际计算网格数为140*140、170*170、200*200，230*230、260*260，对比顺序执行和并行求解方程(6)平均耗时及程序运行时间，见表1。

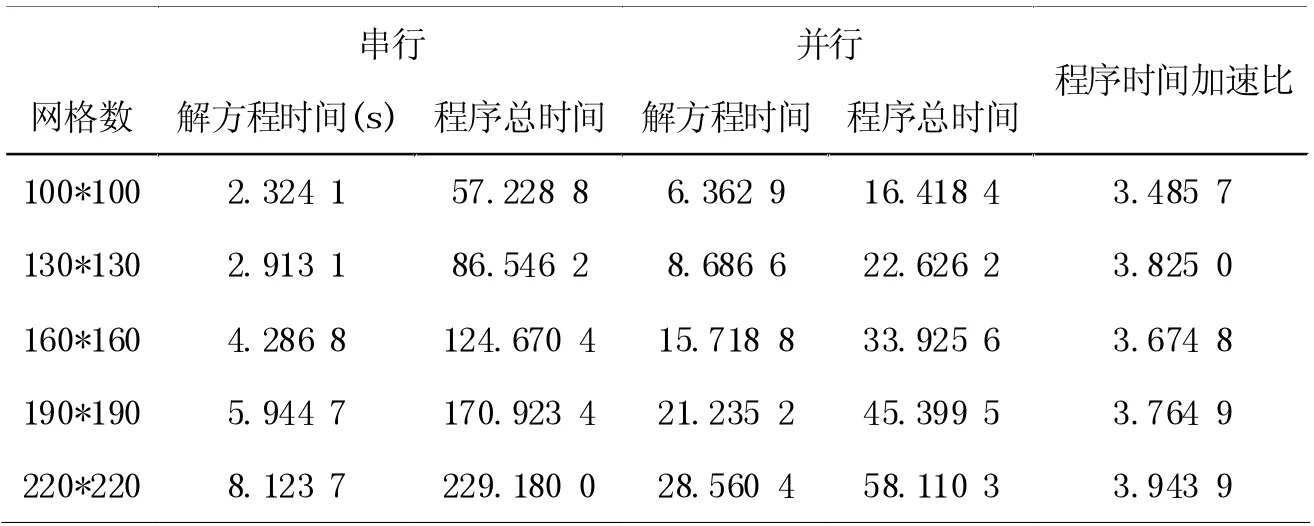
表1 两种方法耗时对比

为了更直观的说明问题，将以上数据作图表示，见图4。

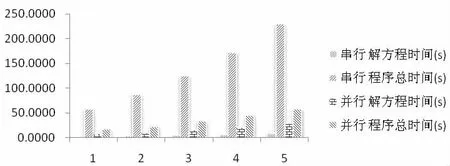
图4 两种方法耗时对比

4 结论

目前，CPU 正在朝着多核心方向快速发展，最新的i9-13900k 已经是24 核32 线程，然而，现有的波动方程正演及偏移成像代码大多是采用MPI 技术实现并行，这种进程级粒度的计算方式在集群之类的分布式系统上效果很好，在单个计算节点又要受到内存等限制，只能利用少数的计算核心，不能发挥多核处理器的最大效能。本研究将占据波动方程频率正演模拟主要计算时间的大型矩阵方程求解过程分配给多个计算核心，利用多核心并行计算方法，多个频点的求解过程可以同步计算完毕，即在进程中实现多核心并行，有效提高了多核处理器的利用效率和代码执行速度。