自动化分拣仓库中多自动导引小车在线协同调度算法

余娜娜，李铁克，王柏琳+

(1.北京科技大学 经济管理学院，北京 100083；2.钢铁生产制造执行系统技术教育部工程研究中心，北京 100083)

0 引言

随着电商行业的飞速发展，亚马逊、京东和顺丰等致力于打造智慧物流的互联网公司和物流公司纷纷建立了自动化分拣仓库，以实现高效、准确和快速的物流运作。自动化分拣仓库能够针对包装好的包裹，以其收货地址为分类标准，使用自动导引小车(Automated Guided Vehicle，AGV)实现包裹的自动分拣。自动化分拣仓库系统是一类典型的离散事件动态系统(Discrete Event Dynamic System, DEDS)，如何针对包裹动态到达的情况对多个AGV进行在线协同调度，是仓库系统高质量稳定运行的关键所在。

多AGV协同调度问题是指在AGV装载能力和搬运任务优先级等特定约束下，调度一组AGV来完成包裹的取货和送货等搬运任务，是对多AGV任务指派和路径规划的协同优化[1]。根据调度时获取搬运任务信息的完备程度，可将多AGV协同调度问题分为离线调度和在线调度两类[2]。针对离线环境下的多AGV协同调度问题，SAIDI-MEHRABAD等[3]提出一种两阶段蚁群算法，其中第一阶段解决AGV任务指派，第二阶段解决AGV无冲突路径选择；YANG等[4]提出一种双层遗传算法，其中上层解决AGV任务指派问题，下层解决AGV路径规划问题；LYU等[5]提出一种融合Dijkstra算法的遗传算法，该算法将基于时间窗的Dijkstra算法嵌入到遗传算法中，搜索最短路径并解决多AGV间的冲突。由已有文献可以看出，为保证求解质量，离线调度问题多采用集中决策策略，即中央控制系统提前根据所有已知信息为AGV确定最优的任务指派方案和搬运路径，并解决多AGV之间的碰撞和冲突，AGV仅负责执行调度方案，按照规划好的路线和时间窗行驶，不具备自动调整能力[6-7]。该方法虽然具有全局优化能力，但随着包裹和AGV数量的增加，集中决策的计算时间呈指数级增长，不能满足在线调度对系统即时响应的要求，且灵活性较差，无法快速应对动态环境下难以避免的AGV实时冲突与拥堵。

关于在线环境下多AGV的调度优化问题，已有研究多是针对任务指派或路径规划单个子问题进行优化。针对在线环境下的任务指派问题，已有研究提出了多种基于启发式规则的指派方法，如肖海宁等[8-9]提出一种实时多属性任务指派方法并证明了所提方法的有效性；CHAWLA等[10]提出多种指派规则,并通过仿真实验对不同规则的求解效果进行了评价；HO等[11]提出一种多属性的系统状态评估方法，并根据系统状态为AGV指派合适的搬运任务；此外，也有不少学者运用神经网络等机器学习算法来对指派规则进行在线优化或实时生成，如HEGER等[12]通过神经网络获得指派规则间最佳的组合方式；BO等[13]运用卷积神经网络对指派规则进行在线优化；CHOE等[14]运用在线偏好学习算法来对指派规则进行在线学习；SHIUE等[15]和HU等[16]运用强化学习方法从规则库里实时选择最优的指派规则。但这些文献均假设AGV按照最短路径进行搬运且搬运过程中不会发生冲突，即所提方法仅能优化多AGV任务指派问题，无法解决多AGV的无冲突路径规划问题。关于在线环境下多AGV的无冲突路径规划问题，已有研究多采用分散决策策略，即由AGV根据自身及周边的交通信息来自主规划搬运路径。如张丹露等[17]运用改进的A*算法预约表和动态加权地图，实现了多AGV的动态路径规划；YANG等[18]将改进A*算法和时间窗算法结合起来，提出一种层次规划算法实现了多AGV实时路径规划。这些文献虽然对多AGV间的冲突问题给出了解决方法，但所提方法无法对任务指派进行优化，此外，分散决策策略虽然可以保障系统运行的实时性和灵活性，但不能确保AGV的搬运路径是最优的。

由上述文献可见，关于多AGV任务指派和路径规划的协同调度问题，已有文献都是在离线环境下展开研究的，没有考虑实时在线的动态环境，无法满足在线调度对系统即时响应的要求；关于在线环境下多AGV的调度优化问题，已有文献多是针对任务指派或路径规划单个子问题进行研究，所提方法也仅能对任务指派和路径规划进行单独优化，无法实现二者的协同优化。在自动化分拣仓库中，AGV任务指派与路径规划是关系到系统高效运行的关键与核心问题，并且是紧密联系，互相影响的，单独优化任务指派或路径规划只能达到局部优化的效果，因此有必要建立一种多AGV任务指派与路径规划的集成模型和求解算法来实现多AGV任务指派和路径规划的协同优化。鉴于此，本文针对自动化分拣仓库中包裹动态到达的作业环境，以加权总搬运完成时间最小为优化目标，对多AGV在线协同调度问题展开研究，首先建立了问题的混合整数线性规划模型，然后针对问题特征提出一种多AGV在线协同调度算法(Multi-AGV Online Collaborative Scheduling Algorithm，MAOCSA)。算法通过集中决策对自动化分拣仓库及到达包裹的全局信息进行集中管理和调配，根据AGV的需要为其提供实时、准确的全局信息，并基于分散决策思想，将AGV视为具有自主决策能力的智能体(Agent)，基于实时的仓库信息自主确定搬运任务和行走路径。该算法结合了集中决策和分散决策的优势，可以实现多AGV任务指派和路径规划的协同优化，并且易于实现，能保障系统运行的实时性和灵活性。

1 问题描述与建模

本文借鉴文献[17]中的仓库模型，提出一类典型的自动化分拣仓库模型，其栅格地图如图1所示，主要包括以下部分：①分拣台，用于放置已经打包完成的包裹；②道路，图1中的白色栅格，用于AGV的行走，为了在最大程度上减少冲突和死锁的发生，降低交通管理难度，本文采用单向导引路径网络(Unidirectional Guide-path Network，UGN)[17]，即AGV在每条路径上只允许单方向行驶，且相邻两条路径的方向相反，每条路径可以允许行驶的方向在图下方和右方用箭头表示；③AGV，以一定的速度在仓库中行走并搬运包裹；④包裹投递区，根据包裹的收货地址，在地图上均匀地分割出多个投递区，每个投递区垂直向下的区域有一个容量有限的缓存区，当缓存区的包裹量达到上限时将其运出仓库进行装车发运；⑤包裹目的地，与包裹投递区相对应，若包裹投递区为1，则AGV需行驶至编号为1的栅格进行投递；⑥停靠区，所有AGV从停靠区出发，当所有包裹被搬运完成后返回停靠区。

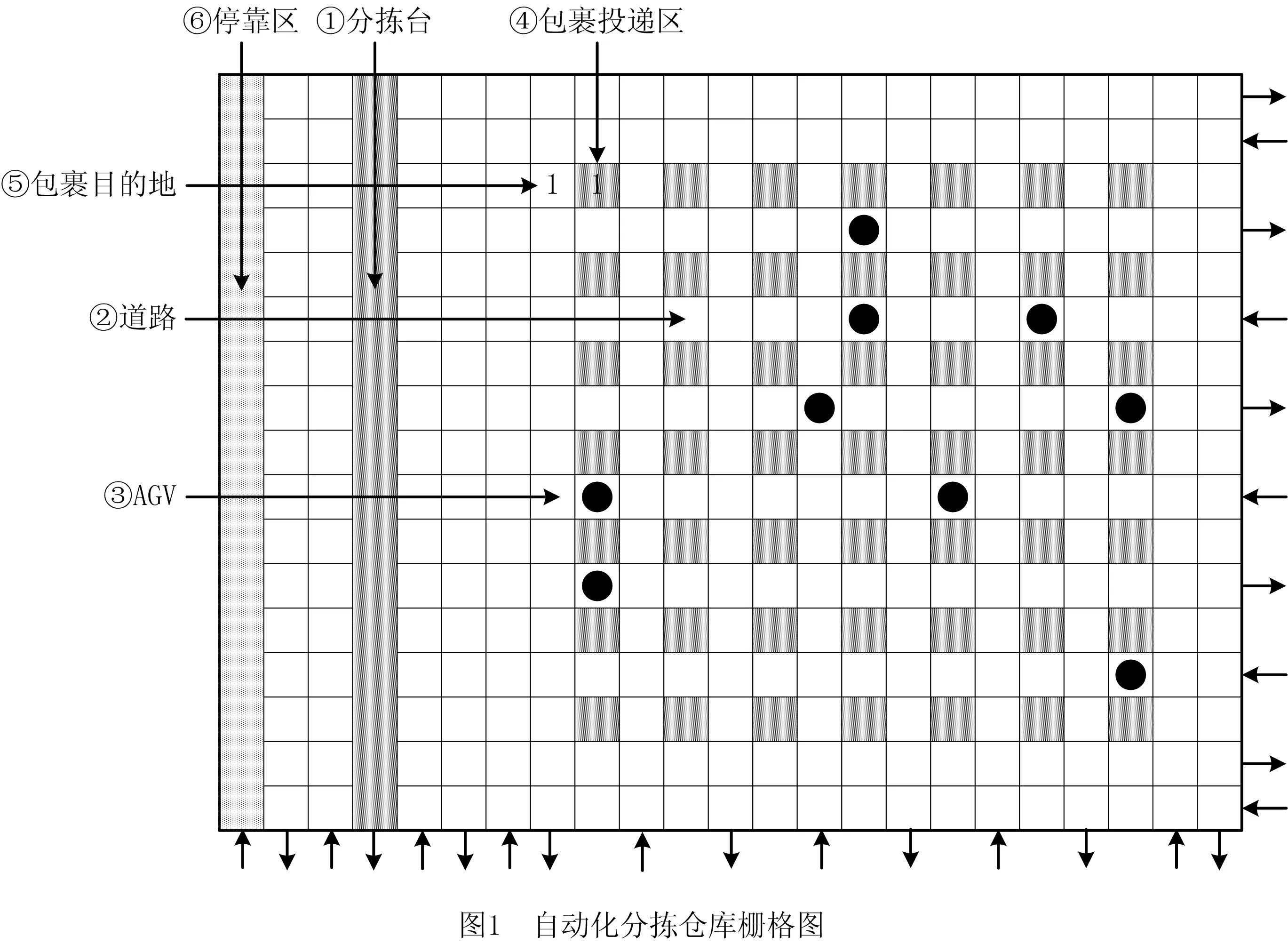
自动化分拣仓库中多AGV在线协同调度问题描述如下：①包裹动态到达，决策者只能对当前时刻已到达的包裹进行调度，未到达包裹的信息是未知的；②每个AGV单次只能搬运一个包裹，且每个包裹只能被一个AGV搬运；③包裹紧急程度不同，即包裹具有不同的优先因子(权重)；④优化目标为最小化加权总搬运完成时间。此目标与包裹的优先因子和搬运完成时间相关，其中搬运完成时间取决于搬运开始时间和搬运包裹的负载时间。虽然所有AGV在装载能力和行驶速度等方面是同质的，但每个AGV所处的栅格位置不同，且随着移动而动态变化，因此对于分拣台上待搬运的包裹，不同AGV在不同时刻，其与包裹的位置距离是不同的，这就意味着不同AGV在取运包裹时会产生不同的空载时间，进而产生不同的搬运开始时间和搬运完成时间。此外，AGV取包裹的空载时间和搬运包裹的负载时间均与AGV所选择的搬运路径相关，即目标值由任务指派方案和路径规划方案共同决定，有必要对AGV的任务指派和路径规划进行协同优化。

不失一般性，提出如下假设：

(1)所有AGV在零时刻可用；

(2)AGV运行过程中保持匀速，通过一个栅格所需的时间为1；

(3)AGV可横向或纵向跨越栅格，不允许沿对角线方向跨越栅格；

(4)AGV的装载和卸载时间极短，可忽略不计，即AGV的装载和卸载时间为0；

(5)不考虑包裹被卸载至投递区后的出库过程。

为便于描述，定义以下符号：

(4)目标函数。CT为加权总搬运完成时间。

自动化分拣仓库中多AGV在线协同调度问题的混合整数线性规划模型如下：

(1)

s.t.

(2)

(3)

j∈J,h∈G,t∈T{|T|-1,|T|}，

(4)

(5)

(6)

(7)

(8)

(9)

(10)

(11)

(12)

(13)

(14)

(15)

(16)

(17)

xjght={0,1},j∈J,(g,h)∈R,t∈T{|T|}；

(18)

(19)

(20)

(21)

2 多AGV在线协同调度算法

对于本文问题，若将n个包裹视为n个工件，m个AGV视为m个并行机，则在搬运路径确定的情况下，问题等价于带释放时间和顺序相关准备时间的并行机调度，具有强NP-难特性[19]，因此，本文问题也是强NP-难的，精确算法无法在有限时间内获得问题的解，不能满足实际应用需求。因此，本文基于分散决策思想，并结合集中决策的优势，提出了MAOCSA算法。

集中决策策略是AGV离线调度时较为常用的优化策略，即充分利用所有已知信息为AGV确定最优的任务指派方案和搬运路径，并解决多AGV之间的碰撞和冲突，具有全局优化能力。针对实时在线的动态环境，MAOCSA算法以各AGV的分散决策为主，但为了避免分散决策中信息采集的片段性和局部性，增强多AGV的全局优化能力，在算法中引入集中决策对自动化分拣仓库及到达包裹的全局信息进行集中管理和调配，并根据AGV的需要为其提供实时、准确的全局信息，以支持其实现优质的分散决策。其中全局信息包括当前时刻的待搬运包裹集、待搬运包裹集中的包裹属性信息(优先因子、到达时间、到达的分拣台、包裹目的地)、所有AGV的状态信息(工作或空闲)、所有AGV的位置信息(2.2节预约表)以及仓库系统的交通拥堵信息(2.2节栅格阻塞地图)。

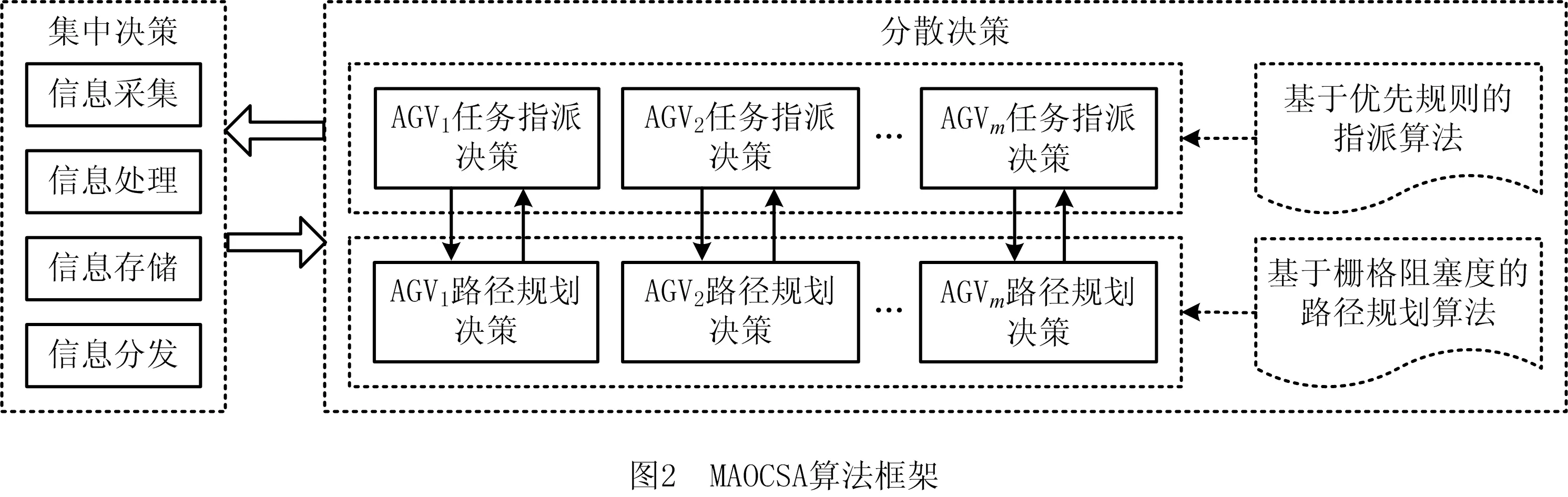
MAOCSA算法的求解思想为：一方面，中央控制系统通过集中决策方式对自动化分拣仓库及到达包裹的全局信息进行集中管理和调配，并根据AGV的需要为其提供实时、准确的全局信息；另一方面，基于分散决策的思想，将每个AGV视为一个可以自主决策的智能体(Agent)，它可以根据获得的实时数据信息进行个体决策。为支持AGV决策，在MAOCSA中设计了基于优先规则的指派算法和基于栅格阻塞度的路径规划算法。在AGV的决策过程中，既要考虑与其他AGV以及仓库全局运行状态的协同，也要考虑自身任务指派和路径规划的协同决策。为了实现与其他AGV和仓库全局运行状态的协同，每个AGV在决策过程中以仓库全局信息为依据做出优质的个体决策；为了实现自身任务指派和路径规划的协同决策，当其为空闲状态时，调用指派算法选择合适的搬运包裹，在作指派决策的过程中用到的空载时间等指标需调用路径规划算法确定，确定搬运任务后，调用路径规划算法为其规划搬运路径并解决与其他AGV间的冲突和拥堵，搬运完成后再调用指派算法重新选择搬运任务。由此可见，指派决策与路径规划决策同时进行，并且会根据仓库实时情况进行及时调整，因此可以达到多AGV任务指派和路径规划的协同优化。MAOCSA算法框架如图2所示。

2.1 基于优先规则的指派算法

本节提出一种基于优先规则的指派算法解决多AGV的任务指派问题，该算法以单个AGV为决策个体，每个空闲AGV都可以自主调用该算法选择合适的搬运包裹。针对t时间周期的仓库状态，令Iw表示待搬运的包裹集合，AGVd表示当前时刻需要进行指派决策的空闲AGV，Jf表示当前时刻处在空闲状态的AGV集合(AGVd∈Jf)，fij表示包裹Iw(i)与Jf(j)之间的规则指标值，集合记为F，则基于优先规则的指派算法具体步骤如下：

步骤2根据选定的指派规则，针对Iw和Jf计算指标值集合F。

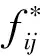
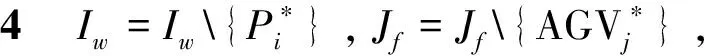
步骤5算法结束，输出AGVd的指派方案。

需要注意的是，基于优先规则的指派算法是一个通用算法，算法步骤2可以调用任意合理的指派规则，指派规则一旦选定，算法将执行此规则生成指派方案，并进入路径规划进行协同优化，实现在线协同调度。但是，不同规则在引入此算法后生成的方案质量并不相同，有必要在保证在线协同调度可行性的基础上进一步研发高质量的指派规则，因此本节根据问题特征提出分层规则和求和规则两种组合式指派规则。

分层规则记为RO(RI)，其中RO和RI为不同的指派规则，运算时先调用外层规则RO确定指标值，若存在多个指标值最优的方案，则进一步调用内层规则RI。分层规则生成指标值集合F的伪代码如下：

Input:Iw,Jf;

Fori=1 to|Iw|do

Forj=1 to|Jf|do

End For

End For

End For

ElseF=Fo;

Output:F

求和规则是将两种单一规则的表达式进行求和处理，由于不同规则指标值具有不同的数量级，本节并未采用简单的相加方式进行求和，而是首先对规则指标值进行极差标准化处理。令RB和RC表示求和规则包含的两种单一规则的指标值，R′B和R′C为极差标准化处理得到的指标值，则求和规则生成指标值集合F的伪代码如下：

Input:Iw,Jf;

F=∅;

Fori=1 to|Iw|do

Forj=1 to|Jf|do

R′B=(RB(Iw(i),Jf(j))-RBmin)/(RBmax-RBmin)//对RB进行极差标准化处理

R′C=(RC(Iw(i),Jf(j))-RCmin)/(RCmax-RCmin)//对RC进行极差标准化处理

fij=R′B+R′C;//两种单一规则指标值求和

F=F∪{fij};

End For

End For

Output:F

2.2 基于栅格阻塞度的路径规划算法

当AGV被分配搬运任务(包裹)后，即刻从当前位置行驶至该包裹所在的分拣台，取出包裹后运送至对应的包裹投递区进行投递，而后AGV立即更新为空闲状态，可以执行新的搬运任务。在搬运投递过程中，如何为AGV进行路径规划，在避免多AGV间的冲突和拥堵的前提下加快作业效率，这是问题优化的关键和难点。因此，本节提出一种基于栅格阻塞度的路径规划算法，该算法以单个AGV为决策个体，各AGV都可以自主调用该算法规划搬运路径，并且能有效解决与其他AGV间的冲突和拥堵，具体方法如下。

(1)多AGV间冲突的解决

多AGV间的冲突有节点冲突、相向冲突和追击冲突[17]。由于本文为UGN路径网络，且AGV为匀速行驶，可避免相向冲突和追击冲突，因此本节重点考虑AGV间的节点冲突。为了避免发生节点冲突，定义预约表来记录每个栅格的占用状态。预约表是一个同栅格地图行列相等的二维表格，若某栅格被一个AGV所占用，则预约表中该栅格位置则会记录该AGV编号。预约表的更新周期为Δt，并存储从t-ns·Δt～t时段的历史预约表。AGV每移动一个栅格均需查看当前周期的预约表，若多个AGV在某一时刻均向同一栅格移动，发生节点冲突，则以AGV优先级决定进入栅格的顺序，优先级最高的AGV优先占用该栅格，其他AGV需停车等待。根据包裹的紧急程度等因素，设计如下冲突AGV优先级规则：

规则1为Jc中搬运包裹优先因子高的AGV赋予高优先级，其中Jc表示发生节点冲突的AGV集合。

规则2若不满足规则1，即存在多个AGV的搬运包裹优先因子相等，则计算Jc中各AGV造成的拥堵规模，即若该AGV停车等待，则必须随之停车等待的AGV个数，为造成拥堵规模大的AGV赋予高优先级。

规则3若不满足规则1和规则2，则计算Jc中各AGV在当前搬运任务中的拥堵时间，即该AGV在搬运当前包裹的过程中累计停车等待时间，为拥堵时间长的AGV赋予高优先级。

规则4若不满足规则1～规则3，则计算Jc中各AGV当前搬运任务的预计搬运完成时间，即不考虑冲突和拥堵情况下的期望搬运完成时间，为预计搬运完成时间小的AGV赋予高优先级。

规则5若不满足以上4条规则，则随机决定冲突AGV的优先级。

(2)多AGV间交通拥堵的解决

为了解决交通拥堵问题，首先提出栅格阻塞地图(Grid Blocking Map, GBM)来记录每个栅格的拥堵程度。栅格阻塞地图是一个同栅格地图行列相等的二维表格，每个位置记录相应栅格在当前时刻的栅格阻塞度(Grid Blocking Degree, GBD)。式(22)为栅格g在t时间周期的栅格阻塞度GBDgt的计算公式:

(22)

式中:Ng表示在交通顺畅(不考虑冲突)的情况下，从t-ns·Δt～t时间周期栅格g应该通过的AGV数量估测值，通过历史预约表获得；H(j)的表达式见式(23):

(23)

其中tjb表示第j个AGV在t-ns·Δt～t时段为了通过栅格g而产生的等待时间。

针对AGV路径规划问题，应用较为广泛的是A*算法[20]，但A*算法中没有考虑实时的交通拥堵情况，当AGV数量较多时，极易造成AGV间不必要的拥堵，进而降低搬运效率。因此本文将GBD引入传统A*算法中，提出一种改进A*算法，定义了式(24)来表示栅格g的路径代价:

f(g)=l(g)+h′(g)。

(24)

式中：l(g)表示从起始栅格到当前栅格的路径代价，为已执行的真实值；h′(g)表示从当前栅格到目标栅格的路径代价，为预测的估算值，包括从当前栅格到目标栅格的估算行走时间h(g)和估算拥堵时间GBDgt，即h′(g)=h(g)+GBDgt。

多AGV间交通拥堵的解决主要包括两方面：首先，在AGV获得新的搬运任务时，运用改进A*算法为其规划初始搬运路径，以此减少拥堵情况发生的概率；另外，在AGV搬运过程中，根据当前时刻的交通拥堵情况对搬运路径进行动态更新，以此减少因交通拥堵而产生的等待时间。

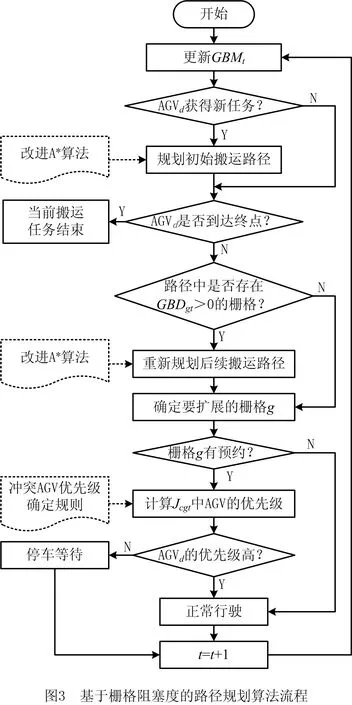
综合上述分析，基于栅格阻塞度的路径规划算法流程如图3所示，其中GBMt表示第t时间周期的栅格阻塞地图，Jcgt表示第t时间周期在栅格g发生节点冲突的AGV集合。

2.3 多AGV在线协同调度算法步骤

针对以上算法设计，令Ic表示已经完成搬运的包裹集合，终止条件为|Ic|≥n，则多AGV在线协同调度算法的具体步骤如下：

步骤1初始化t、Iw、Ic、Jf和GBMt。

步骤2若(Iw≠∅)∩(AGVd∈Jf)，转步骤3，否则转步骤5。

步骤3运用2.1节基于优先规则的指派算法为AGVd做指派决策，若AGVd获得搬运任务，转步骤4，否则转步骤5。

步骤4运用2.2节的改进A*算法，为AGVd规划初始搬运路径。

步骤5运用2.2节基于栅格阻塞度的路径规划算法，解决AGVd与其他AGV间的冲突和拥堵。

步骤6t=t+1，更新Iw、Ic、Jf和GBMt。

步骤7若满足终止条件|Ic|≥n，则算法结束，输出调度解和目标函数值，否则转步骤2。

3 仿真实验

3.1 实验设计

本节首先对不同指派规则的求解效果进行了对比和分析，然后对MAOCSA算法的有效性进行了验证。实验中所有算法均采用MATLAB编程实现，运行环境为Intel(R)Core(TM)i5-8250U/CPU 1.60 GHz 1.80 GHz/8.0 GB/MATLAB R2014a。以图1所示的自动化分拣仓库模型为仿真实例，展开仿真实验。仓库规模设置为：|G|=391，|GI|=17，|GP|=17，|GD|=49；算法参数设置为ns=6，Δt=1；包裹分为紧急、重要和普通3类，对应的优先因子分别为w=1, 0.5, 0.2；问题规模n=500, 1000, 2000, 3000，m=5, 10, 15，根据问题规模将实验分为12组，每组随机生成10个算例，算例中AGV的初始栅格、包裹所在的分拣台栅格和目的地栅格在GI、GP和GD中均匀随机产生，其他算例参数设置为：wi∈DU{1,0.5,0.2}，ri∈DU[1,30n/m](单位：s)，其中DU[a1,a2]为位于[a1,a2]的离散均匀分布。

3.2 指派规则的对比分析实验

首先采用相对偏离率(Percentage Relative Difference，PRD)来衡量6种单一规则求解效果的差异，包括文献[17]中提出的最短空载时间优先规则(Shortest AGV No-load Time，SANT)、文献[19]中提出的最早到达时间优先规则(Earliest Release Time，ERT)、最短负载时间优先规则(Shortest AGV Load Time，SALT)、最短总搬运时间优先规则(Shortest Total Processing Time，STPT)、最长总搬运时间优先规则(Longest Total Processing Time，LTPT)以及本文根据问题特征设计的最高优先因子优先规则(Highest Priority，HP)。PRD的计算公式如式(25):

(25)

其中:CT(A)为规则A取得的目标值，CT*为6种规则取得的CT最小值。

6种规则的PRD均值和标准差如表1所示。本节运用方差分析(Analysis of Variance，ANOVA)对每组实验进行PRD均值差异性的显著性检验，假设α=0.05，对应的F临界值为2.39。表1的最后两列给出了每组实验的F和P值。

根据表1可得：①6种规则的求解效果排序为HP>SANT >STPT >SALT>ERT>LTPT，说明考虑优先因子(最高)和搬运时间(最短)的指派规则求解效果较好;②每组实验进行ANOVA分析得到的P-value值均接近于0，且明显小于0.05，这说明6种规则的求解效果存在显著差异;③在3000×5规模问题上，PRD均值的最小值由规则SANT取得，除此之外，PRD均值的最小值均由规则HP取得，并且规则HP的PRD均值和标准差的平均值均为最低，说明规则HP的求解质量最高，且性能稳定。

表1 6种单一规则的PRD均值、标准差与ANOVA分析结果

为了验证本文设计的组合规则的求解质量，对单一规则中求解效果较好的HP、SANT和STPT相互组合，形成6种组合规则并展开数据实验，实验结果如表2所示，最后两列为每组实验的F和P值。

根据表2可得：①6种组合规则的求解效果排序为SANT+HP>STPT+HP>HP(STPT)> HP(SANT)>SANT(HP)>STPT(HP)，说明由求解效果较好的单一规则所组成的求和规则比分层规则取得的求解效果更好；②每组实验进行ANOVA分析得到的P-value值均接近于0，且明显小于0.05，这也说明6种组合规则的求解效果存在显著差异；③PRD均值的最小值均由规则SANT+HP取得，并且规则SANT+HP的PRD均值和标准差的平均值均为最低，说明规则SANT+HP的求解效果最高，且求解性能最稳定；④在分层规则中，规则HP作为外层规则较SANT或STPT作为外层规则的求解效果好，这是由于分层规则首先以外层规则进行决策，而规则HP的求解效果优于规则SANT和STPT，因此对不同规则进行组合产生分层规则时，应优先把求解效果较好的单一规则作为外层规则。

表2 6种组合规则的PRD均值、标准差与ANOVA分析结果

为了验证表2中6种组合规则与表1中6种单一规则以及其他10种指派规则(HP(ERT)、ERT(HP)、ERT(STPT)、ERT(SANT)、STPT(ERT)、SANT(ERT)、STPT+ERT、SANT+ERT、HP+ERT和用来对比的随机选择规则RAND)的求解效果差异，图4给出了12组实验共120组算例中各指派规则取得TOP3调度解(同一算例取得的目标函数值可进入前三)和最差解的频次统计图。

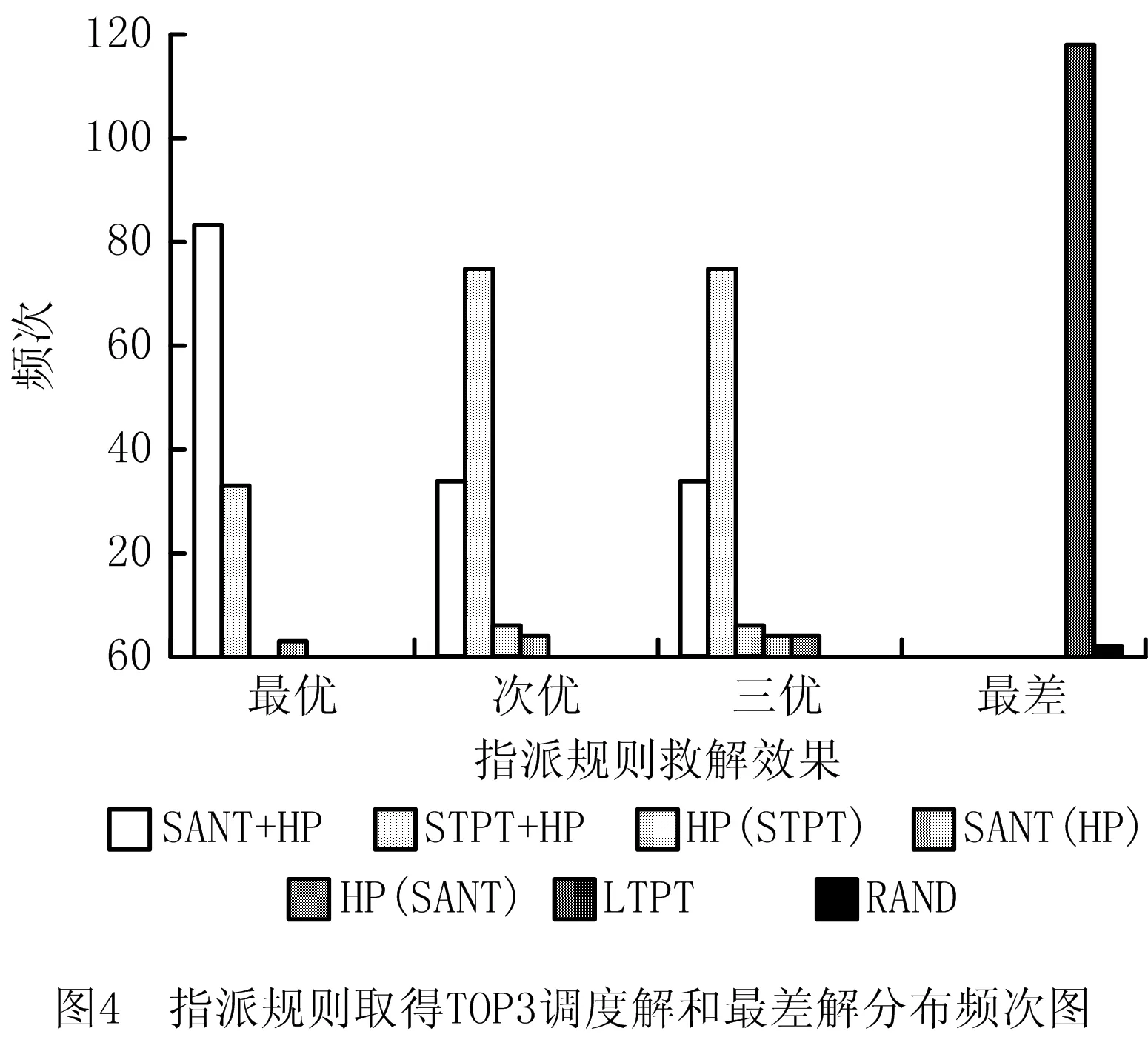
由图4可知，规则SANT+HP取得最优解83次，占比69.2%，取得TOP3调度解119次，占比99.2%，明显优于其他规则。其次是规则STPT+HP，取得最优解33次，占比27.5%，取得TOP3调度解118次，占比98.3%。规则LTPT的求解效率最差，共取得118次最差解，占比98.3%。

3.3 MAOCSA算法有效性实验

为了验证本文提出的MAOCSA算法的有效性。设置以下4个对比算法：①文献[17]提出的动态加权地图下改进的A*算法(Improved A*Algorithm under Dynamic Weighted Map，IA*DWM)；②文献[18]提出的层次规划算法(Hierarchical Planning Algorithm，HPA)；③算法MAOCSA-I：运用文献[17]中提出的路径规划算法解决多AGV路径规划问题；④算法MAOCSA-D：运用传统A*算法为每个AGV规划搬运路径，AGV在搬运过程中只能按此路径行走，不考虑搬运路径的动态更新。基于3.2节的实验结果，MAOCSA-I和MAOCSA-D均采用SANT+HP指派规则，用来验证MAOCSA算法中基于栅格阻塞度的路径规划算法的有效性，算法IA*DWM、HPA和MAOCSA-I均采用原文中推荐的算法参数。

实验参数设置如下：包裹数n=500，1 000，2 000，AGV数m=10，30，50，70，根据问题规模设计12组实验，每组随机生成10个算例，算例参数与3.1节相同，采用PRD(3.2节式(25))来衡量5种算法求解质量，并运用ANOVA对每组实验进行PRD均值差异性的显著性检验，假设α=0.05，对应的F临界值为2.58。表3的最后两列给出了每组实验的F和P值。

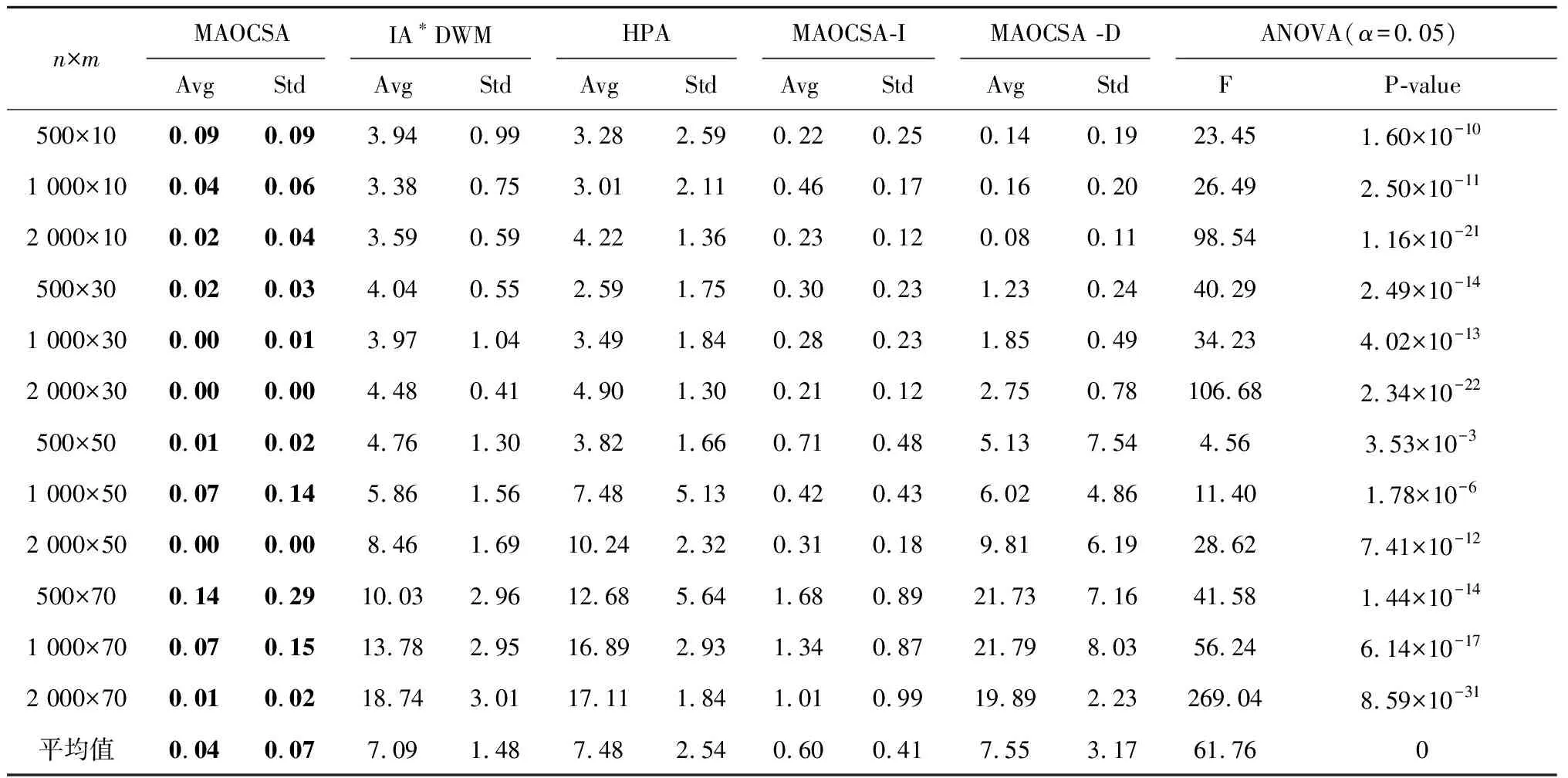
表3 5种算法的PRD均值、标准差与ANOVA分析结果

根据表3可得：①PRD均值的最小值均由算法MAOCSA取得，并且算法MAOCSA的PRD均值和标准差的平均值均为最低，说明MAOCSA的寻优能力最强，且求解性能最稳定。每组实验进行ANOVA分析得到的P-value值均接近于0，且明显小于0.05，这也说明5种算法的求解质量存在显著差异。②IA*DWM和HPA的PRD均值的平均值分别为7.09%和7.48%，明显高于MAOCSA(0.04%)，说明本文提出的MAOCSA算法的求解效果要明显优于IA*DWM和HPA，这是由于本文对任务指派与路径规划进行了协同优化。③MAOCSA-I的PRD均值的平均值为0.60%，高于MAOCSA(0.04%)，这说明本文提出的路径规划算法优于文献[17]的路径规划算法，这是由于本文根据问题特征设计了5种冲突AGV优先级规则，并且在栅格阻塞度的计算公式中考虑了AGV的拥堵时间，因此在解决多AGV间冲突和拥堵问题的基础上还能提高搬运效率。④MAOCSA-D的PRD均值的平均值最高(7.55%)，是5种算法中求解质量最差的，这是由于其他3种算法中每个AGV都可以根据自身获得的实时信息对搬运路径进行更新，而算法MAOCSA-D中每个AGV的搬运路径都是固定的，面对大量的冲突和拥堵，AGV将耗费较多的等待时间，这说明了对AGV进行在线实时调度的策略是有效的，也说明了本文提出的基于栅格阻塞度的路径规划算法的求解效果优于传统的A*算法。

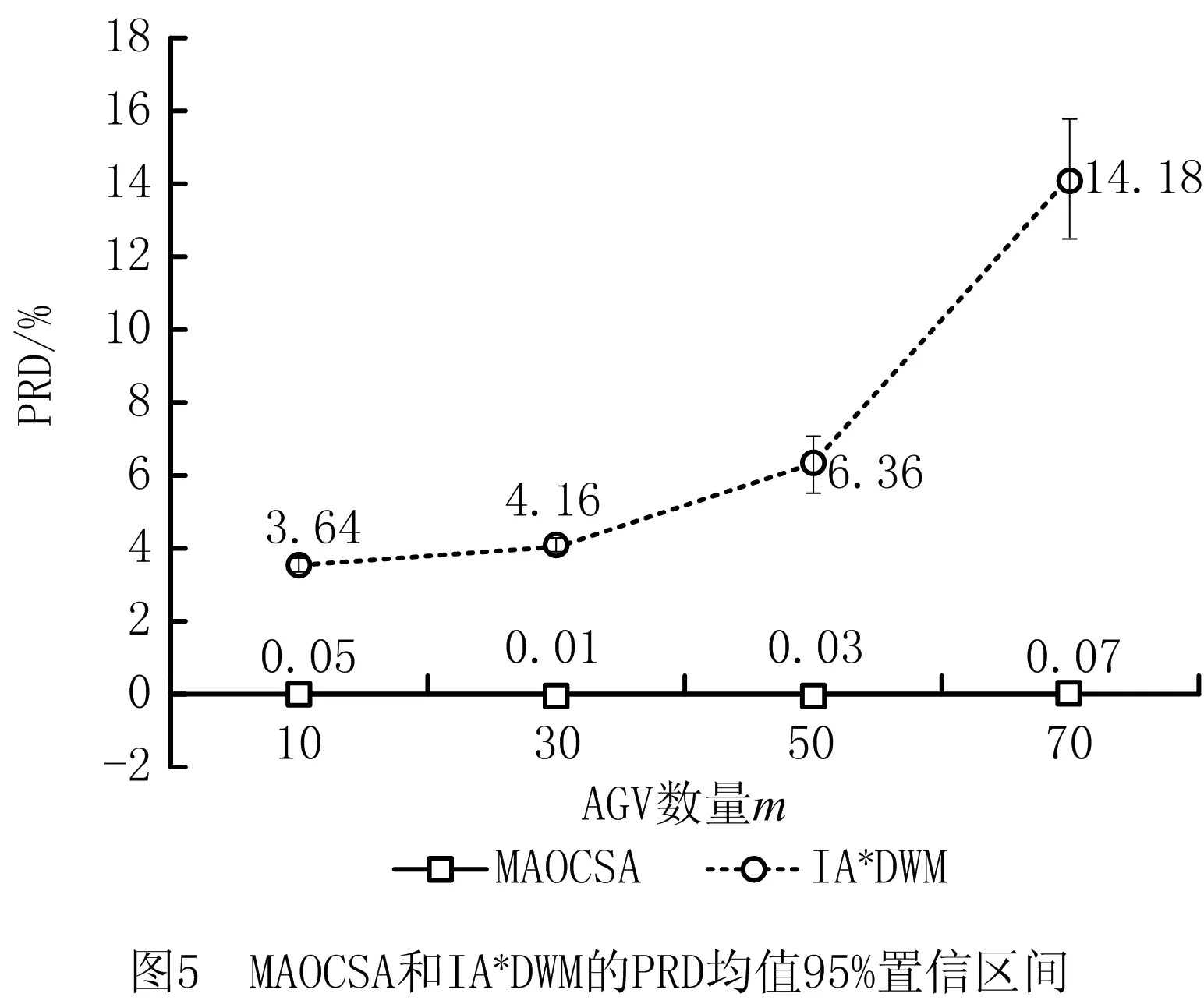
为了更好地观察AGV数量对算法求解效果的影响，根据表3的结果进一步汇总了不同AGV数量下算法MAOCSA和其他4种算法的PRD均值，并对其进行95%的置信区间分析，结果如图5～图8所示。

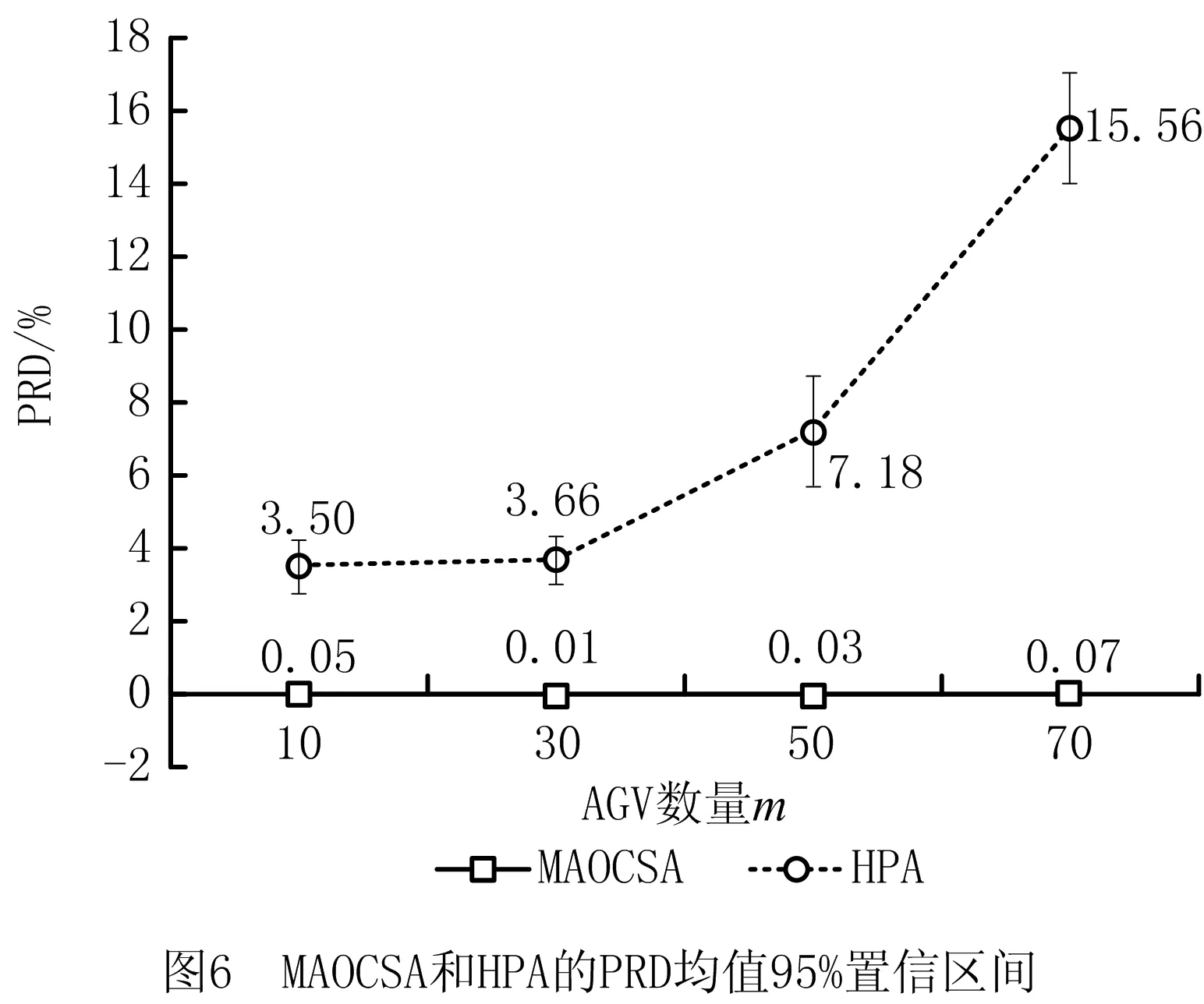
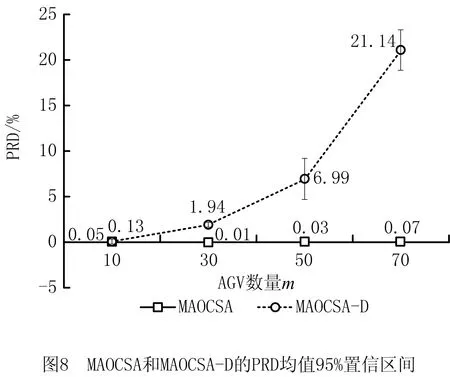
由图5～图8可知：①在不同的AGV数量下，MAOCSA的PRD均值始终低于其他4种算法，这说明MAOCSA在不同AGV数量下均能得到较好的解，且完全优于其他4种算法；②不同AGV数量下MAOCSA置信区间的区间长度也明显小于其他4种算法，表明MAOCSA解的分布比较集中，进一步说明了MAOCSA不仅能得到较好的解，并且算法具有较好的稳定性；③随着AGV数量的增加，4种对比算法的PRD均值基本都呈逐渐增大的趋势，而MAOCSA的PRD均值都在0.07%以下，且波动较小，这说明，AGV数量的增加会显著提高问题的求解难度，但MAOCSA算法能始终保持较好的求解效果。

4 结束语

本文以电商和物流企业自动化分拣仓库的实际分拣过程为背景，在动态环境下同时考虑了多AGV任务指派和无冲突路径规划，研究了多AGV在线协同调度问题。针对此调度问题，以最小化加权总搬运完成时间为优化目标建立了混合整数线性规划模型，并结合问题特征提出了一种多AGV在线协同调度算法。该算法通过集中决策方式对自动化分拣仓库及到达包裹的全局信息进行集中管理和调配，根据AGV的需要为其提供实时、准确的全局信息，并将每个AGV视为具有自主决策能力的Agent，各AGV自主调用指派算法和路径规划算法来确定搬运任务和行走路径。为支持AGV决策，设计了基于优先规则的指派算法和基于栅格阻塞度的路径规划算法。其中基于优先规则的指派算法是一个通用算法，算法可以调用包括随机指派在内的任意指派规则，指派规则一旦选定，算法将执行此规则生成指派方案，并进入路径规划进行协同优化，实现在线协同调度。进一步结合问题特征设计了若干具体规则，并通过实验分析确定了一种与本文问题适应性最高的指派规则；基于栅格阻塞度的路径规划算法通过预约表和冲突AGV优先级确定规则实现了无冲突路径规划，并且定义了栅格阻塞度来衡量仓库实时交通拥堵情况，各AGV在运行过程中会根据当前时刻的交通拥堵情况对搬运路径进行动态更新，以此来减少AGV对拥堵路段的过度占用和等待。最后，基于大量随机生成的算例展开仿真实验，实验结果表明，对于各种问题规模的随机算例，本文算法均具有良好的求解质量，且本文算法的求解性能稳定，具有良好的扩展性。

下一步将基于本文成果，进一步研究不同情况下各种决策规则的设计方式以及各自的适用性和有效性，设计更为高效的包含不同决策规则的指派算法，并运用神经网络等算法对决策规则进行在线学习，加强对算法适用场景的研究，并将设计的指派算法与路径规划算法进行集成，进一步提高在线调度效果。