美英早期解析几何教科书中的抛物线定义与方程
2022-12-04钱秦
钱 秦
(华东师范大学教师教育学院 200062)
1 引言
在数学新课程理念的倡导下,我国的数学教育正不断地进行数学文化和数学史融入数学教育的探索和实践,也取得了一定的成效.目前,在圆锥曲线一章,HPM视角下椭圆的课例最为丰富,也有不少学者进行了双曲线的尝试.但融入数学史的抛物线的课例屈指可数,笔者在知网上仅搜索到了4篇:文[1]从数学史中寻找启示,利用光学性质自然揭示抛物线的焦点、准线并建构解析定义,使学生厘清抛物线的来龙去脉;文[2]通过重构数学史的方式来设计教学环节,帮助学生突破焦点-准线定义及其由来;文[3]分析了圆锥曲线的历史,再采用重构式给出HPM视角下的椭圆、双曲线、抛物线及其标准方程的教学设计;文[4]采用发生教学法,从数学史、知识逻辑、学生的认知需求和生活实际出发,让学生在自主探索中将知识“再创造”出来,使抛物线知识自然发生.但这些课例所用到的历史素材十分有限.
国内现行高中数学教科书大多采用抛物线的第二定义(焦点-准线定义),且人教A版、沪教版、苏教版和北师大版教科书均在第二定义的基础上,以顶点为原点建立平面直角坐标系推导抛物线方程.在阅读材料中,沪教版教科书探究了二次函数的图象为什么是抛物线,人教A版和苏教版介绍了抛物线的光学性质,北师大版教材则呈现了圆锥曲线的截线定义.四个版本的教科书中关于抛物线的数学史元素都较少.
巧妇难为无米之炊,史料的匮乏是阻挡HPM视角下课例开发的最大障碍.早期教科书既体现了特定历史时期的教育理论或理念,也蕴含着编写者的智慧,为今日教学提供了丰富的素材和思想启迪.鉴于此,本文从有关数据库选取1820—1959年间出版的95种美英早期解析几何教科书(75种出版于美国,21种出版于英国,其中1种同时在两国出版),对其中抛物线的引入、定义与方程进行考察,试图回答以下问题:关于抛物线,美英早期解析几何教科书给出了哪些定义?采用了哪些推导方程的方法?以此思考抛物线的历史对今日教学的启示.
2 抛物线概念的引入
在这95种教科书中,有55种直接给出了抛物线的定义.其余40种则采用不同方法来引入抛物线的概念.
2.1 一般圆锥曲线定义
23种教科书先介绍圆锥曲线的第二定义或截线定义,再引入抛物线:根据点的运动规律可以产生无数轨迹,其中有一类尤为重要,这些曲线上的点到定点的距离与点到定直线的距离之比始终为常数,该曲线被称为圆锥曲线.[5]
2.2 二次方程
有6种教科书从一般的二元二次方程引入:Ax2+Bxy+Cy2+Dx+Ey+F=0为一般的二元二次方程,其中A,B,C,D,E,F均为常数,这个方程所代表曲线的性质会随着系数的特定值变化而变化……若B2-4AC>0,方程代表两条双曲线;若B2-4AC<0,方程代表一条抛物线;若B2-4AC=0,方程代表一个椭圆.[6]
2.3 轨迹问题
有3种教科书从轨迹方程问题引入.考虑下面的轨迹问题:一个动点到一条固定直线和一个固定点的距离相等,试确定动点轨迹的性质.[7]
2.4 二次函数
有3种教科书通过一元二次函数引入.形如ax2+bx+c,a≠0的表达式称为x的二次函数,曲线y=ax2+bx+c的纵坐标表示一条抛物线的函数.[8]
2.5 圆锥曲线的历史
有5种教科书通过圆锥曲线的历史引入,如Roberts和Colpitts在书中写道[9]:
椭圆、双曲线和抛物线统称为圆锥曲线,这一名称源于这样一个事实,这些曲线都可以由一个平面截圆锥得到.这些曲线的许多性质为希腊早期几何学家所知,其中主要的研究者是阿基米德和阿波罗尼奥斯.阿基米德计算了抛物弓型和椭圆的面积,阿波罗尼奥斯发现三条曲线都可以从同一个圆锥上截得,并研究了许多双曲线的特殊问题.许多世纪以后人们才发现圆锥曲线的知识在研究宇宙规律方面有很大的实用价值.大约1600年,德国的开普勒发现了它们在天体运动研究中的重要性,与此同时,意大利的伽利略发现炮弹的轨迹是抛物线.直到人们意识到物理学、力学和建筑领域的大量问题都依赖于圆锥曲线的知识来解决,它们的应用领域才得到扩展.
3 抛物线的定义与作图
3.1 抛物线的定义
在所考察的95种教科书中共出现了4种抛物线的定义.
第一种是古希腊的截线定义,26种教科书给出了截线定义:平面斜截一圆锥面,当截面平行于一条圆锥面的母线(但不过圆锥顶点时),平面与圆锥的交线称为抛物线.[10]
第二种是第二定义,86种教科书给出了第二定义:抛物线是一条平面曲线,其上的点到定点与到定直线的距离相等.定点为抛物线的焦点,定直线为准线.[11]
第三种是极限定义,将抛物线视作椭圆或双曲线的极限,有6种教科书采用了极限定义:给定椭圆的一对顶点和焦点,假设它的长轴无限增大,则该曲线最终会成为抛物线.[6]
第四种是特殊的比例定义,只在所考察的3种教科书中发现.抛物线是一些点的轨迹,这些点到两条垂直直线的距离满足这样的关系:点到一条直线距离的平方与点到另外一条直线的距离成正比.[12]
95种美英早期解析几何教科书中所采用抛物线定义如图1所示.可以发现在4种定义中,第二定义和今天一样受人们青睐,出现的频率最高.而历史悠久的截线定义也受到了不少教科书的关注,这与今天截然不同.也有一些教科书给出了抛物线的多种定义,即将截线定义、极限定义和比例定义作为第二定义的补充定义出现,但是20世纪20年代后的教科书已经舍弃了比例定义和极限定义.

图1 95种早期解析几何教科书中的抛物线定义
3.2 抛物线的作图
早期的解析几何教科书也十分注重抛物线的作图,共出现3种作图法.
第一种作法:利用三角尺和绳子构造抛物线.先作抛物线的准线和对称轴,如图2,在准线处放置一把直尺,将Rt△EDG的一条直角边ED贴紧直尺,并将一条与DG边等长的绳子一端固定在G处,绳子另一端固定在对称轴上的点F处.当直角三角形沿着准线上下移动时,放置铅笔P使得绳子始终保持紧绷,那么铅笔会画出抛物线的一部分.当然,这只能画出抛物线的一部分,因为抛物线可以无限延伸[11].

图2 三角尺构造抛物线 图3 平行线构造抛物线
第二种作法:平行线和同心圆相交法.如图3,记DD′为抛物线的准线,F为抛物线的焦点.过点F作DD′的垂线GG′,然后过F作HH′垂直于GG′,使得FH=FH′=FG,易知H和H′是该抛物线上的两点.连结GH和GH′并延长,构造一系列平行于HH′的直线分别交GH和GH′于点a,b,c,d,…和点a′,b′,c′,d′,….以点F为圆心、dd′为直径作圆,交dd′于点P和P′,这两点即为抛物线上的点.采用类似的方法,我们可以找到抛物线与aa′,bb′,cc′,…的交点.用一条平滑的曲线连接所有这些点,就得到了抛物线.[13]
第三种作法:利用抛物线的内在性质作图.抛物线具有这样的内在性质:抛物线上每一点到对称轴的距离的平方等于该点到顶点的水平距离乘以2倍焦准距,这给我们提供了一种作抛物线图象的方法.如图4,已知抛物线的准线为l,焦点为F,易找到抛物线的顶点V.在抛物线的对称轴上任意地选取一点M,我们可以算出VF和4VM的等比中项,过点M以该等比中项的长度作对称轴的垂线MP,P是以l为准线、F为焦点的抛物线上的一点.同理,通过选取对称轴上不同的点,我们就可以得到该抛物线上的许多点.[14]

图4 利用内在性质 构造抛物线
4 抛物线方程的推导
95种教科书中,有8种或直接给出标准方程,或只研究了抛物线的几何性质而未给出标准方程,其余教科书均对标准方程进行了详细推导,共出现了4种定义下的推导方法.
4.1 基于截线定义的推导
有1种教科书利用旦德林单球模型联系抛物线的截线定义和第二定义.如图5,圆锥中有一球与圆锥内表面相切,M,T是切线上的两点,用平行于母线VB、外切球于F,且与平面VOB相垂直的平面截取圆锥面,则截线为抛物线.已知平面VOB⊥截面PDE,且平面VOB⊥平面DEM,所以平面VOB垂直于平面DEM和平面PDE的交线DE,那么DE垂直于平面VOB上的EE′.MN∥截面PDE,则MN平行于截面PDE和所有过MN平面的交线,那么MN∥PD∥EE′,所以PD⊥DE.一组平行平面所截的两条平行线相等,即PD=MN.易知MN=PT,又因为切线PF=PT,所以PD=MN=PT=PF.因此,我们可以将抛物线定义为这样一条平面曲线,曲线上的点到一定点(F)与定直线(DE)的距离相等.[15]根据这个事实,我们可以用解析几何的方法推出抛物线方程.

图5 旦德林单球模型

4.2 基于第二定义的推导
有19种教科书以准线为y轴建立直角坐标系进行推导.如图6,以准线YY′为y轴,然后过焦点作准线的垂线(即抛物线的对称轴),并将其作为x轴建立平面直角坐标系,令OF=2p.根据抛物线性质知PF=PN=OM,所以PF2=OM2,得FM2+PM2=OM2,即(x-2p)2+y2=x2,故得y2=4p(x-p).令y=0,我们得到x=p,即抛物线与x轴交于点A(p,0),若以A为原点,则x=x′+p,于是得新方程y2=4px′.[17]

图6 以准线为y轴 图7 以顶点为原点


图8 从极坐标进行推导
4.3 基于极限定义的推导
有4种教科书采用抛物线的极限定义推导其标准方程.

图9 基于极限定义推导2
4.4 基于比例定义的推导

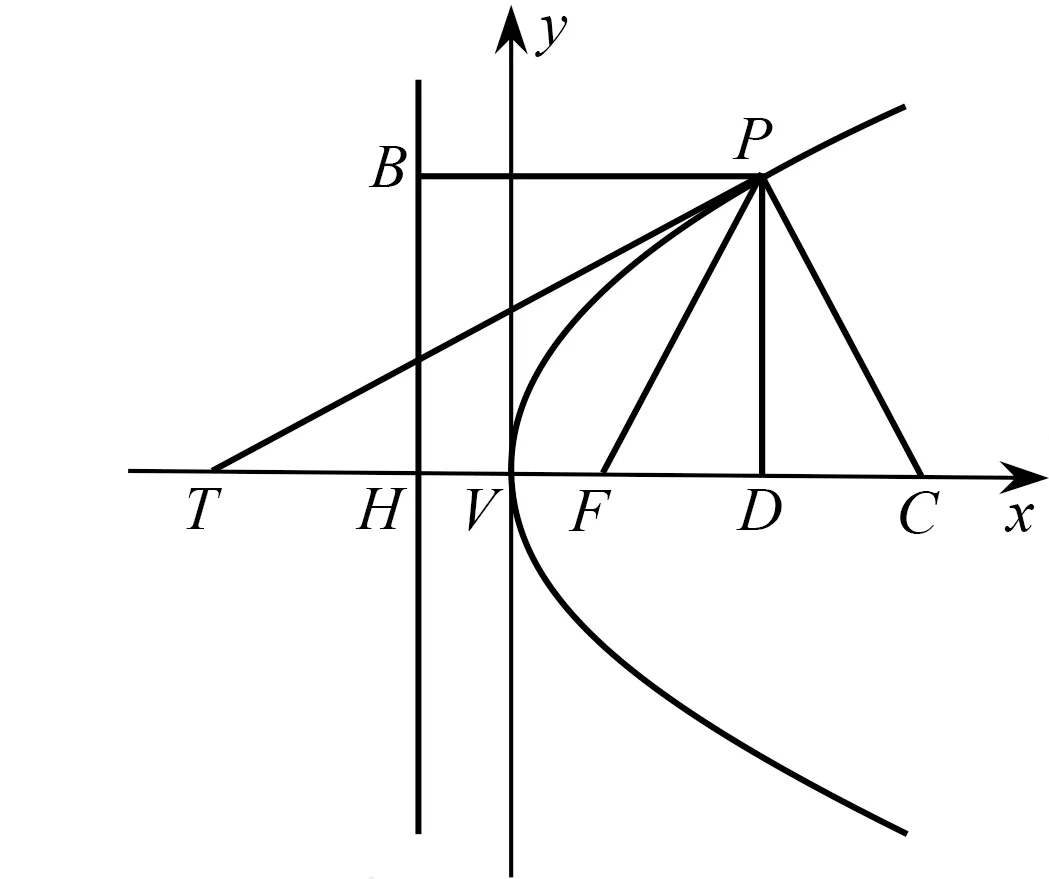
图10 基于比例定义的推导
5 结语
由上可见,美英早期解析几何教科书中抛物线的定义和方程推导方法均呈现多样化的特点.早期教科书中给出了抛物线的4种定义,并且从4种定义出发分别推导了抛物线的标准方程,在推导过程中综合运用了丰富的几何、代数及三角学的知识.然而,随着时间的推移,现代中学教科书中的抛物线定义与推导方法均趋向单一.早期教科书给我们带来如下启示:
其一,追本溯源,重视几何本质.众所周知,圆锥曲线是高中解析几何部分的重要内容,而解析几何的核心是用代数的方法来研究几何问题.通过建立平面直角坐标系,复杂的几何判断就可转化成代数运算,为几何的研究带来了便利.但正是在这种极度的便利下,人们往往将圆锥曲线视为解析几何概念.但从历史上看,圆锥曲线是一个几何概念,最早由古希腊的数学家梅奈克缪斯(Menaechmus)用垂直于母线的平面去截顶角为锐角、直角和钝角的圆锥所得到.后续人们对圆锥曲线作了不少的探索,但在创立解析几何这门学科以前,人们一直采用古希腊人的截线定义,将圆锥曲线放在立体几何中进行研究.因此,抛物线教学不能仅从解析几何的角度开展,也应从更广的立体角度对其进行探究.截线定义是抛物线的来源,理应为学生所知晓,而极限等补充定义则由教师根据需要选择是否讲授.
其二,各取所长,展现方法之美.现代教科书中关于抛物线方程的推导虽然简洁,但过于单一且理想化.学生一定能想到以顶点为原点吗?学生没有其他想法了吗?仅讲解书上的一种方法是不够的,单一的方法限制了学生思维的发展.教师可以放手先让学生探究,再根据学生的思路适当作些补充.例如,准线是抛物线定义中天然存在的一条线,学生用准线作为y轴相当自然,这也是早期教科书中使用频率相当高的一种方法.教师还可以选择性地讲解历史上的其他推导方法,让学生体会不同方法背后的思想之美.
其三,注重联系,构建知识之谐.一方面,学生在初中时期就已经对一元二次函数y=ax2+bx+c(a≠0)的图象为抛物线了然于心.如何让学生理解二次函数图象与当今课堂学习的抛物线同质是教学的一大重点,这里主要涉及坐标的平移变换.另一方面,如果向学生介绍圆锥曲线的来源,也应说明截线定义和第二定义的等价性.旦德林单球模型是沟通截线定义与第二定义的良好桥梁,但使用的难度较大.教师应根据学情,通过搭建脚手架,构造实物模型等方式来降低教学难度.
