回归·拓广·升华——以一道解三角形试题的分析历程为例*

王 耀

(江苏省苏州第一中学 215006)

笔者在近期的高三一轮复习中，发现一道解三角形选择题的准确率不高，于是以此为契机，精心构思，通过师生合作将一些相关知识点完美串联起来，具体讲评历程整理如下.

1 问题呈现

2 知识梳理

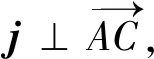
教材溯源1(人教版教材第54页“综合运用”第17题)证明：设△ABC的外接圆的半径是R，则a=2RsinA，b=2RsinB，c=2RsinC．

简证(1)当△ABC是锐角三角形时，外接圆O半径为R，如图1，连结BO并延长，交外接圆于点A1，连结A1C，则圆周角∠A1=∠A.

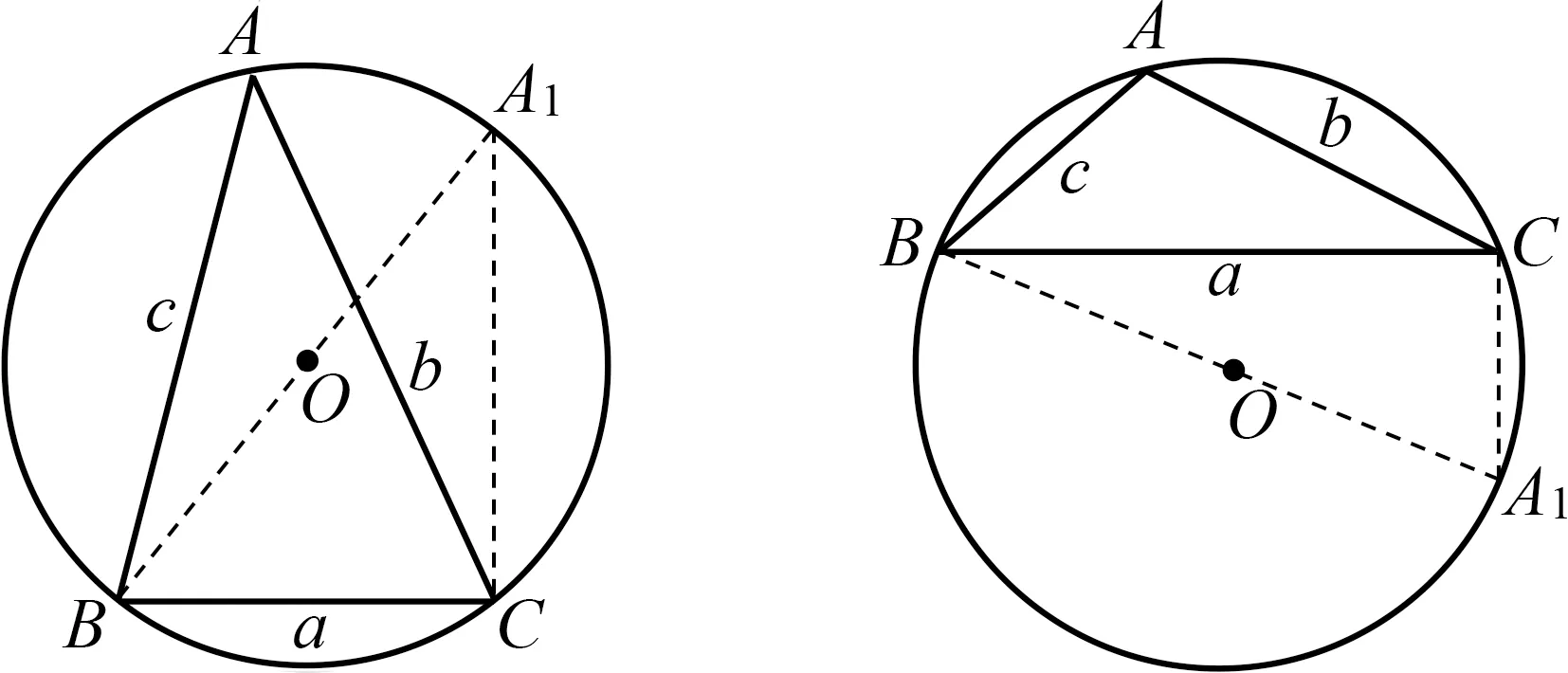
图1 图2

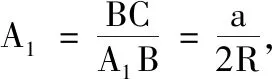
3 问题解决

在批阅这道题时，笔者发现得分率相对较低，询问后得知即使答对的学生，也有部分是通过对三角形特殊化后“猜对”的答案．因此，在讲解前，笔者特地回顾教材，对正弦定理的来龙去脉进行回顾(知识梳理部分)．这样处理后，许多学生再面对这道题时，得到以下解法：

图3

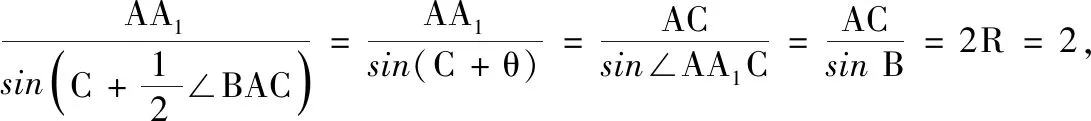
解法1中，通过初等几何知识(圆周角相等)以及正弦定理的拓广结论进行求解，让解题思维不只是“冰冷的美丽”，能否继续展开“火热的思考”，也是值得探究的问题．除了采用“化角”的转化策略，笔者也尝试进行“化边”转化，进而引导学生进行思考，将解法2的教学片段整理如下.

师：在解三角形中，由三角形的角平分线能想到什么性质或结论？

图4

生2：相交弦定理，也就是利用△A1BD∽△CAD可知BD·DC=AD·DA1.

师：生2讲得很全面，问题转化为求出角平分线AD的长度，怎么求解呢？

师：上面对三角形中内角平分线的定性分析、定量计算，复习了经典的结论，现在请大家将上面的信息综合起来，推导一下线段AA1的长度表达式.

评注(1)这个解法中，综合运用了多个定理，如角平分线定理、相交弦定理、余弦定理、角平分线长公式等，其中，与角平分线相关的公式、定理都是命题中的热点，本文下面会举例说明．

图5

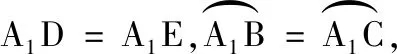
多么简洁的方法，的确让大家眼前一亮，笔者和学生一起感受这道题蕴涵的数学之美，也有学生提出能不能利用余弦定理来证明这个结论？结合前面的解法，师生讨论后发现这个方向是可行的．

解法4如图6，设∠BAC=A=2θ，则∠BAA1=∠CAA1=∠BCA1=∠CBA1=θ，可设A1B=A1C=x．

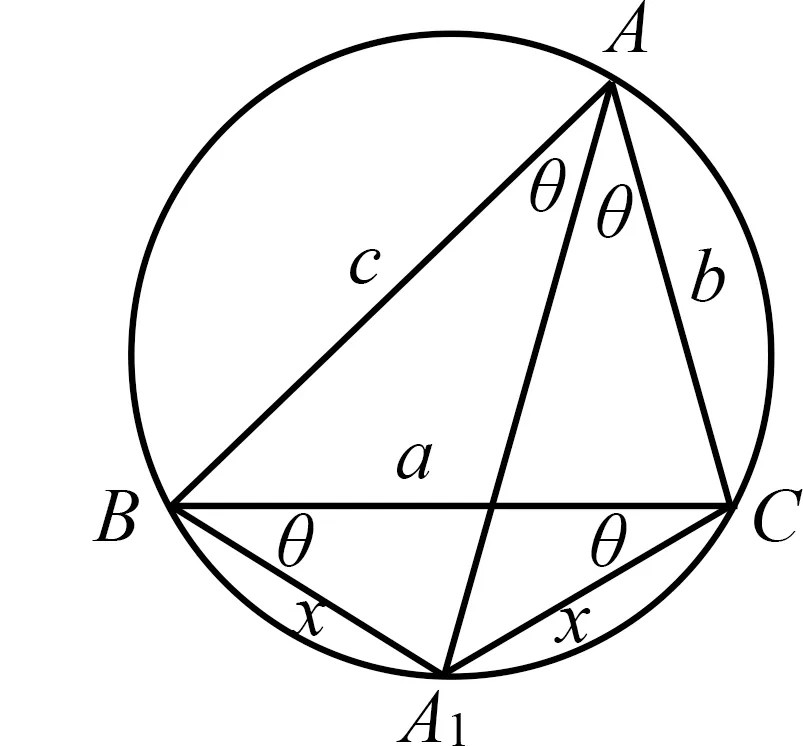
图6

真是条条大路通罗马啊，一道小题竟然可以有几种方法去研究它，不知不觉地就过了一节课．课后，笔者也意犹未尽，继续思考，得到如下更为简洁的解法：

4 拓展运用

为了巩固上文中的一些解题策略，笔者选取了几道习题供学生进行练习，升华思维．

图7

例1(2018·江苏卷13)在△ABC中，角A，B，C所对应的边分别为a，b，c，∠ABC=120°，∠ABC的平分线交AC于点D，且BD=1，则4a+c的最小值为．

图8

评注此题也可以运用几何法进行直观想象，即利用角平分线定理构造调和点列，得到结果，但是用解析法进行逻辑推理更加严谨，可培养学生数学推理、数学运算的能力．

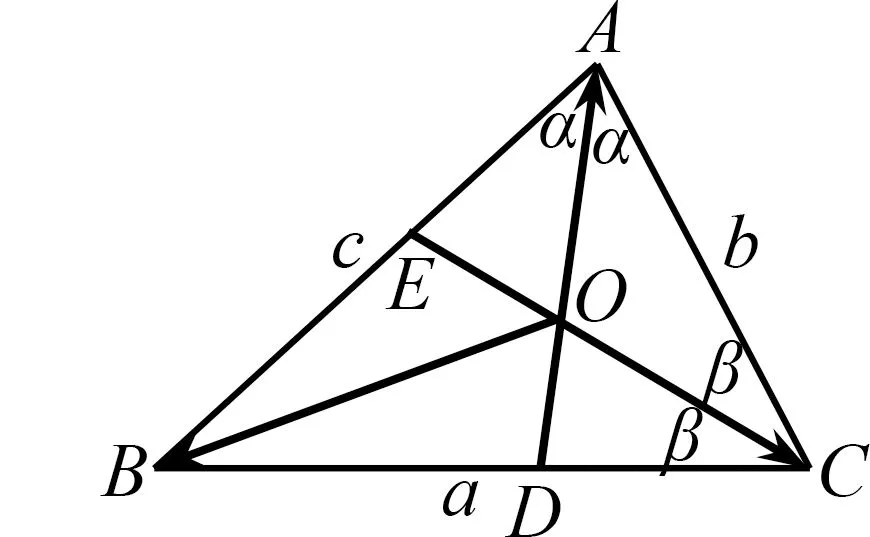
图9

评注在人教版新教材第64页中，让学生用向量法研究三角形的性质进行数学探究的研究活动，本例恰好是在所学知识基础上，对三角形的内心进行向量表示的完美体现．

例4(2021·全国I卷19)记△ABC的内角A，B，C的对边分别为a，b，c．已知b2=ac，点D在边AC上，BDsin∠ABC=asinC．

(1)证明：BD=b；(2)若AD=2DC，求cos∠ABC．

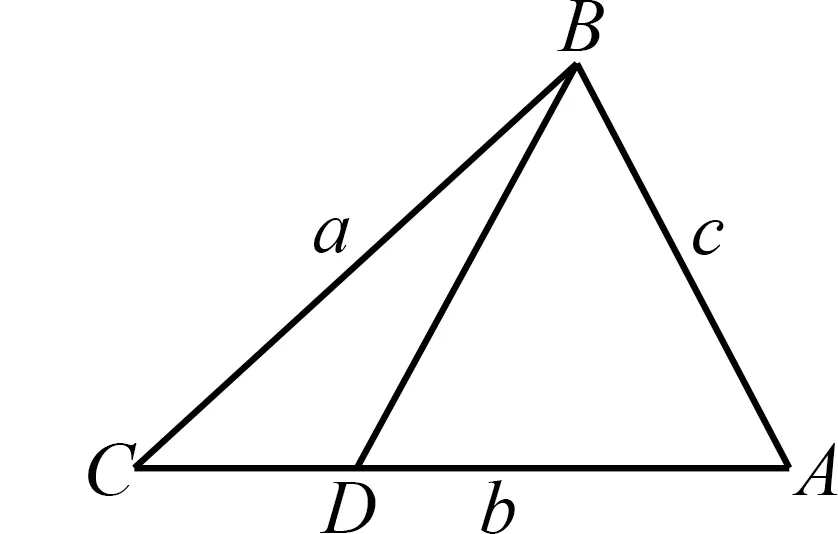
图10

评注这道题虽是中档题，但是从学生反馈来看，不少人用时较多．可见，将未知的问题转化为熟悉的结构特征，选择有效的转化策略尤为重要，本题由定比分点进行向量表示是最高效的解题途径．

5 教学感悟

(1)回归教材，理解数学

2017年版课程标准指出，通过高中数学课程的学习，获得进一步学习以及未来发展所必需的数学基础知识、基本技能、基本思想、基本活动经验(简称“四基”)；提高从数学角度发现和提出问题的能力、分析和解决问题的能力(简称“四能”)．高考命题的依据是“课标”“考纲”与“教材”，命题源于教材但又高于教材，这是全体高三教师的共识．那么，高三数学备考的课堂教学中，提升“四基”“四能”，离不开对教材的深刻理解．章建跃教授近年来倡导的“理解数学”[1]引起了广泛的关注，他提出，教好数学的前提是要理解数学，只有理解数学知识的本质，才能积累教学知识的表达经验．

的确，通过文中分析的这道题不难看出，对于广大师生而言，理解教材是教师教好数学、学生学好数学的关键，教材中的定理和一些典型的例习题之间常具有一定的关联性，其中渗透了某些经典的数学思想方法．因此，在高三的复习工作中，要认真研读教材，充分发掘教材的使用价值，通过对教材的深入思考与研究，帮助学生系统地梳理知识，构建知识网络．例如，本文中通过对正弦定理背景下的习题讲评的设计，师生共同探究问题的背景、方法和联系，帮助学生积累问题解决过程中常用的解题经验．

(2)拓展探究，建构数学

教学的目的是使学生学会未知的知识，逐步由“学会”到“会学”．也就是说，学生在学习过程中接受新知识，更重要的是要学会如何独立思考．因此，笔者认为给学生提供合适的研究对象，进行拓展研究，显得尤为必要．这些素材广泛分布在教材中，例如正文、思考、旁白、例习题等．

在高考复习教学中，如果只是对知识点重复罗列，无法提高学生学习的参与度和内驱力．不妨注重联系，“合纵连横”地进行知识体系的再建构，即通过“点—线—面”的方式，将教材中的关联知识点灵活呈现[2]，在教师的引领下，学生对概念、定理、公式的来龙去脉进行再认识，对教材知识进行再巩固，提高知识综合运用的能力，提升问题解决的成功率．

本节课中研究的问题，与三角函数、向量、正弦定理、余弦定理、不等式、初等几何等知识之间有着密切的联系，这些知识都是解决几何问题的有力工具．通过对其中分析思维历程的展示，让学生领会到知识的精髓，积累数学探究的活动体验．

(3)强化运用，升华思维

以“微点”入手的课堂教学是近年来高三数学复习中的常见课型[3]，教师精心选择素材，结合归类设计、变式开发等手段完善讲评策略，通过学生自主探究、师生合作探究，对知识进行运用和拓展，探究解法联系，还原问题本原，从而引导学生积极、主动地矫正思维问题，深入体会数学思想方法，拓宽思维的广度，发掘思维的深度，进一步完善知识结构．这样的课堂设计，常需要从微观和宏观两个层面进行构思，师生积极参与，使高三的数学课堂充满生机活力，对学生思维的发展、创新精神的培养和实践能力的提高有积极的作用，对教师课堂教学效率和品位的提高有参考价值．

通过本节课中的问题解决过程发现，解法之间有联系，更有创新，各具特色，解题过程不再是“冰冷的形式化美丽”，而是那种发散的、火热的思考过程，达到了数学思维的自然流淌．由此可见，面对数学问题，只要我们学会广泛的联想和生动的类比，我们就会拥有宽阔的思路，探究出各式各样的方法.如果在解题过程中，对于每一个细节再进一步深入思考，继续追寻下去，那么解法还能不断改进，不断优化，化复杂为简单，聚分散为统一．这一切不仅可以提高我们发现问题、解决问题的能力，更是一种数学美的享受．

总之，提高学生的问题解决能力和提升学生的数学思维品质，是数学解题教学的永恒主题．作为教者，应善于引导学生重视知识背后的结构、联系和规律，积累问题解决过程中的思维经验，追求知识能力的应用和迁移，从而让教师的课堂教学更加精彩，最大限度地促进学生数学素养的有效落实．