平行线中的“截线”

内蒙古师范大学数学科学学院　徐俊文

平行线中的“截线”

内蒙古师范大学数学科学学院徐俊文

《平行线的性质与判定》是初中几何教学的开始，教学中由于简述判定定理与性质定理，极易使学生产生没有“截线”或“截线”可有可无的误区，事实上，“截线”在平行线的判定定理与性质定理的使用中起着至关重要的作用，本文结合教学实践阐述了“截线”在平行线的性质与判定定理的使用中的重要作用以及使用方法，教学中应更加注意强化学生对“截线”重要作用的认识.

平行线几何教学截线

平行线中的“截线”是平行线的性质定理和判定定理应用的基础，但在日常教学中，为了方便学生记忆定理，在叙述定理时，我们往往采用简述的方式，如“内错角相等，两直线平行”、“两直线平行，同位角相等”.这种简述的方式，往往会使学生忽视“截线”的存在，甚至认为“截线”不存在.事实上，定理的完整叙述中都提到了“截线”这一条重要的直线，如“如果两条平行直线被第三条直线所截，那么同位角相等”、“两直线被第三条直线所截，如果内错角相等，那么两直线平行”，如果“截线”不存在，那么“同位角”、“内错角”、“同旁内角”都将不存在，是不能应用性质定理及判定定理的.所以，在教学中适当的强化“截线”的存在是必要的，适当的总结拓展一些依靠“截线”而存在的角的求法和相关问题的解法不但会使学生加深对定理中“截线”的认识，更能让学生了解几何问题研究的方法，开拓学生学习几何的视野.下面结合平行线性质定理及判定定理中的几个例题，谈谈“截线”在平行线中的不可忽视的作用.

一、两直线被一条直线所截

1.性质定理的应用.

例1．已知：如图1，a∥b，∠1=56°，求其余各角的度数.

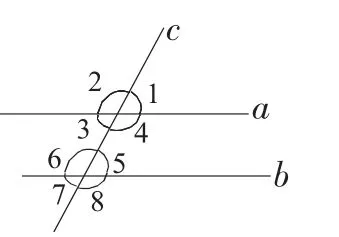
图1　

解：∵a∥b，∴∠5=∠1=56°，

∴∠7=∠5=56°，∠3=∠1=56°，

∵∠1+∠2=180°，

∴∠2=180°-∠1=180°-56°=124°，

∵a∥b，∴∠6=∠2=124°，

∴∠8=∠6=124°，∠4=∠2=124°.

评析：题目中，虽没有提到“截线”c，但正是因为有了“截线”才构成了这八个角，八个角当中不仅是已知了∠1的大小，可以求出其余各角，而是只要已知其中任何一个角，就可以求出其余各角.

2.判定定理的应用.

例2.已知：如图2，∠1=∠2，求证：a∥b.

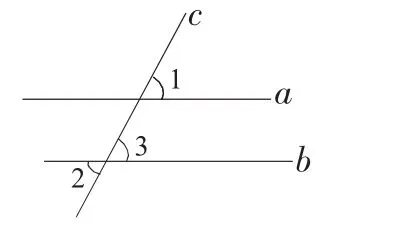
图2　

证明：∵∠2=∠3， ∠1=∠2，

∴∠1=∠3，∴a∥b.

例3． 如图3，已知∠1=120°，∠A=60°，判断直线AB与CD是否平行，并说明理由.

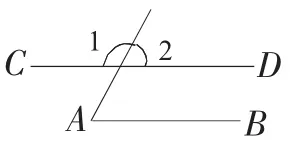
图3　

解：AB∥CD，理由如下：

∵∠1+∠2=180°，

∴∠2=180°-∠1 =180°-120° =60°，

∴∠A=∠2， ∴AB∥CD.

评析：以上两个题的题设部分均没有提到“截线”，但是为证明直线平行所需要的同位角都是依赖于“截线”存在的，因此在解决与“判定直线平行”有关的问题时，只要找准了“截线”，再结合需要证明的平行的直线，便很容易找到证明直线平行所需的同位角，内错角，同旁内角.

二、两直线被两直线所截

1.性质定理的应用.

例4.如图4，若已知∠1、∠2的大小，便可如例1所示求出其余的14个角的大小；若旋转直线d至与直线c平行，如图5，则只需知道其中一个角的大小，便可由例1所示的方法，求出其余15个角的大小.

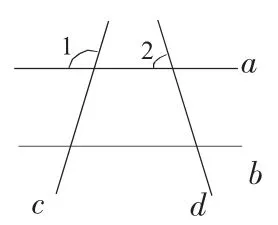
图4　

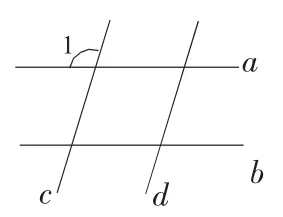
图5　

因此，能正确识别“截线”，并根据“截线”的位置正确使用“截线”及其相关的结论，可以化未知为已知，化难为易.

2.判定定理的应用.

例5.如图6，下列推理错误的是（）

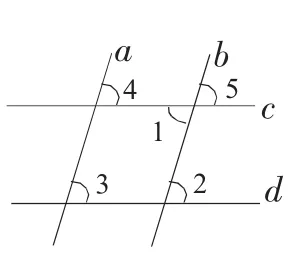
图6　

A.∵∠2=∠5，∴c∥d

B.∵∠3=∠4，∴c∥d

C.∵∠1=∠3， ∴c∥d

D.∵∠2=∠3，∴a∥b

答案：C

评析：此题中关键就是要分清判断直线平行的角是依赖哪条截线存在的，且应注意，两条直线平行与否应根据推理，不应根据视觉感觉.

三、两直线被三直线所截

性质定理与判定定理的综合应用的经典例题及其变式练习.

例6．如图7，已知，点A、B、C在同一条直线上，点D、E、F在同一条直线上，且∠A=∠F，∠C=∠D.求证：AE∥BF.

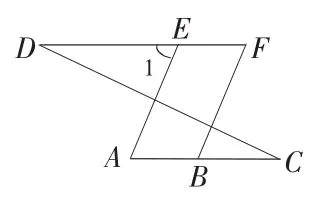
图7　

证明：∵∠C=∠D，

∴DF∥AC.∴∠A=∠1，

又∵∠A=∠F，

∴∠F=∠1，

∴AE∥BF.

变式.如图8，已知∠1=∠2，下列结论正确的是（）

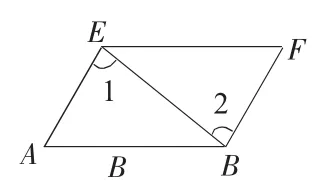
图8　

A.AB∥EFB.AB∥BF

C.AB∥EF，AE∥EF

答案：B

评析：此图就是将例6中的点C沿着BA方向滑动至与点B重合，点D沿着EF方向滑动至与点E重合，但仍然是两直线被三条直线所截的问题.

平行线中有了“截线”，才有了角，才能构成相等、互补的角，反之相等、互补的角才能判定直线平行，因此，“截线”在平行线中起着至关重要的作用，在教学中不可忽视.