单粒子辐射导致的VDMOS 体二极管反向I-V 曲线蠕变现象研究
2022-12-03吴玉舟李泽宏李陆坪任敏李肇基
吴玉舟,李泽宏,李陆坪,任敏,李肇基
(电子科技大学 电子薄膜与集成器件国家重点实验室,四川 成都 610054)
单个高能粒子入射到半导体材料中引起集成电路或器件逻辑错误、脉冲干扰、甚至设备烧毁的现象称为单粒子辐射效应。单粒子辐射效应最早发现于1975年,之后文献报道的单粒子辐射产生的现象越来越多,包括单粒子烧毁、单粒子栅穿、单粒子翻转、单粒子扰动、单粒子闭锁、单粒子瞬间脉冲等。VDMOS 器件中常出现的单粒子现象主要是单粒子烧毁(Single Event Burnout,SEB)和单粒子栅穿(Single Event Gate Rupture,SEGR)。SEB 现象在1986 年被首次报道[1],该现象主要发生在器件工作于阻断状态。SEGR 现象于1987 年被首次报道[2],该现象会发生在VDMOS 器件工作的各个状态,其中器件处于阻断状态时,SEGR发生的几率最高。SEB、SEGR 被称为是器件的硬错误,会对VDMOS 器件产生永久性损坏[3-5],因此在空间辐射环境中应用的半导体器件必须进行抗单粒子辐射加固,以防止器件损毁导致整个电子系统失效[6-13]。
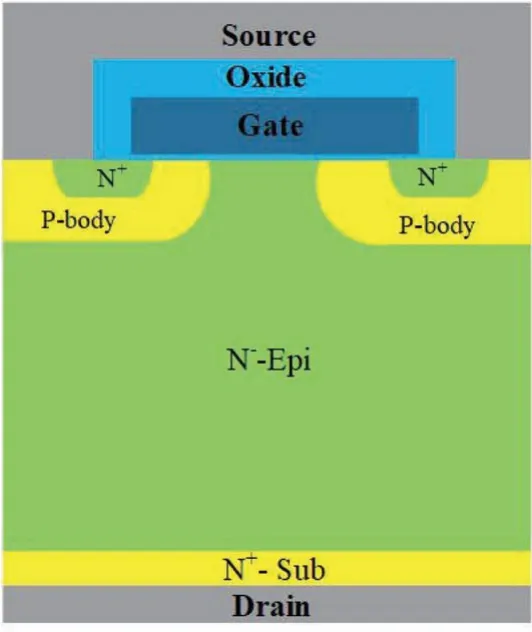
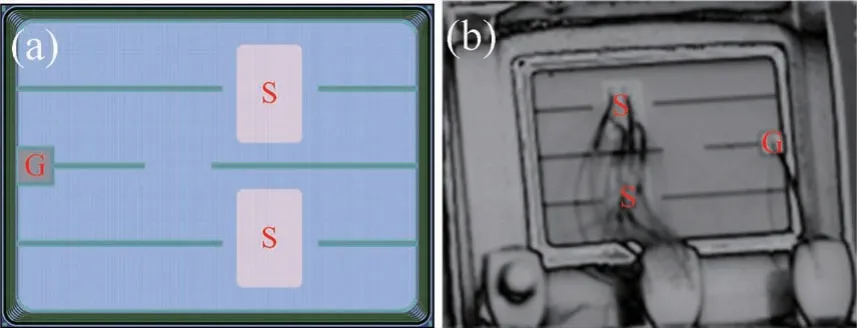
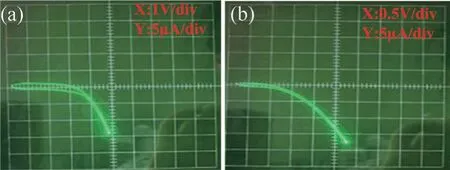
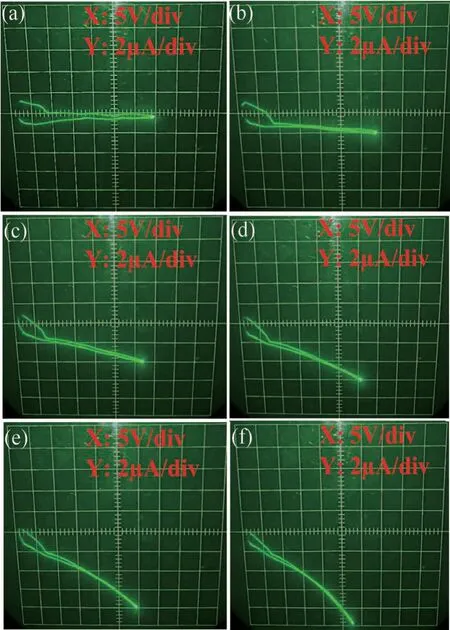
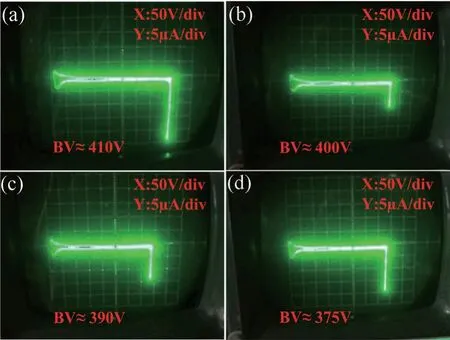
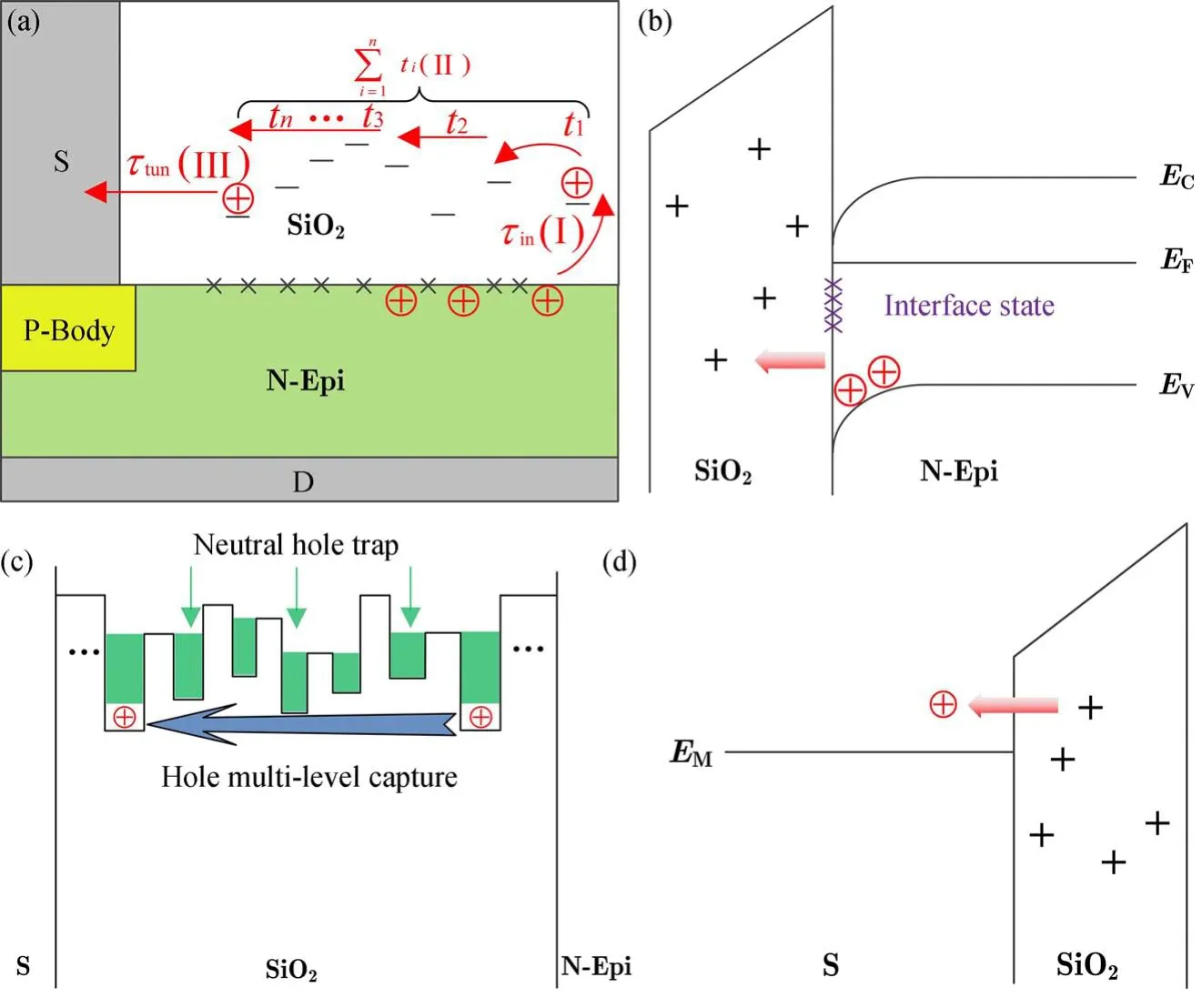
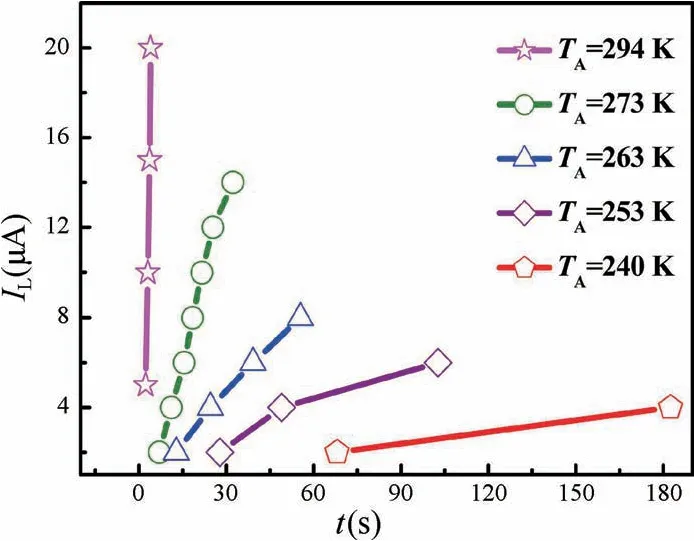
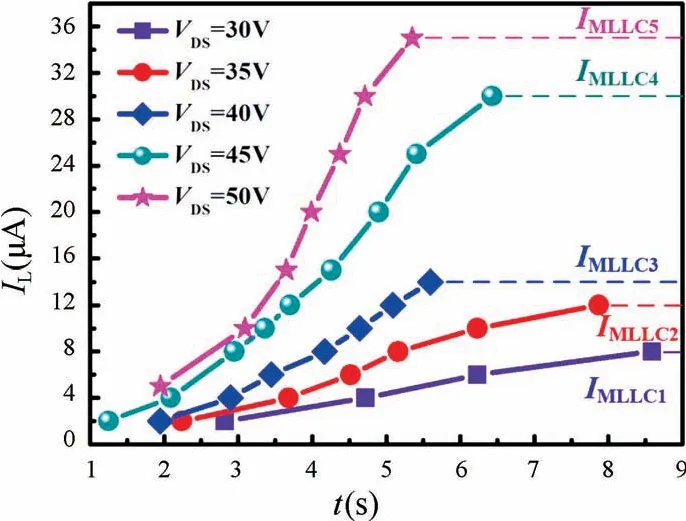
在单粒子辐射过程中,VDMOS 器件的栅结构会存在介于栅氧化层完整(Gate Oxide Integrity,GOI)和SEGR 之间的状态,即栅氧化层漏电流较大(几十微安至数百微安级),但并未被完全损坏,称之为软击穿状态[14-16]。原因在于氧化层中存在缺陷能级,载流子在电场作用下由Si-SiO2界面处通过缺陷能级跃迁至栅极形成漏电流。对于单粒子辐射下界面态缺陷的产生,有诸多文献对其进行实验说明,并提出了纳米点的概念[17-19]。单粒子辐射后,通过化学刻蚀去除表面SiO2,使用扫描探针显微镜可在Si 表面发现很多凸起的点,命名为纳米点。这些纳米点在硅MOS 结构和器件中会增加界面态,形成潜在的可靠性风险。此外,在大注量的重离子辐射下,使用透射电子显微镜可以看到在Si 和SiO2之间有清晰明显的薄过渡层[20]。通过测量EDX 能谱,发现Si ∶O 原子比发生了变化,这种变化可归因于Si—O 键断裂后Si 向界面迁移。该氧化层SiOx(1 作者团队自研的VDMOS 器件在经过单粒子辐射后其栅氧化层出现软击穿现象,且首次观察到在漏极电压作用下,VDMOS 体二极管的反向I-V曲线发生蠕变。随着环境温度的降低,I-V曲线发生蠕变时所需的漏极电压增大,且从蠕变状态到稳定所需时间增加。本文将对该现象进行描述和机理解释,并提出基于界面态、中性空穴陷阱[21-22],包括空穴激发、多能级空穴跃迁和俘获[23-24]、能带隧穿过程的空穴迁移模型,通过漏极应力实验和温度实验说明了模型的合理性。 VDMOS 器件结构和工艺由作者所在团队自主设计,并通过国内6 寸代工平台采用平面工艺制造,器件剖面结构示意图如图1 所示。VDMOS 制造采用后栅氧工艺,首先使用掩膜版通过离子注入和高温退火分别形成P-body 和N+源区,而后低温(<1000 ℃)生长栅氧化层,保证栅氧化层质量,降低界面态。栅氧化层采用干法和湿法的混合方式,厚度为80 nm。VDMOS 器件的版图和实际制造的芯片表面图如图2所示。VDMOS 芯片的面积为6.6 mm × 4.9 mm,使用TO-254 金属封装。测试显示,VDMOS 的阈值电压典型值为3.5 V,击穿电压不低于300 V。 图1 VDMOS 器件剖面结构示意图Fig.1 Cross-section diagram of the VDMOS 图2 (a)VDMOS 器件版图;(b)VDMOS 芯片表面图Fig.2 (a) Layout of the VDMOS;(b) Surface image of the VDMOS chip 随机挑选5 只VDMOS 器件进行单粒子辐射实验,辐射实验在中科院近代物理研究所的重离子加速器进行[25-26],辐射粒子为Ta 粒子,能量为1.5 GeV,线性能量传输LET 为80 MeV·cm2/mg,辐射粒子的注量率为5000 粒子/(cm2·s),总量为106粒子/cm2。在单粒子辐射过程中,栅极与源极短接,漏极电压为300 V,保证器件在单粒子辐射时工作在阻断状态。SER 实验前后,所有器件均使用JUNO DTS-2000 静态参数测试仪进行测试,测试方式为脉冲测试法。 SER 实验完成后,其中4 只VDMOS 器件静态特性,包括击穿电压、导通电阻、阈值电压、栅-源极漏电流和零栅偏漏-源极漏电流均在产品规格书范围内,且与辐射前数据相比无变化。而剩余一只VDMOS 器件的栅-源间漏电流明显超过最大值(±100 nA),但其击穿电压、阈值电压、导通电阻和零栅偏漏-源极漏电流均正常。若VDMOS 发生SEB 或(和)SEGR 失效,器件的三端均会短路,而不会是只有某个参数发生退化,因此栅-源极漏电流增大与GOI 相关。为进一步探究失效情况,使用晶体管图示仪DW4822 测试该失效器件,测试采用直流模式。 晶体管图示仪测试时,漏极浮空,测试栅极和源极之间正反向的漏电流,测试的IGS-VGS曲线如图3 所示。栅-源极漏电流IGSS和源-栅极漏电流ISGS在电压远低于栅氧化层击穿电压(>20 V)的情况下显著增大。除了栅-源极漏电流外,晶体管图示仪在测试VDMOS体二极管的阻断特性时发现IL-VDS曲线蠕变的特殊现象。当栅极浮空,漏-源极电压(VDS)持续增大,室温下当VDS达到35 V时,漏电流开始增大,此时保持VDS不变,IL-VDS曲线开始蠕变,图4(a)~(f)记录了IL-VDS曲线在不同时间的位置,并最终在t=6.23 s 时稳定,体二极管漏电流为13 μA,形成类似电阻型的曲线,而正常体二极管的阻断特性与VDMOS 的阻断特性一致,是一个硬击穿的曲线图。 图3 (a) 栅-源极漏电流IGSS;(b) 源-栅极漏电流ISGSFig.3 (a) Gate-source leakage current IGSS;(b) Source-gate leakage current ISGS 图4 VDMOS 体二极管反向I-V 曲线蠕变现象: 在VDS增加到35 V 时IL-VDS曲线发生变化,漏电流随时间逐渐增大。最终, IL-VDS曲线稳定。(a)~(f)显示了在不同时间点VDMOS 体二极管的IL-VDS曲线图。(a) t=0 s;(b) t=2.24 s;(c) t=3.68 s;(d) t=4.52 s;(e) t=5.16 s;(f) t=6.23 sFig.4 Walk-in phenomenon of reverse I-V curve of the body diode in the VDMOS. IL-VDS curve begins to walk-in once VDS is increased to 35 V,the leakage current increases gradually with stress time.Finally,the curve stabilizes.(a) -(f) show IL-VDS curves of the body diode in VDMOS at different time.(a) t=0 s;(b) t=2.24 s;(c) t=3.68 s;(d) t=4.52 s;(e) t=5.16 s;(f) t=6.23 s 根据测试结果,器件栅-源极间存在漏电流表明氧化层可能有损伤,这会导致体二极管在阻断状态下产生漏电流。此外,根据VDMOS 器件结构,体二极管P-body/N-Epi 结若存在缺陷也会导致漏电流的产生。对于第二种漏电机制可以通过VDMOS 器件本身的阻断特性来甄别。VDMOS 器件的阻断特性由Pbody/N-Epi 结的特性决定,如果该PN 结有损伤缺陷,则VDMOS 器件的阻断特性也会有类似的蠕变现象。图5 为VDMOS 器件在不同温度下阻断特性的IL-VDS曲线。由图可知,室温下VDMOS 的击穿电压为410 V,与Juno 静态参数测试仪脉冲法测试结果一致,且器件为硬击穿,在击穿前没有明显漏电流,且随着环境温度的降低,击穿电压降低,验证了击穿电压是正温度系数,符合PN 结击穿特性机理。随着温度的降低,硅原子晶格振动变弱,载流子的声子散射减小,导致载流子的平均动能增加,从而增强了碰撞电离过程,使得VDMOS 器件击穿电压降低。因此可以排除P-body/N-Epi 结的损伤缺陷原因,确认PN 结在单粒子辐射后依然是完好的。VDMOS 体二极管的漏电流是由PN 结周围的氧化层中存在的电流通路产生的。 图5 在不同环境温度(TA)下VDMOS 的击穿电压。测试条件: 栅源极短接,增大漏极电压。(a) TA=294 K;(b) TA=273 K;(c) TA=248 K;(d) TA=233 KFig.5 Breakdown characteristics of the VDMOS at various ambient temperature (TA).Test condition: gate-source shorted and drain voltage increased.(a) TA=294 K;(b) TA=273 K;(c) TA=248 K;(d) TA=233 K 为了进一步探究VDMOS 体二极管I-V曲线蠕变现象,对单粒子辐射后VDMOS 体二极管的漏电流产生机制提出空穴迁移模型,并通过辅助实验验证。 通过测量VDMOS 的击穿特性,排除了PN 结中存在缺陷的可能性。所以氧化层缺陷是漏电流产生的源头,而氧化层中漏电流是由载流子通过缺陷能级的跃迁产生的[14-16]。 单粒子辐射时,高能粒子轰击VDMOS 将与硅、氧原子以及其他杂质原子(如C、Mg)碰撞,产生核阻止和电子阻止。电子阻止会使得高能粒子在VDMOS器件中的入射径迹上产生大量电子空穴对,在漏极电压作用下,载流子相互复合和抽取过程使得器件漏源极间形成瞬时浪涌电流。若该电流导致VDMOS 寄生的NPN 管开启,便会使器件进入闩锁状态而发生SEB现象。同时,漏极电压会使VDMOS 器件中产生的电子空穴对分离,空穴会在栅氧化层下聚集。若积累的空穴在栅氧化层中产生的电场超过氧化层的临界电场,则会发生SEGR 现象。而由前述测试可知器件未被烧毁,也未发生完全的栅氧化层破坏。因此电子阻止不是该失效VDMOS 器件产生漏电流的原因。 核阻止会在硅半导体和氧化物中产生空位、陷阱等缺陷。在硅半导体材料和氧化层中,晶格原子的位移阈值为10~25 eV,高能粒子入射产生的核阻止使晶格原子在高能粒子入射方向上发生位移,形成空位缺陷。由于入射粒子能量较大,其在入射方向上会使得一系列晶格原子产生位移,同时入射的高能粒子与位移原子会产生非弹性碰撞,非弹性碰撞的位移原子沿不同方向移动并继续碰撞晶格原子产生空位,从而使得高能粒子在其入射路径上产生空位团簇陷阱。高能粒子在穿越Si-SiO2界面能轻易破坏Si—O键,形成Si悬挂键,增加了Si-SiO2界面处的界面态密度。SiO2中一些缺陷可以捕获空穴可称为中性空穴陷阱。同时高能粒子在硅片中的非弹性碰撞会导致部分Si 原子反弹到Si-SiO2界面形成纳米点,这便导致更大的界面态[17-20]。因此,本文提出了一种基于界面态、中性空穴陷阱,包括空穴激发、空穴多级俘获和能带隧穿机制的空穴迁移模型用以说明VDMOS 体二极管I-V曲线的蠕变。空穴迁移产生漏电流的过程如图6(a)所示,可将整个迁移过程分为三个阶段,分别如图6(b)、6(c)和6(d)所示。 图6 空穴迁移模型。(a) 空穴迁移过程;(b) 阶段Ⅰ: 空穴激活;(c) 阶段Ⅱ: 空穴跃迁;(d) 阶段Ⅲ: 空穴隧穿Fig.6 Hole migration model.(a) Hole migration process;(b) Process Ⅰ: hole exciting;(c) Process Ⅱ: hole transition;(d) Process Ⅲ: hole tunneling 阶段Ⅰ: 空穴激发。漏极加压时,Si-SiO2界面处空穴获得能量,随着VDS的增大,当空穴获得的能量大于其自身的激活能(EA)时,空穴被激发从界面处跃迁至SiO2层中的中性空穴陷阱; 阶段Ⅱ: 空穴多级跃迁和俘获。漏极电压VDS在氧化层中产生的电场使得空穴在氧化层中沿着电场方向在中性空穴陷阱之间跃迁; 阶段Ⅲ: 空穴隧穿。空穴通过电场积累的能量在金属源极与氧化层界面处产生隧穿,形成VDMOS 体二极管的漏电流。 空穴本身具有动能(EK)和势能(EP),并能通过外加电场获得能量(EF)。当EK+EP+EF>EA,空穴发生跃迁。空穴具有的动能和环境温度相关,势能和缺陷能级位置有关。因此根据空穴迁移的过程,可以得到单粒子辐射下VDMOS 体二极管反向漏电流的表达式: 式中:K是损伤系数;NT(LET,TOX,EOX(VDS))是单粒子辐射下氧化层中的中性空穴陷阱密度,它与线性能量转移(LET)、氧化层厚度(TOX)和单粒子辐射时漏极电压VDS在氧化层中产生的电场(EOX(VDS))有关;LOX是氧化层的宽度;τin(EOX⊥(VDS),TA)和τtun(EOX‖(VDS),TA)分别表示空穴从Si-SiO2界面跃迁进入栅氧化层和从栅氧化层中隧穿至金属源极所需的时间;是空穴穿越氧化层所需的总时间,它与空穴迁移率(μp)、漏极电压在氧化层中产生的横向电场(EOX‖(VDS))、空穴寿命(τp)、空穴的横向位置(Lx)有关。上述三个时间参数代表了空穴迁移的三个物理过程,它们均受环境温度(TA)和漏极电压(VDS)的影响。 通过分析空穴迁移的过程,影响空穴跃迁的关键外部条件是所加漏极电压在硅半导体和氧化层中产生的电场和环境温度。漏极电压和环境温度决定了空穴跃迁的总量和迁移速率。单粒子辐射在氧化层中形成缺陷,而缺陷密度决定了可俘获的空穴数量的上限。此外,在漏极电压和环境温度一定时,可以被激发的空穴总量是有限的,这使得蠕变的I-V曲线最终稳定。因此,为了验证上述空穴迁移模型的合理性,设计了温度实验和漏极电压应力实验,通过测试VDMOS 体二极管漏电流(IL)值和IL-VDS曲线开始产生蠕变时的漏极电压(VK)值的变化以及达到一定漏电流值所用应力时间(t)来分析说明。 图7 为在不同环境温度(TA)下,失效的VDMOS器件体二极管发生蠕变后最终稳定时的IL-VDS曲线。测试条件为: VDMOS 栅极浮空,在漏极缓慢增大VDS,在器件开始发生蠕变时停止加压,曲线稳定后获得如图7(a)~(c)图形。由测试图形可知,随着环境温度的降低,发生蠕变时的电压值(VK)单调增大,分别为35,80 和400 V。当环境温度降低,空穴激活能增大,空穴需要从漏极电压产生的电场中积累更多能量才能形成跃迁。因此,可以预见当环境温度足够低时,空穴跃迁所需要的漏极电压将大于VDMOS 器件本身的击穿电压,此时PN 结将首先发生雪崩击穿,体二极管的IL-VDS曲线将不会产生蠕变。 图7 在不同环境温度(TA)下VDMOS 体二极管反向I-V 曲线开始蠕变时的转折电压(VK)的变化图。(a) TA=294 K;(b) TA=273 K;(c) TA=248 KFig.7 Variation diagrams of the knee voltage (VK) when the I-V curve of the body diode in the VDMOS begins to walk-in at various ambient temperatures (TA).Test condition: gate-source shorted and drain voltage increased.(a) TA=294 K;(b) TA=273 K;(c) TA=248 K 图8 展示了在恒定的漏极电压VDS=50 V下,体二极管的反向漏电流(IL)随环境温度(TA)变化的曲线图。可以看出,低温下的dIL/dt远小于常温下的dIL/dt。在低温下,VDMOS 体二极管反向漏电流达到指定电流值所需的应力时间比在相对更高温度下更长。如图8 所示,在273 K 和240 K 时达到4 μA 的漏电流的时间消耗(t)分别为11.1 s 和180 s。此外,低温下,IL-VDS曲线蠕变后最终稳定的漏电流值随着环境温度的降低而减小。如图,在294 K 和240 K时,蠕变曲线稳定后最大漏电流分别为20 μA 和4 μA。在较低的环境温度下,空穴激活能增大,在同样的漏极电压下,被激发的空穴总量越少,空穴迁移产生的漏电流也越小。而环境温度越高,激活能越低,空穴在氧化层中可迅速地穿越,可更快地形成漏电流,同时依据式(1),更快的氧化层穿越速率会形成更大的漏电流。 图8 在VDS=50 V时,VDMOS 体二极管漏电流(IL)在不同环境温度(TA)下随时间(t)的变化曲线Fig.8 The leakage current(TL) of the body diode in the VDMOS varies with stress time (t) when VDS=50 V at various ambient temperatures (TA) 图9 展示了在室温TA=294 K下,体二极管的反向漏电流(IL)随漏极电压(VDS)变化的曲线图。可以看出,随着漏极电压的增大,漏电流变化率dIL/dt也随之增大,且IL-VDS曲线蠕变后最终的漏电流值同样增大。更大的漏极电压VDS,意味着半导体和氧化层中更大的电场强度,空穴可以获得更多能量而被激发,更多被激发的空穴在更高的电场下形成更大的漏电流。同时更强的电场强度也加快了受激发的空穴的迁移速率(ν=μp·E),使得漏电流更快形成。 图9 在TA=294 K时,VDMOS 体二极管漏电流(IL)在不同漏极电压(VDS)下随时间的变化曲线Fig.9 The leakage current (IL) of the body diode in the VDMOS varies with stress time (t) when TA=294 K at various drain voltages (VDS) VDMOS 体二极管的反向I-V曲线发生蠕变现象在实验中首次被发现,本文对I-V曲线蠕变的现象进行了研究分析。引起反向漏电流的原因是单粒子轰击在氧化层中带来晶格损伤和价键断裂,产生诸多缺陷,给载流子跃迁提供了电流通道。为解释反向漏电流的形成机制,提出了基于界面态、中性空穴陷阱,包括空穴激发、空穴多级俘获和能带隧穿机制的空穴迁移模型。设计并实施了环境温度实验和漏极电压应力实验以观察体二极管漏电流的变化情况。通过实验可以验证,空穴受激发的总量与环境温度相关,影响最终漏电流形成的速度以及漏电流值的大小。且可以预见在足够低的环境温度下,可以消除体二极管反向I-V曲线的蠕变现象。漏极电压的不同改变了半导体和氧化层中的电场,导致空穴获得的能量有差别,更高的漏极电压可以激发更多界面空穴,并加快空穴的迁移速率,从而使得漏电流更快产生,同时导致更大的漏电流。实验测试现象可以通过单粒子辐射下体二极管漏电流的表达式来解释,证明空穴迁移模型和漏电流表达式的合理性。这为功率器件在单粒子辐射后有关漏电流失效问题的解决提供了可靠的模型方案。1 蠕变现象
1.1 器件结构和辐照实验
1.2 失效现象和分析
2 空穴迁移模型
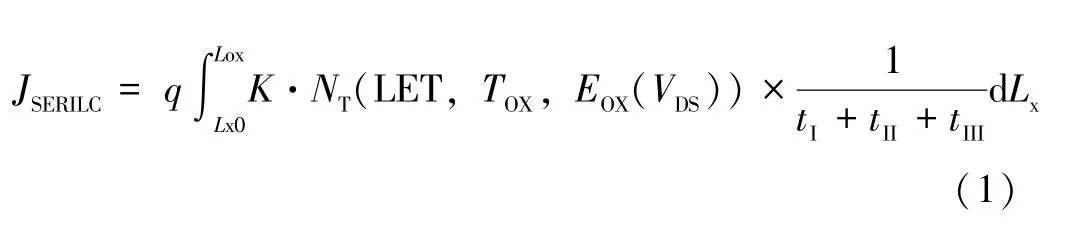
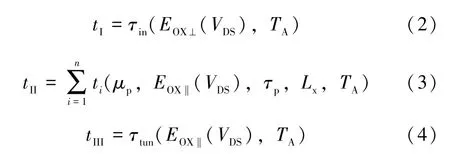
3 实验验证

4 结论
