利用柯西不等式证明一类分式不等式的升幂技巧

山东省邹平双语学校(256200) 姜坤崇

利用柯西不等式(或其变形式)可以证明大量的不等式,特别是分式不等式,但对于不少分式不等式而言,若直接使用柯西不等式(或其变形式)证明则常常会中途搁浅,这时我们不妨采用一种技巧来试一试,有可能化“不可能”为可能.这种技巧即将分式的分子和分母同乘以分子的幂底数的某一次方,使得分子的幂的次方高于原幂指数(一般升为偶数次方),从对下面的不等式证明的一些例题中可以看出,这种先升幂后用柯西不等式证明分式不等式的技巧屡试不爽.

一、证明无条件约束不等式

这类不等式除了对变元有正数的要求外无其它等式条件约束.

例1已知a,b,c是正数,求证:

由于以上最后一个不等式不成立,故此证法搁浅.

虽然这个“证明”没有完成,但我们不能轻易否定以上的证题思路,对于解决某些问题有时候不是因为基本思路出了问题,而是还没有找到正确的解题方法和技巧.事实上,只要我们将所证不等式的每一个分式的分子、分母的幂都由二次升为四次,并沿着以上同样的思路就可“柳暗花明又一村”,从而给出不等式的正确证明.

证明由柯西不等式的变形式得

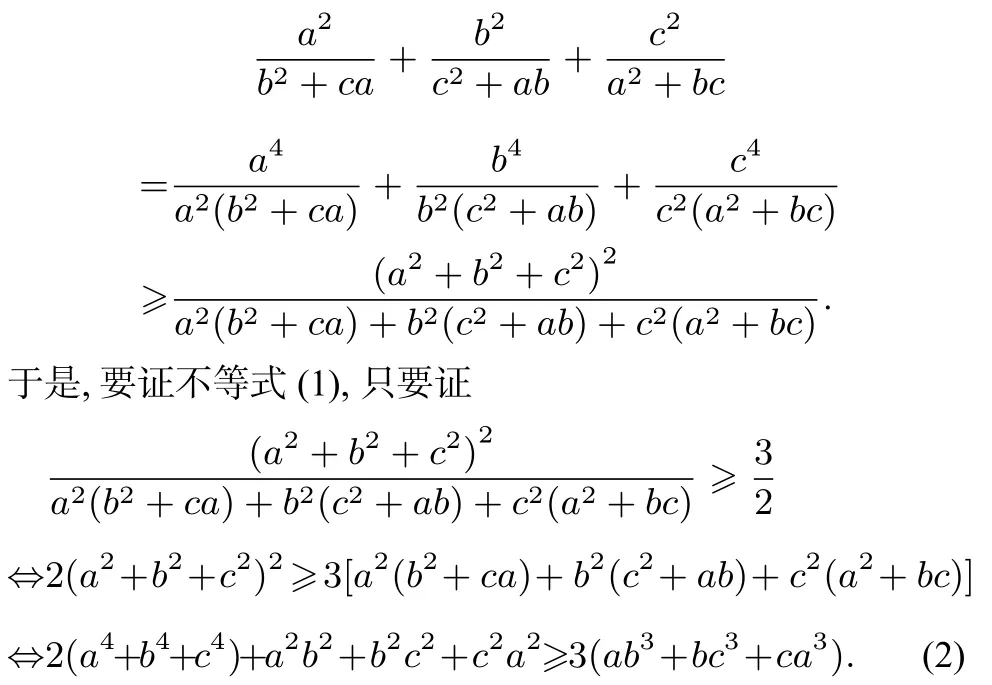
由二元均值不等式得,b4+a2b2≥2ab3,c4+b2c2≥2bc3,a4+c2a2≥2ca3,以上三个不等式相加得

又由4 元均值不等式得,a4+3b4≥4ab3,b4+3c4≥4bc3,c4+3a4≥4ca3,以上三个不等式相加然后两边约去4得

(3)+(4)即得(2)式,所以不等式(1)得证.

例2(自编题)已知a,b,c为正数,求证:

分析由于不等式(5)与不等式(1)很类似,因此同证明不等式(1)一样,若不将不等式的每一个分式的分子、分母的幂升级而直接使用柯西不等式的变形式则不能完成其证明,以下我们仿照证明不等式(1)的思路与方法来完成对不等式(5)的证明.

证明由柯西不等式的变形式得

于是,要证不等式(5),只要证

⇔(2)式,所以不等式(5)得证.

例3 (自编题)已知a,b,c是正数,求证:

证明由柯西不等式的变形式得

于是,要证不等式(6),只要证

仿(2)式的证明可证(7)式成立,从而不等式(6)得证.

而由柯西不等式的变形式得

例5 (自编题)设a,b,c>0,求证:

二、证明一类条件不等式

这类条件不等式,是指不等式中含有xyz=1 等约束条件的不等式.

由柯西不等式的变形式得

于是,要证不等式(8),只要证

由柯西不等式的变形式得

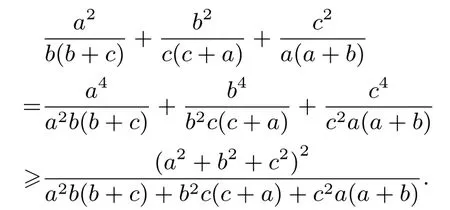
于是,要证不等式(9),只要证

(11)×2+(12),即得(10)式,从而不等式(9)成立,因此原条件不等式获证.

由柯西不等式的变形式得

于是,要证不等式(13),只要证

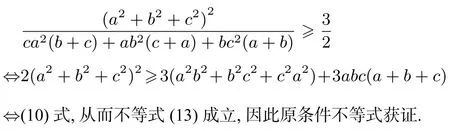
三、证明含参数的不等式

以下三例中的不等式,都是含有参数λ的不等式.

例9(《中等数学》2015 年第10 期奥林匹克问题高446(由笔者提供))设a、b、c>0,λ≥1.证明:

故式(15)成立,从而不等式(14)得证.

说明不等式(14)是《数学通报》数学问题1818 中的如下不等式的加权推广:

证明由柯西不等式的变形式得

于是要证原不等式成立,只需证:

说明在例10、11 的不等式中令λ=1 可分别得文献[2]中的如下问题1、2 中的不等式,所以例10、11 中的不等式分别是这两个不等式的加权推广.