对一道预赛试题中定值问题与最值问题的探究

湖北省恩施州教育科学研究院(445000) 周威

一、基于试题情境的性质探究

例1 (2022 年5 月重庆市预赛试题)设F是双曲线Γ:x2−y2=1 的左焦点,经过F的直线与Γ 相交于M,N两点.

(1)若M,N两点都在双曲线的左支上,求∆OMN面积的最小值;

(2)是否存在x轴上一点P,使得为定值? 若存在,求出点P的坐标;若不存在请说明理由.

此题以最简单的双曲线方程、以最常规的过焦点的直线为载体,第一问考查三角形面积的在圆锥曲线中的通性通法;第二问基于探究性问题,考查学生发现问题、解决问题的能力,以及处理为定值时的化归转化思想.此题从圆锥曲线的最基本的元素和最基本的设问出发,落脚在三角形面积最值问题和圆锥曲线中常规的定点定值问题,从而十分具有探究价值,作为解析几何专题的高考备考也十分适用.

问题1基于例1 中两个提问,若一般化双曲线的方程,是否可以抽象出双曲线中的一个基本性质?

事实上,经过探究,有以下结论.

证明(1)设F(−c,0),则直线MN的方程为x=my−c,将直线方程代入双曲线方程得(b2m2−a2)y2−2b2cmy+b4=0,设M(x1,y1),N(x2,y2),则

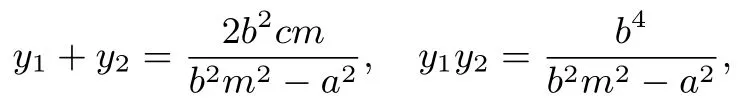
因为M,N两点都在Γ 左支:

同理,若F是右焦点,第(1)、(2)问由于对称性,结论类似,请读者完成.

二、基于定值性质的推广探究

我们知道,很多时候圆锥曲线都有相对统一的性质,那么依然设F是圆锥曲线Γ 的左焦点,经过F的直线与Γ 相交于M,N两点,自然有如下问题:

问题2在椭圆和抛物线情境中,是否也存在x轴上一点P,使得为定值?

经过探究,类比性质1 有如下性质:

性质3 的证明很容易(略).

三、基于形式统一性的变式探究

问题3若M,N是一条过圆锥曲线Γ 某焦点的直线与Γ 相交时的任意两点,O为原点,那么∆OMN面积有无最值? 如果原点O不能满足条件,受例1 中第(2)问的启发,那么是否在x轴上存在另一点P使得∆PMN面积存在最值.

由性质1 中的讨论可知其并无最值! 同理可得椭圆、抛物线的情形,也没有最值! 从而必须在x轴上寻找另一点P,那么对于圆锥曲线来说,点P是否存在形式特殊性和统一性呢?通过探究,有如下性质和结论:

证明设直线MN的方程为x=my −c,将直线方程代入双曲线方程得(b2m2−a2)y2−2b2cmy+b4=0,设M(x1,y1),N(x2,y2),则

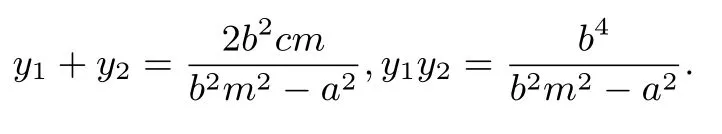
简证设直线MN的方程为x=my −c,M(x1,y1),N(x2,y2),将直线方程代入椭圆方程得(b2m2+a2)y2−2b2cmy −b4=0,则

性质6设F是抛物线Γ:y2=2px(p >0)的焦点,过点F的直线交Γ于M,N两点,直线x=−与x轴交于点P,记∆PMN的面积为S,则S≥p2.

性质6 可类比证明(限于篇幅,过程略).显然以上性质都是基于P点是圆锥曲线准线与x轴的交点的统一性与特殊性,出现了三角形面积最值情形,但值得一提的是性质5的探究中要进行分类讨论,这也正是探究问题的乐趣所在.