基于参数辨识的半导体激光器温度自动控制

高华兴

(中国空间技术研究院，北京100094)

0 引言

随着科技的不断革新与进步，半导体激光器的设计更加精细化，具备了低能效、小体积和轻量化等优势[1]，在信息传输、医疗卫生和工业等领域均有重要用途。半导体激光器对温度变化具有较强的敏感性[2]，运行温度改变致使半导体激光器内部材料折射率发生变化，进而改变其输出功率及波长。当半导体激光器运行温度增大，会使其内部结构遭受破坏，降低其使用寿命[3]。因此，如何对半导体激光器温度进行有效控制具有重要意义。

张安迪等[4]针对半导体激光器温度变化对其正常运行产生的影响，设计了以单片机为主控单元，以热电制冷器、加热器为基础单元的温度控制系统，通过论域可变的PID控制方法实现其温度的精准控制，但该方法受PID控制参数影响较大，致使温度控制准确度存在一定偏差；程前等[5]根据半导体激光器电流负反馈特性，通过恒流源电路、继电保护电路实现半导体激光器稳定电流控制，并利用温控系统控制完成其温度控制目标，该方法因未解决半导体激光器的一阶纯滞后环节，导致控制后的温度仍在较大范围内变化。

因此，本文提出基于参数辨识的半导体激光器温度自动控制方法，在构建半导体激光器的参数辨识模型的基础上，利用遗传算法对PID参数进行实时调节，以满足半导体激光器温度变化量对PID参数的自整定需求，以此达到精准控制温度的目标。

1 半导体激光器温度自动控制方法设计

1.1 半导体激光器温度控制原理

1.1.1 温度对半导体激光器参数的影响

半导体激光器参数受温度的影响，表现在以下2个方面：

a.温度值过大，将迅速降低半导体激光器的输出功率，对其使用寿命影响较大。

b.半导体激光器在运行时，其输出波长受运行电流、温度的影响较大，温度与输出波长的变化成正比关系[6]，温度越高，波长越大，为确保半导体激光器输出波长处于稳定状态，需不断调节其输出波长，使温度在适当区间内变化，这是一种非常有效的温度控制措施。

1.1.2 半导体激光器温度控制原理

为实现半导体激光器温度的有效控制，首要任务是对采集温度和设定温度间的误差进行预估，将误差预估值输入到PID中，通过PID控制算法实现半导体激光控制量预测，将预测结果发送至电流驱动TEC，在对半导体激光器制热或冷却时，通过感应对应电路的温度变化，调节电路电流，使半导体激光器温度在适合区间内变化，以确保半导体激光器平稳运行。

1.2 半导体激光器温度控制系统的总体结构

图1为半导体激光器温度控制系统的总体框架。在半导体激光器温度控制系统中，主要控制单元为TMS320F2808芯片，半导体激光器温度控制原理是：利用温度传感器测量半导体激光器实时温度，并将其变换为温度信号，利用放大电路对其进行放大操作后，输入到数字信号处理(digital signal processing，DSP)主控芯片，通过其ADC模块实现温度信号的A/D转换，获取数字量，利用DSP主控制器的控制算法对其进行控制，获得控制量，并确定PWM波的占空比，以PWM波作为半导体激光器温度控制系统的输出，通过功率开关促使陶瓷加热片工作，实现半导体激光器的温度控制。

图1 半导体激光器温度控制系统的总体框架

1.3 半导体激光器温度控制的数学模型

在该系统的支持下，构建半导体激光器温度控制的数学模型，以此实现相关控制目标。

设定在时间点t，陶瓷加热片散发的总热量为Qt，对于半导体激光器，若其温度维持于固定值时，可确定Qt由2部分构成[7]，分别为Q1和Q2，Q1为此刻半导体激光器的热量，Q2为陶瓷加热片自身消散的热量。此时，Qt为

(1)

C为半导体激光器比热容；T为半导体激光器的温度；T1为环境温度；R为阻值。以T作为对比，当T1很小时，可不予考虑。则Qt为

(2)

经过拉普拉斯变换后，可得

Qt(S)=C·s·T(S)+R-1T(S)

(3)

本文系统的输出结果为U(S)，依据其控制原理，若U(S)、Qt(S)二者为正比关系，则当温度传感器采集半导体激光器的实时温度时存在时间延迟，同时陶瓷加热片在温度传递时，同样具有容积延迟，在二者的共同作用下，导致其温度控制信号Y(S)与测量温度无法保证同步，由此，该系统的传递函数[8]为

(4)

K为系统增益，K=kR；T为时间常数，T=RC。通过测试得出K=1.8、T=100、τ=2。此时，则存在

(5)

式(5)是对半导体激光器一阶纯滞后环节的描述。

1.4 基于参数辨识的半导体激光器温度控制方法

1.4.1 半导体激光器等效参数模型

半导体激光器的热介质温度改变的情况可通过公式(6)和式(7)进行描述[9]，即：

(6)

(7)

式(6)和式(7)为常微分方程。其中，Ti(t)为环境温度；Tm(t)为t时间点半导体激光器的温度；Ca、Cm分别为环境、半导体激光器的等效热容；Rm为环境与半导体激光器间的等值热阻；Q(t)为陶瓷加热片的热功率。

1.4.2 建立参数辨识模型

热介质具有热传递、热存储的特点，本文通过式(6)和式(7)的等值参数反映热介质这一特性，因等值参数无法直接采集，造成半导体激光器温控负荷分析难度较大，因此本文通过获取半导体激光器的离散运行数据，建立参数辨识模型。

陶瓷加热片依据所设温度及环境温度的情况进行加热或冷却操作，其运行功率为

(8)

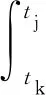
P为额定功率；η为其能效比；Ts为半导体激光器的期望温度；Tδ为半导体激光器的温度控制裕量；s为开关状态，0、1为其值，分别代表停止、开启状态；ε为温度测量周期。根据式(6)和式(8)，可确定tk～tj时间段内半导体激光器的温度变动范围，将其描述为

Ti(tj)-Ti(tk)=

(9)

令Cm≫Ca，Tm值固定不变，由此，可将式(9)简化为：

Ti(tj)-Ti(tk)=

(10)

(11)

β1、β2、β3为半导体激光器温度控制参数，并对其进行计算。采集半导体激光器的运行数据，ε为各次采样相隔周期，对式(9)进行离散化处理[10]，搭建半导体激光器参数辨识模型，其表达式为：

Yj=β1Aj+β2Cj+β3Dj

(12)

(13)

利用温度传感器、气象数据可获得式(12)和式(13)中的Yj，通过陶瓷加热片的工作数据可得到s(t)，由此可确定Aj、Cj、Dj。

1.4.3 模型最佳预估量

由Gauss-Markov定理可知，通过最小二乘法获取的预估量最为精准、无误差[11]，因此，本文采用该方法对半导体激光器的温度控制参数进行运算。

tk、tj为2个不同时刻，通过对其进行选择，可获得数组样本数据，运用最小二乘法确定参数辨识目标函数，其表达式为

X(β1,β2,β3)=(Yj-β1Aj-β2Cj-β3Dj)2

(14)

在对半导体激光器参数进行辨识时，所用样本数据总数量为z，为实现半导体激光器的最优温度控制结果，需对目标函数X取极小值，对于半导体激光器温度控制参数β1、β2、β3，其最小二乘预估量需符合条件为

(15)

β1、β2、β3为待求参数，通过运算获取其值，由此可确定半导体激光器参数辨识模型的最佳预估量。

1.4.4 半导体激光器的PID温度控制

在确定半导体激光器的最佳预估量前提下，通过对PID控制器参数进行整定，实现半导体激光器的温度控制。在对半导体激光器温度进行PID控制时，主要由3部分构成[12]，分别为：

a.比例作用，反映了半导体激光器的往期温度控制对当下状态的影响。

b.积分作用，是对半导体激光器往期温度控制总体效果的描述。

c.微分作用，是对将来半导体激光器温度控制目标的描述。

基于PID控制的半导体激光器温度控制目标是使控制偏差最小化，并降低外来因素对半导体激光器的干扰。其首要步骤是确定半导体激光器的温度控制的参数模型，通过基于规则的自整定法获取PID控制器比例、积分和微分参数[13]，分别为KP、KI、KD。PID控制的表达式为

Δu(k)=YjKP(e(t)-e(t-1))+

YjKPe(t)TD(TI)-1+

YjKP(e(t)-2e(t-1)+e(t-2))

(16)

TI、TD分别为积分、微分时间常数；e(t)为控制误差。

1.4.5 基于遗传算法的最优PID控制参数选取

在采用PID控制器对半导体激光器温度进行控制时，其参数KP、KI、KD是衡量半导体激光器温度控制性能优劣的重要因素[14]，因此，本文利用遗传算法对上述参数进行优化，获取最佳参数值。以PID控制参数KP、KI、KD作为变量，将J作为目标函数，可将其描述为

(17)

e(t)为半导体激光器温度控制系统误差；对于PID控制器，u(t)为其输出结果，tr为升温时间，ω1、ω2、ω3分别为权重。对控制参数进行编码，将其描述成二进制形式。设定参数P∈[Pmin,Pmax]，b为二进制数，其位数为m，参数P的二进制描述表示为

P=Pmin+(m2-1)-1bPmax

(18)

对于参数KP、KI、KD，分别采用二进制形式对其描述，通过将各二进数相连实现参数编码[15]。根据适应度值确定遗传个体，个体选择操作可描述为

(19)

fi为第i个遗传个体适应度值；M为种群规模；ps为选择概率。

假设pc为交叉概率，pm为变异概率，二者可通过单点交叉法获取，其公式为：

(20)

(21)

k为迭代次数，k∈[1,kmax]；kmax为迭代最大值。运用遗传算法对PID参数进行优化，PID控制器可描述为

(22)

利用遗传算法确定最优PID控制参数流程为：

a.对参数KP、KI、KD的变动区间进行预估，并对其进行编码。

b.对种群进行初始设置，种群规模N。

c.通过解码确定PID控制参数，建立J函数，获取适应度值。

d.通过选择、交叉、变异操作，确定子代种群。

e.判断迭代次数是否达到最大值，若是则进行解码操作，输出最优PID控制参数选择结果；返之，则退回到步骤b～步骤d，直至满足迭代条件，算法结束。

最优PID控制参数选取流程如图2所示。

图2 最优PID控制参数选取流程

2 实验分析

以某半导体激光器为对象，利用MATLAB模拟其运行状态，采用本文方法对其温度进行控制，验证该方法的温度控制效果。遗传算法初始种群规模60，交叉概率取值0.80，变异概率取值0.04，PID控制各参数的取值区间分别为KP∈[0.08,8.00]、KI∈[0.08,8.00]、KD∈[0,1.00]，各权重取值为ω1=1.00、ω2=0.03、ω3=2.40，最大迭代次数为80。

设定环境温度为21 ℃，为验证本文方法的温度控制效果，设定2种温度控制方案，分别为：

a.方案1:在高于环境温度条件下实施半导体激光器温度控制实验，对陶瓷加热片加热，设置其温度为30 ℃，温度监测时间为2 h，温度采集周期设为1.5 min。

b.方案2:在低于环境温度条件下开展半导体激光器温度控制实验，对陶瓷加热片进行降温处理，温度设置为15 ℃，温度监测时间、采集时间同方案1一致。

2种方案下半导体激光器温度控制结果如图3、图4所示。

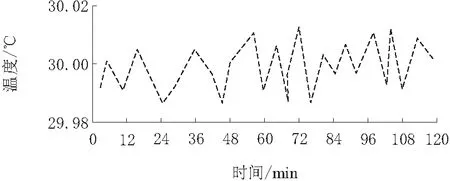
图3 方案1的温度控制分析

图4 方案2的温度控制分析

分析图3可知，在高于环境温度的情况下，采用本文方法对半导体激光器温度进行控制，半导体激光器温度可控制在30 ℃左右，温度波动范围不超过0.02 ℃，实验结果表明，本文方法在高于环境温度下，可实现半导体激光器温度的有效控制，且控制精度较高。

由图4可知，本文方法在低于环境温度条件下，对半导体激光器温度控制仍具有较好效果，控制后温度可达到预期值，且温度变化范围不足0.01 ℃。由图3和图4实验结果得出，本文方法对半导体激光器温度控制效果好。

半导体激光器温度对其输出波长具有较大影响，当半导体激光器温度处于稳定状态时，其发光光谱波形将呈现出平稳走势，因此本文通过半导体激光器的发光光谱测试实验，分析本文方法的温度控制效果，测试在1 h内完成，每次测试间隔5 min，实验结果如图5所示。

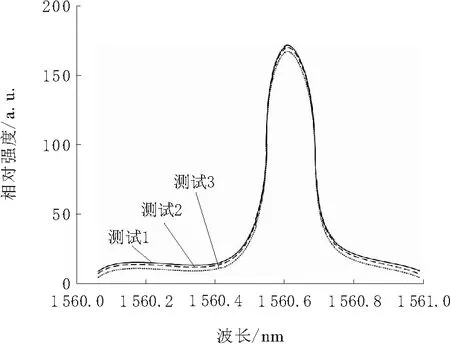
图5 半导体激光器发光光谱分析

分析图5得出，各次半导体激光器发光光谱测试所得光谱图均保持相同变化规律，且基本重合，说明光谱呈现稳定走势。实验结果表明，本文方法的温度控制效果更好。

设置半导体激光器温度为20 ℃，分别利用文献[4]方法、文献[5]方法及本文方法对半导体激光器温度进行有效控制，通过分析各方法的温度控制结果，验证本文方法的应用性能，实验结果如图6所示。

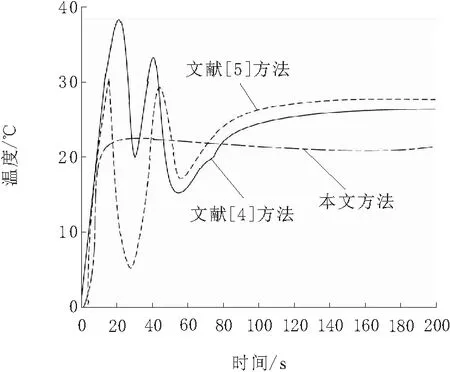
图6 各方法的温度控制结果

分析图6可知，应用文献[4]方法、文献[5]方法控制半导体激光器温度时，在控制的前60 s其温度波动幅度较大，随后温度才开始慢慢趋于平稳，且文献[5]方法的控制后温度高于文献[4]方法，二者均未达到设定温度；经本文方法控制后，半导体激光器温度可较快趋于稳定，且控制后温度基本达到设定值。实验结果表明，本文方法可有效控制半导体激光器温度，且控制效率较高。

3 结束语

以半导体激光器为研究对象，设计一种基于参数辨识的半导体激光器温度自动控制方法。为验证本文方法的温度控制效果，设定高于、低于环境温度2种实验方案，通过半导体激光器的温度波动范围分析其控制效果，通过测试半导体激光器的发光光谱并与文献[4]、文献[5]方法对比，验证其温度控制的有效性。实验结果表明，本文方法可使半导体激光器温度达到预期值，且能快速实现控制，温度波动范围在0.02 ℃内，控制效果更好。