基于自适应滑模控制器的机械臂运动控制方法

2022-12-01丛成

机械与电子 2022年11期

丛成

(中国石油集团川庆钻探工程有限公司长庆钻井总公司，陕西西安 710018)

0 引言

机械臂具有较多特点，如模型不确定、时变和强耦合等，属于非线性系统[1]。机械臂分支中存在负载，当机械臂的加速度、速度和位姿不同时，会发生非线性变化，且各关节在机械臂系统中产生的摩擦力也会出现变化[2]。各通道之间的相互控制、通道输出以及负载系统之间的连接，都会导致机械臂系统出现复杂耦合。上述问题给机械臂运动控制带来了不确定性，因此，需要对机械臂运动控制方法进行分析和研究。

屈海军等[3]提出基于二型模糊遗传控制器的冗余自由度机械臂运动控制方法，但该方法无法消除机械臂运动过程中存在的高频振动，降低了方法的跟踪精度和控制稳定性；王俊等[4]提出基于关节极限的冗余机械臂混沌动力学及控制方法，该方法在控制过程中受高频振动的影响，导致其存在控制性能差的问题。

针对上述问题，提出一种基于自适应滑膜控制器的机械臂运动控制方法。

1 观测器设计

外部干扰信号g通常存在于机械臂控制系统中，如果此时直接对机械臂进行运动控制，会增加机械臂系统的输出。对机械臂运动控制器进行设计时，通过观测器观测能够观测到的干扰信号，其次采用滑膜控制方法[5-6]对无法观测到的干扰信号进行补偿处理。

机械臂系统的动力学方程为

(1)

在上述机械臂系统动力学方程[7]的基础上设计非线性干扰观测器，即

(2)

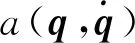
(3)

Q(q)为正定惯性矩阵。

非线性观测器[8-9]在运行过程中的观测误差F表达式为

F=g-

(4)

(5)

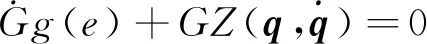
(6)

2 自适应滑膜控制器

基于自适应滑膜控制器的机械臂运动控制方法，通过设计自适应滑膜控制器，完成机械臂的运动控制。

用x1表示机械臂系统的控制误差向量，其计算式为

x1=q-wc

(7)

wc为期望的关节位置矢量。

用B1表示机械臂子系统1的Lyapunov函数[10-11]，其表达式为

(8)

对Lyapunov函数求导，并结合上述公式获得

(9)

(10)

dTd为关节位置滑膜控制误差矩阵。结合上述公式，获得

(11)

扰动ψ在实际过程中是无法直接计算得到的，因此，基于自适应滑膜控制器的机械臂运动控制方法采用自适应率对扰动ψ进行估计。

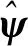
用B表示自适应滑膜控制器的Lyapunov函数，其表达式为

(12)

χ为大于零的常数。根据Lyapunov函数设计自适应滑膜控制器的等效控制律为[12-13]

(13)

F(q)为机械臂动力学模型的标称值；j为正定对角系数矩阵。在此基础上获得自适应滑膜控制器的切换控制律为

υs=-σF(q)jsign(s)

(14)

sign(·)为符号函数；σ为正常数。

(15)

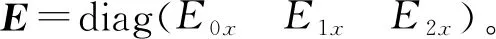
此时将自适应滑膜控制器的切换控制律转变为

(16)

tanh(·)为双曲正切函数，其表达式为

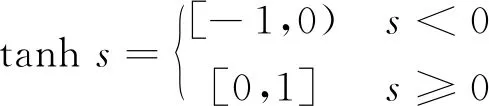
(17)

此时自适应滑膜控制器的总控制律为υ，即

υ=υs+υe

(18)

采用自适应滑膜控制器根据总控制律υ对机械臂进行运动控制。

3 实验与分析

为了验证本文方法的整体有效性，需要对其进行测试。

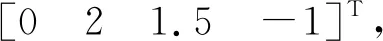
表1 机械臂参数

分别采用本文方法、文献[3]方法和文献[4]方法进行机械臂运动控制测试，跟踪机械臂的运动角度，跟踪结果如图1所示。

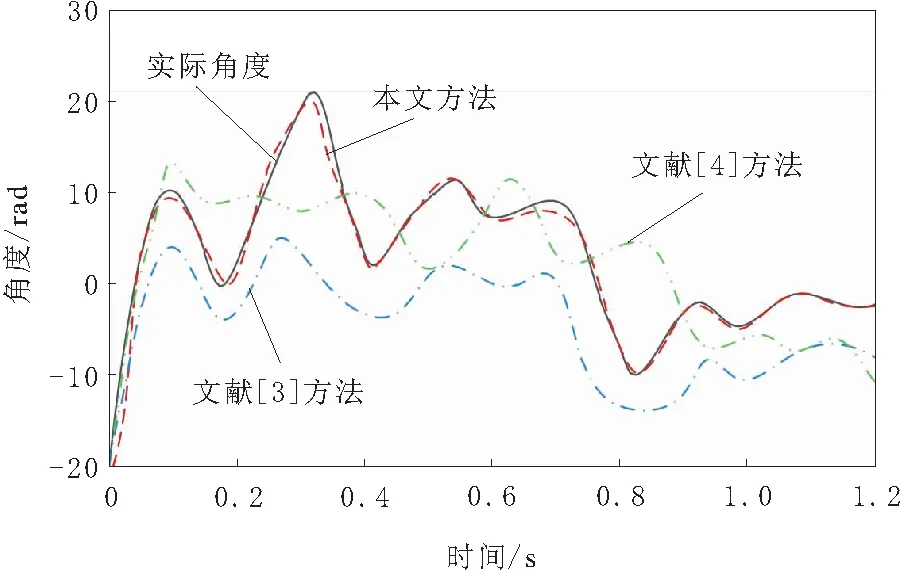
图1 角度跟踪结果

分析图1可知，采用本文方法对机械臂进行运动控制时，获得的移动角度跟踪结果与机械臂实际移动角度基本相符；采用文献[3]方法对机械臂进行运动控制时，获得的角度曲线变化趋势与实际角度变化趋势基本一致，但在相同时间点下获得的角度值均低于实际角度值；采用文献[4]方法对机械臂进行运动控制时，获得的跟踪结果变化趋势和数值都与实际角度存在较大差距。通过上述分析可知，在机械臂运动控制过程中，本文方法可准确跟踪机械臂的移动角度，表明本文方法具有较高的跟踪精度。

在外界干扰τ=[-sint3cost-2sintsint]T测试环境下，通过控制力矩对比不同方法的控制稳定性，测试结果如图2～图5所示。

分析图2～图5可知，在不同的外界干扰环境下，本文方法的控制力矩均没有明显波动，控制力矩随时间变化较为平稳。采用文献[3]方法和文献[4]方法进行控制稳定性测试时，2种方法在外界干扰环境下的控制力存在明显波动，因为文献[3]方法和文献[4]方法无法在机械臂运动控制过程中消除高频振动，导致力矩控制结果的波动较大。而本文方法在设计自适应滑膜控制器的过程中，为了抑制机械臂运动控制过程中存在的高频振动，采用了补偿器，能够有效消除机械臂运动过程中存在的高频振动，进而获得平稳的控制力矩曲线，提高自适应滑膜控制器的稳定性。

图2 τ=-sin t时的控制力矩

图3 τ=3cos t时的控制力矩

图4 τ=-2sin t时的控制力矩

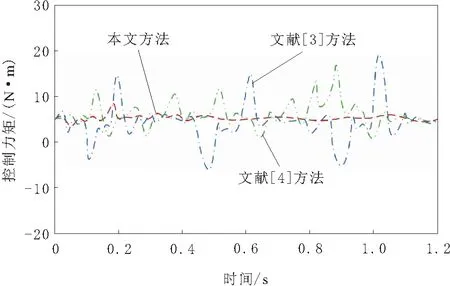
图5 τ=sin t时的控制力矩

根据给定的机械臂轨迹θLd=2cost、θLd=2sint、θ1d=sin 2t、θ2d=cos 2t，采用本文方法、文献[3]方法和文献[4]方法对机械臂进行运动控制，对比不同方法的控制误差，测试结果如图6所示。

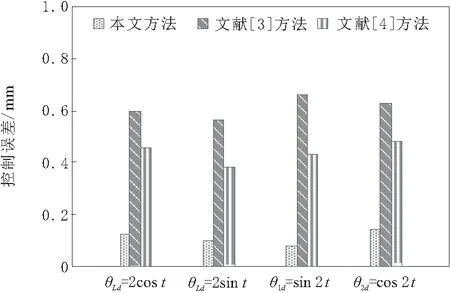
图6 不同方法的控制误差

分析图6可知，采用本文方法对机械臂进行运动控制时，获得的控制误差均保持在0.2 mm以内；采用文献[3]方法进行运动控制测试时，获得的控制误差在0.6 mm上下波动；采用文献[4]方法进行运动控制测试时，控制误差在0.4 mm附近取值。根据控制误差对本文方法、文献[3]方法和文献[4]方法的控制性能进行排序：本文方法>文献[4]方法>文献[3]方法。