噪声中GHZ态和W态混合态的相干鲁棒性研究

周伟峰，徐 淼，陈小余

(1.浙江工商大学信息与电子工程学院，浙江 杭州 310018；2.浙江大学城市学院信息与电气工程学院，浙江 杭州 310015)

0 引 言

将经典信息学与量子力学相结合的量子信息学是近年来最具发展前景的交叉学科之一，其中的量子纠缠和量子相干性都是非常重要的物理资源[1-2]。作为一种资源，相干性理论是用于定量区分经典物理和量子物理的新方法，能更好地理解两者之间的边界。如果相干资源理论局限于最大相干态，则相干资源理论与纠缠资源理论具有许多相似之处[3]。文献[4]提出相干性度量的公理化要求，分别给出基于相对熵和基于l1-范数的相干性度量方法。文献[5]指出两体可分离系统中的量子相干性可以包含在局部或子系统之间的相关性中，并且证明了纠缠是一种特殊形式的相干性。文献[6]将相干性的鲁棒性重构为任何量子态的相干见证算符的期望值，证明了单量子态、所有X-态和所有纯态的相干鲁棒性都和l1-范数相干度量结果一致，但对混合态的相干鲁棒性没有明确的结果。在文献[6]的基础上，本文运用泡利矩阵重构噪声GHZ-W态的密度矩阵，确定特性系数和相干见证算符，并采用最优相干见证者模型对混合态进行分析，得到噪声GHZ-W态的相干鲁棒性。

1 相干鲁棒性

对于一个给定的d维希尔伯特空间，{|i〉}i=1,…,d表示它的参考正交基。如果一个量子态δ的密度矩阵是主对角线形式，则称之为非相干态，即：

(1)

式中，δi为概率分布。对于一个给定的量子态ρ，它的相干鲁棒性定义为[6-7]：

(2)

(3)

(4)

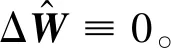
(5)

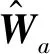
2 三量子比特噪声GHZ-W态

三量子比特噪声GHZ-W态的密度矩阵如下[8]：

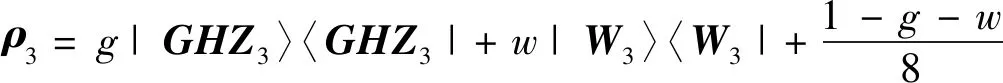
(6)

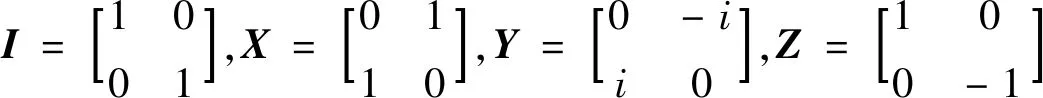
(7)

式(6)中的密度矩阵可以写成不同泡利矩阵的乘积和，

R6(XXI)p+R7(XXZ)p+R8(YYI)p+R9(YYZ)p]

(8)

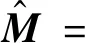
M6(XXI)p+M7(XXZ)p+M8(YYI)p+M9(YYZ)p

(9)

(10)

此时有：

(11)

l1-范数相干度量的定义如下：

(12)

图1 三量子比特噪声GHZ-W态的相干鲁棒性和l1-范数相干度量结果

3 N量子比特噪声GHZ-W态

已知N量子比特GHZ态的态矢量为：

(13)

N量子比特W态的态矢量为：

(14)

式中，|k〉∈{0,1}⊗N为一个二进制向量，|k|为k的汉明重量。那么，N量子比特噪声GHZ-W态的密度矩阵如下：

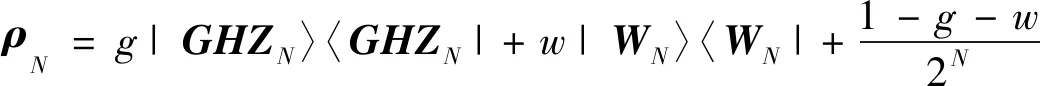
(15)

式中，Ⅱ2N为2N×2N的单位矩阵。将ρN表示为不同泡利矩阵的乘积和形式，

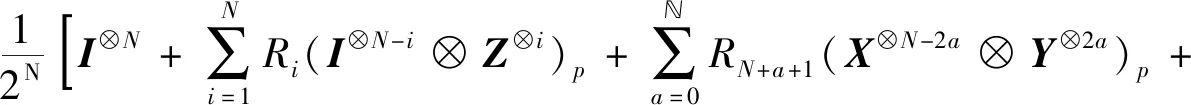
(16)

式中，下标p表示全排列之和，为小于等于N/2的最大正整数，RN+a+1=(-1)ag，RN++1+b=R2N++c=2w/N。记与Rj,j=(1,2,3,…,3N+-1)相乘的泡利矩阵项中的I，X，Y，Z的个数为nI，nX，nY，nZ，与Rj对应的全排列个数记为pj，可以得到：

(17)

R≡(p1R1,p2R2,…,p3N+-1R3N+-1)

(18)

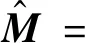
(19)

记M=(M1,M2,…,M3N+-1)。由于{I⊗N-i⊗Z⊗i}均位于主对角线上，因此令对应的m=M1=…=MN=0，所以不必计算{R1,…,RN}的具体值。此时ρN的最优相干见证者为：

(20)

此时有：

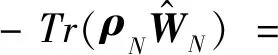
(21)

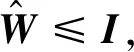
Rc(ρN)=g+(N-1)w

(22)

此时，ρN的l1-范数相干度量结果为：

(23)

所以，任意N量子比特噪声GHZ-W态的相干鲁棒性和l1-范数相干度量的结果一致。

4 结束语

本文研究GHZ态和W态在白噪声中混合态的相干鲁棒性问题。根据混合态的密度矩阵得到特性系数和相干见证算符，构造最优相干见证者，测得相干鲁棒性。但是，本文构建的量子态模型是已知的，无法测量未知混合态的相干鲁棒性，后续将针对任意混合态的相干鲁棒性展开研究。