许可图约束下带释放时间的两机排序算法

童 昕，张 亮,张 安，陈 永，陈光亭

(1.杭州电子科技大学理学院，浙江 杭州 310018；2.浙江水利水电学院信息工程学院，浙江 杭州 310018)

0 引 言

排序最初的应用来源于工业生产，习惯上将可用的资源称之为机器，需要完成的任务称为工件。排序主要研究如何有效利用资源，在限定条件下完成若干任务，使收益最大化。带冲突约束的排序问题起源于资源受限，假设每个工件在加工过程中对某些资源有特定需求，而资源总量有限，当一些工件对某种资源的总需求超过供应时，就会发生冲突[1]。冲突关系可以用一般图来刻画，称为冲突图，图中边的2个端点对应加工窗口不能重叠的2个工件。冲突图的补图称为许可图，许可图中边的2个端点对应加工窗口可以重叠的2个工件。因此，冲突图约束的排序与对应许可图约束的排序是等价的。对于最小化时间表长即最小化最大完工时间的平行机排序问题，Baker等[2]证明了当机器数m≥3时，单位工件的情形是强NP-难的。对于m=2，单位工件的情形等价于在许可图中寻找最大基数匹配问题，因此是多项式时间可解的；对于工件的加工时间pj∈{1,2}的情形，Even等[1]提出一种基于最大匹配的多项式时间最优算法。

对于工件具有释放时间的排序，Bendraouche等[3]证明了以下特殊情形已经是强NP-难的：许可图为二部图G=(N1∪N2,E)，且N1中只含有加工时间为2释放时间为0的工件，N2含有加工时间为1释放时间为0和加工时间为2释放时间为r的工件；他们[4]还将这一强NP-难结论从二部图推广至一类更广泛的许可图情形，即当N1是一个独立集、N2的诱导子图是完全图、二部图等结构的情形。

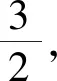
1 问题描述

定义[5]给定图G=(V,E)，若边集M⊆E中任意2条边在G中均不相邻，则称M为G的1个匹配。对于赋权图，定义匹配M的权为M中所有边的权之和。赋权图G的所有匹配中，权最大的匹配称为最大权匹配。

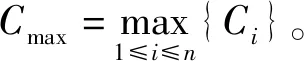
2 算法设计与分析

针对P2|G=(N1∪N2,E),N1={20},N2={10,2r}|Cmax问题，本文设计了一种基于最大权匹配的近似算法。首先，对二部图G中的边进行赋权，任意边e=(Js,Jt)∈E，边的权重me=min{ps,pt}；然后，调用文献[6]提出的KM算法，找到G的最大权匹配M，M中含有(20,10)和(20,2r)这2种边；最后，先加工匹配M中的边(20,10)对应的顶点工件以及孤立工件20和10，保证匹配边对应的工件以及2类孤立工件，两两之间无重叠。若加工完这些工件未到r时刻，则匹配M中的边(20,2r)以及剩余孤立工件2r从r时刻开始无空闲加工；若加工完这些工件达到或超过r时刻，则接着加工匹配M中的边(20,2r)以及剩余孤立工件2r。算法产生的排序分为5种结构，如图1所示。其中结构a表示1个20工件和1个10工件在2台机器上同时进行加工；结构c表示1个20工件在1台机器上单独加工；结构d表示1个10工件在1台机器上单独加工；结构e表示1个20工件和1个2r工件在2台机器上同时进行加工；结构f表示1个2r工件在1台机器上单独加工。在不引起歧义时，a,c,d,e,f也表示各个结构的数量，记算法所产生排序的最大完工时间为Cmax。

图1 算法产生的排序的5种结构

根据最优排序中是否存长链结构，分为以下2种情形。

情形1当不存在长链时，最优排序的结构有6种，如图2所示。结构a*表示1个20工件和1个10工件在2台机器上同时进行加工；结构b*表示1个20工件和2个10工件在2台机器上同时进行加工；结构c*表示1个20工件在1台机器上单独加工；结构d*表示1个10工件在1台机器上单独加工；结构e*表示1个20工件和1个2r工件在2台机器上同时进行加工；结构f*表示1个2r工件在1台机器上单独加工。

图2 无长链时，最优排序的6种结构

从图2可以看出，算法所产生排序的最大完工时间

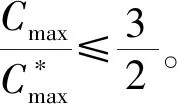
证明算法产生的排序与最优排序中20,2r,10这3种工件的数目相同，则有：

a+c+e=a*+b*+c*+e*

(1)

e+f=e*+f*

(2)

a+d=a*+2b*+d*

(3)

将式(1)×2+式(2)×2+式(3)，可得：

3a+2c+d+4e+2f=3a*+4b*+2c*+d*+4e*+2f*

(4)

算法产生的排序中匹配的权重为a+2e，此情形下最优排序匹配的权重为a*+b*+2e*，则有：

a+2e≥a*+b*+2e*

(5)

由式(4)和式(5)，可得：

证毕。

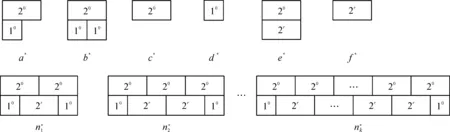
图3 最优排序有长链时的(k+6)种结构

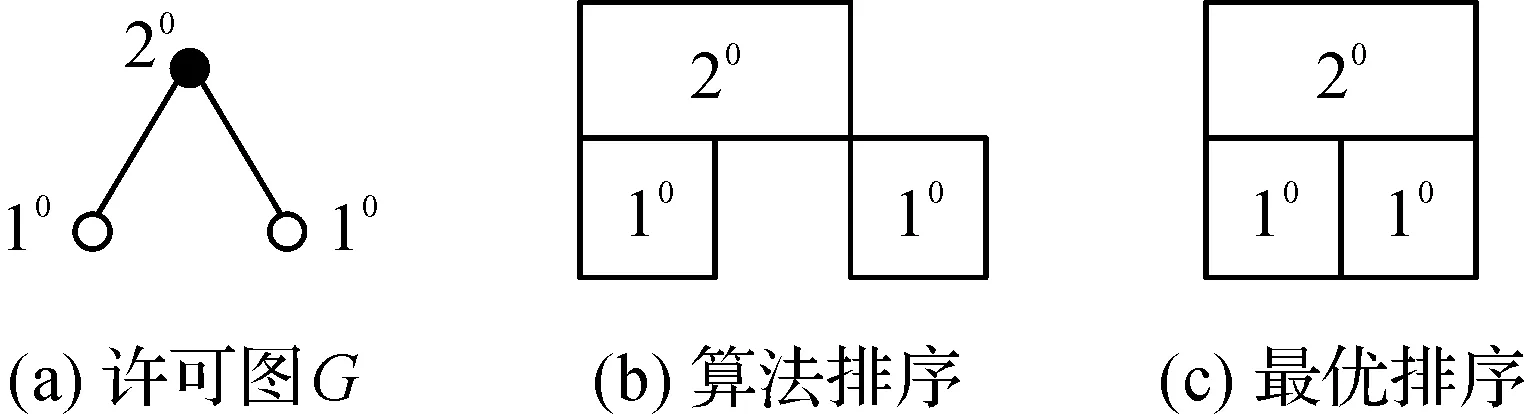
引理2当最优解结构满足情形2时，若进一步有2(a*+b*+c*)+d*

证明用反证法证明。假设最优排序中所有长链都在r时刻之后开始加工，由2(a*+b*+c*)+d*

引理3当最优解结构符合情形2时，必有2(a*+b*+c*)+d*≥r-2。

证明用反证法证明。假设2(a*+b*+c*)+d*≤r-3，按图4对最优排序进行调整，从中可以看出，长链结构使得最大完工时间减少了1个单位时间，这与最优排序矛盾。证毕。

图4 最优排序调整过程

图5 最优排序再次调整过程

情形2中，若最优排序的结构满足2(a*+b*+c*)+d*≥r-1，引理4显然成立。证毕。

证明算法产生的排序与最优排序中20,2r,10这3种工件的数目相同，则有：

(6)

(7)

(8)

由式(6)×2+(7)×2+(8)可得：

(9)

(10)

由式(9)和式(10)，可得：

证毕。

由引理1和引理5得出如下结论。

通过1个例子来验证算法的界是紧的。假设工件集N={20,10,10}，许可图G和算法得到的排序以及最优排序如图6所示。

图6 紧例的许可图、算法排序及最优排序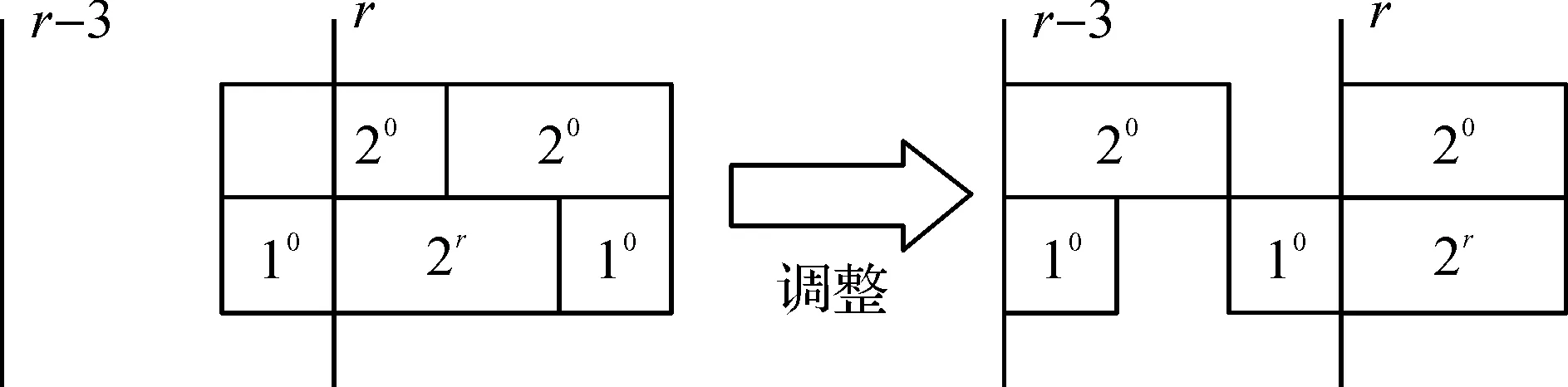

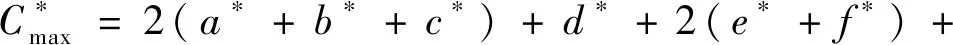
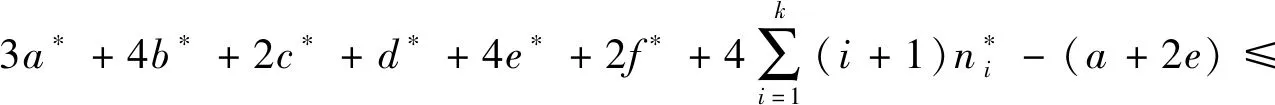
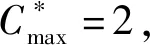
3 结束语