基于LSPIA的带能量项B样条曲线拟合
2022-12-01邓重阳李亚娟
王 越,邓重阳,李亚娟
(杭州电子科技大学理学院,浙江 杭州 310018)
0 引 言
在计算机辅助几何设计的逆向工程及模型设计中,用曲线拟合离散数据有着广泛的应用。B样条曲线具有几何不变性、分段光滑和局部支撑等优点,通常用于曲线拟合[1]。最小二乘拟合是B样条曲线拟合的经典方法,能将拟合误差控制在整体最小[2],但未考虑拟合曲线的能量。因此,在最小二乘拟合基础上添加能量项,以获得能量更小的B样条拟合曲线。传统的带能量项B样条曲线拟合通常是将B样条曲线控制点看作未知量,通过求解线性方程组得到此控制点。渐进迭代逼近是一种高效直观的数据拟合方法,通过迭代调整控制点的位置,获得一系列拟合曲线[3],避免求解一个大型线性方程组。1975年,齐东旭等[4]首次提出PIA的概念,并用于均匀B样条曲线的插值运算,随后被用于各种曲线曲面的插值运算,包括非均匀B样条曲线曲面[5]、NURBS曲线曲面[6]、基于标准全正基函数的混合曲线曲面[7]、Loop细分曲面[8]、Catmull-Clark细分曲面[9]等,后期被推广到曲线曲面的拟合,比如,Lin等[10]提出一种扩展的渐进迭代逼近(Extended Progressive and Iterative Approximation,EPIA)算法,允许控制点的数量小于给定数据点,在大规模数据拟合方面具有重大影响。2014年,Deng等[11]提出一种最小二乘渐进迭代逼近(Least Squares Progressive Iterative Approximation,LSPIA),从上一轮迭代开始新一轮的迭代,节省了大量计算量。2018年,Lin等[12]论证了奇异迭代矩阵LSPIA算法的收敛性。王慧等[13]提出一种B样条曲线的双层最小二乘渐进迭代逼近算法,与LSPIA相比,在减少迭代时间的同时,降低了迭代次数,提高了拟合效率。本文提出一种基于LSPIA的带能量项B样条曲线拟合算法,通过调整能量系数,使得拟合曲线既满足拟合误差精度又能达到能量最小。
1 曲线拟合算法
1.1 带能量项的B样条曲线拟合
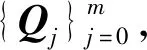
(1)
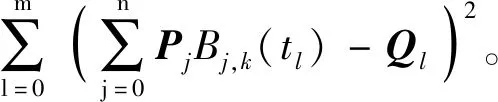
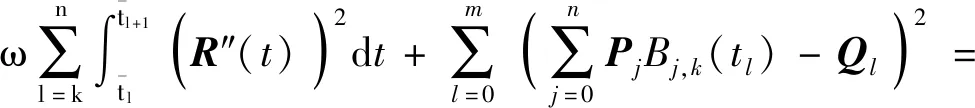
(2)
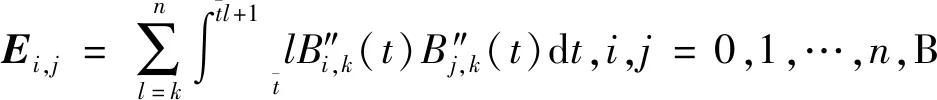
(3)
则可将式(2)表示为矩阵形式:
F=ωPTEP+(BTP-Q)2
(4)
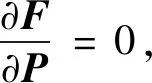
(BTB+ωE)P=BTQ
(5)
式中,Q为给定的数据点集,P为待求的带能量项后B样条曲线的控制点集,ω为能量系数,一般可采用反解法求得P。
由能量矩阵E及B样条基函数的配置矩阵B的定义可知,方程组(5)的系数矩阵为稀疏矩阵,用反解法导致系统不稳定,且消耗大量计算资源,渐进迭代逼近方法可以解决这个问题。
1.2 带能量最小二乘渐进迭代逼近
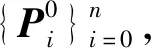
(6)
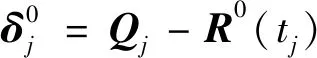
(7)
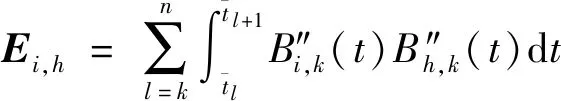
(8)
(9)
则第r+1次迭代后的控制顶点为:
(10)
将上述迭代过程写成矩阵形式,可得:
(11)
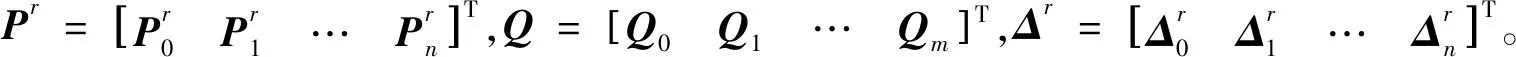
1.3 收敛性证明
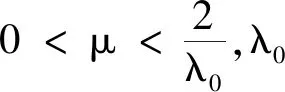
证明令In+1为n+1阶单位矩阵,由式(11)可知,Pk+1=Pk+μ(BTQ-VPk),则有:
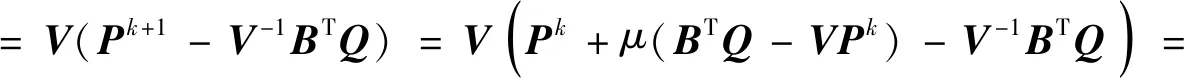
V(I-μV)(Pk-V-1BTQ)=…=V(I-μV)k(P0-V-1BTQ)
(12)
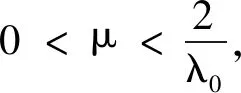
1.4 优化能量系数
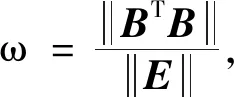
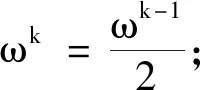
1.5 基于LSPIA的带能量项B样条曲线拟合算法
根据1.2节提出的带能量最小二乘渐进迭代逼近,本文提出的基于LSPIA的带能量项B样条曲线拟合算法(简称带能量LSPIA算法)主要运用1.4节的二分法对能量系数进行调整,在满足拟合误差精度的条件下,使得B样条曲线能量最小,并具有较好的鲁棒性。算法流程如下。

输入:数据点{Qj}mj=0,初始控制顶点{P0i}ni=0,精度ε1,ε2。(1)给定控制点数,运用LSPIA得到满足拟合误差精度ε1的B样条曲线,若在给定控制点下无法达到拟合误差精度,增加控制点数。(2)令ω=BTBE,将步骤1得到的B样条曲线作为初始拟合曲线,运用式(11)计算,当迭代中Δl2<ε2时,输出此能量系数对应的拟合曲线。(3)将步骤2输出的B样条曲线的拟合误差记为ε(ω),与精度ε1进行比较。(4)运用式(11)得到调整ω的B样条曲线,用1.4节二分法调整ω,找到1个ω,使得f(ω)=ε(ω)-ε1=0,得到尽可能大的能量系数和最终的拟合曲线。输出:控制顶点{Pi}ni=0。
2 实验结果与分析
实验平台的操作系统为Windows 10,测试工具为MATLAB R2017b。运用MATLAB提取一些图像模型的边缘轮廓,获得9个测试数据集。在计算机辅助几何造型技术中,三次B样条曲线的应用广泛,故本文采用三次B样条曲线进行实验。分别使用LSPIA算法和本文提出的带能量LSPIA算法进行拟合,得到相同拟合误差精度下的拟合曲线能量如表1所示。
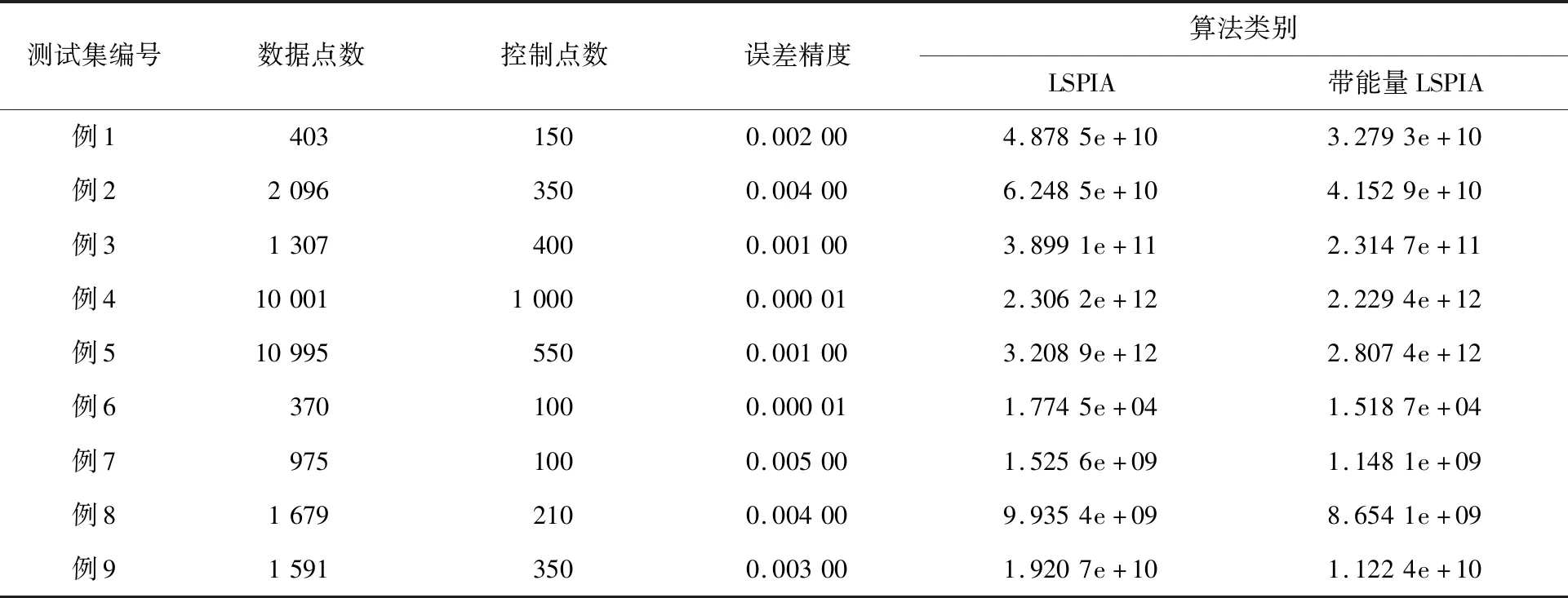
表1 相同拟合误差精度下,2种算法的曲线能量
由表1可以看出,相同拟合误差精度下,采用带能量LSPIA算法得到的拟合曲线比LSPIA算法得到的拟合曲线的能量小。曲线能量越小,曲线越光滑,曲线质量越高。
图1展示了用LSPIA算法和带能量LSPIA算法拟合表1中例1—例3数据的拟合效果及其局部放大图,箭头下方为对应的局部放大图,实心点为数据点。
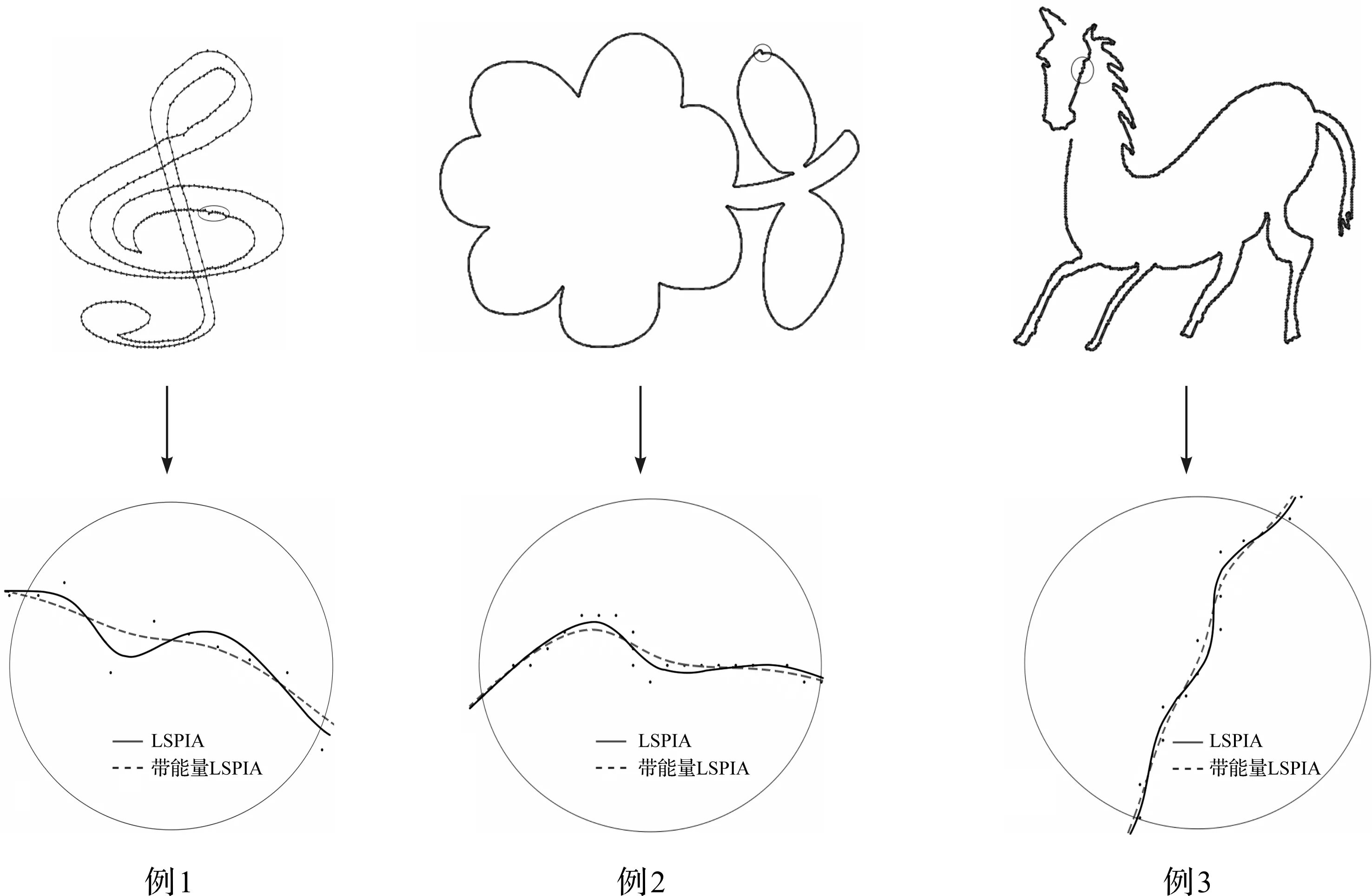
图1 2种算法的部分拟合结果
从图1可以看出,2种算法均能满足拟合误差精度,数据采样点均匀处都有比较好的拟合数据点。但从局部放大图看,在采样点不均匀处,本文算法得到的拟合曲线更光滑,曲线质量更高。
采用2种算法拟合例1—例3曲线的曲率如图2所示。
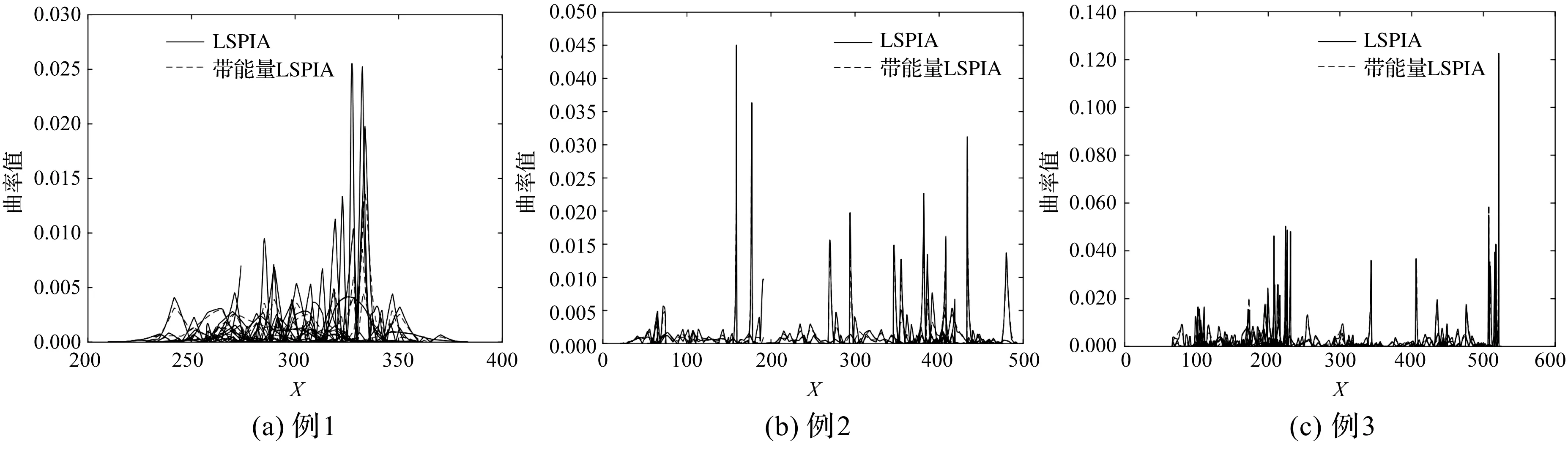
图2 2种算法拟合例1—例3曲线的曲率
从图2可以看出,本文提出的带能量LSPIA算法得到的曲线曲率更小,拟合曲线更光滑。
例4、例5图中含有大规模离散数据点集,用带能量LSPIA算法拟合的效果如图3所示。

图3 运用带能量LSPIA拟合大规模数据点集的拟合结果
从图3可以看出,带能量LSPIA算法可以有效拟合数据量较大的离散数据。当数据点数量比较多时,反解法使得系统不稳定。带能量LSPIA算法是迭代算法,相比反解法,具有更好的鲁棒性。
图4展示了用带能量LSPIA算法拟合例6—例9的拟合效果,其中实心点为原始数据点,箭头下方为三次B样条曲线的最终拟合效果。
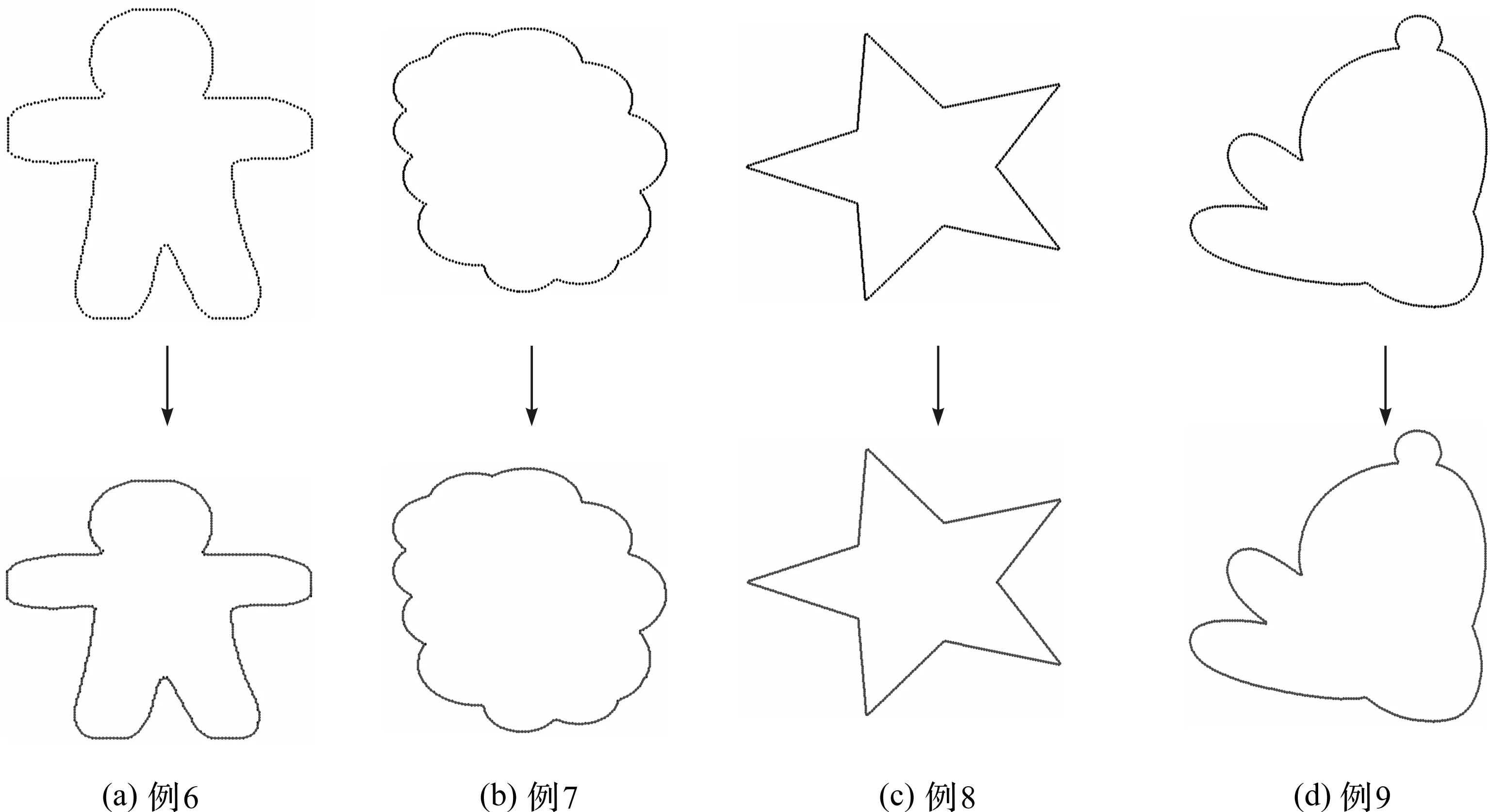
图4 带能量LSPIA用于其他曲线例子的拟合结果
从图4可以看出,采用带能量LSPIA算法均获得较好的拟合效果。
3 结束语
在LSPIA基础上,本文将能量应用于B样条曲线拟合,提出一种带能量LSPIA算法,得到更小的拟合曲线能量。本文采用的是迭代算法,与反解法相比,稳定性更强。后续计划运用本文提出的带能量LSPIA算法对曲面拟合展开进一步研究。
