二分量KN系统三阶流方程的达布变换及其解

周华鑫，虞 静

(杭州电子科技大学理学院，浙江 杭州 310018)

0 引 言

二分量Kaup-Newell(KN)系统是一个非常重要的可积系统，由Kaup和Newell提出[1]，在数学、物理、化学、生物、通信、天体等自然领域均有广泛应用。达布变换是构造可积方程解的最有效方法之一，关于KN的达布变换的研究有很多，如NLS方程达布变换的构造[2]、通过达布变换求怪波解[3-4]、DNLS方程达布变换的行列式表示[5]、部分高阶解的行列式表示[6]等，运用达布变换可得到TOFKN方程的孤子解、positon解、呼吸子解和怪波解[7]，但大多数集中在单分量KN的情形，关于二分量KN系统的研究较少，如二分量DNLS方程[8]、二分量二阶流方程的达布变换的构造[9]、二分量二阶流方程的怪波解[10]等。本文主要研究二分量KN系统的三阶流方程的达布变换并求其解。

1 二分量KN系统的三阶流方程的构造

二分量KN系统的谱问题如下：

(1)

式中，

其中，

i是虚数单位，λ是谱参数，q1,q2,r1,r2是位势，Ψ=(f,g,h)T是特征函数。

由谱问题的相容性条件[11]Ψx,t=Ψt,x导出零曲率方程Ut-Vx+[U,V]=0。将U,V代入零曲率方程后得到：

(2)

此为二分量KN系统的三阶流方程。

(3)

式中，“*”表示复共轭。

2 达布变换

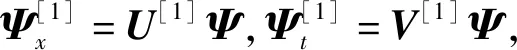
T=T(λ)=Aλ2+Bλ+C

(4)

式中，A=(aij)3×3,B=(bij)3×3,C=(cij)3×3，aij,bij,cij均为关于x,t的函数。通过直接计算不难得到：

U[1]T=Tx+TU

(5)

V[1]T=Tt+TV

(6)

将式(4)代入式(5)，并比较λj(j=4,3,2,1,0)的系数，得到：

(7)

类似地，将式(4)代入式(6)中，并比较λj(j=8,7,6,5,4,3,2,1,0)的系数，得到：

(8)

由式(7)和式(8)可以发现，a12=a13=a21=a31=0，且b11,b22,b23,b32,b33均为常数，C为常数矩阵。为了得到非平凡的解，且要确保其一般性，取b11=b22=b23=b32=b33=0,c12=c13=c21=c23=c31=c32=0,c11=c22=c33=-1。通过以上分析，达布矩阵T的表达式为：

(9)

式中，a11,a22,a23,a32,a33,b12,b13,b21,b31为关于x和t的待定函数。为了确定b12,b13,b21,b31的表达式，记谱问题在特征值λ=λk(k=1,2,3)时对应的特征函数为Ψk=(fk,gk,hk)T。

定理二分量KN系统的三阶流方程(2)的达布矩阵(9)中的元素a11,a22,a23,a32,a33,b12,b13,b21,b31可以用与谱参数λ1,λ2,λ3对应相关的特征函数Ψ1,Ψ2,Ψ3的行列式表示如下：

(10)

式中，

证明运用达布变换的零化条件T(λ)|λ=λjΨj=0(j=1,2,3)，可以推出达布矩阵(9)中元素的行列式表达式(10)。证毕。

在二分量KN系统三阶流方程的达布变换的研究中，发现该方程达布变换的行列式与二分量KN系统二阶流方程达布变换的行列式表示[9]是相通的，说明在求解可积的非线性偏微分方程时，达布变换是一种有效可行的方法。

经过达布变换，通过计算得到二分量三阶流方程(2)的新解为：

(11)

(12)

下面运用上述所得的达布变换(9)及新解的表达式(12)，推导出二分量KN系统三阶流方程的解。在谱问题(1)中，考虑从零种子解出发，即当q1=q2=r1=r2=0时，得到对应的特征函数为：

(13)

代入到解的表达式(12)中，求得二分量KN系统三阶流方程的解为：

(14)

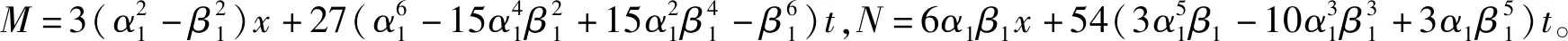
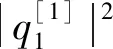
图1 各阶孤子解的三维动力演化图

图2 各阶孤子解的密度图

由图1(a)可以看出，二分量KN系统的三阶流方程的一阶孤子解是一个光滑的孤子解，由图1(b)的二阶孤子解和图1(c)的三阶孤子解的图像可以看出，在x=0,t=0的位置，亮孤子发生局部碰撞，使得波峰轨道产生局部相移，并在x=0,t=0处取得最大振幅。

3 结束语

本文从二分量KN系统的谱问题出发，主要研究二分量KN系统三阶流方程的达布变换和该方程的一些解。在前人研究的基础上，首次研究了三阶流方程的达布变换以及孤子解。研究发现，在求解可积的非线性偏微分方程时，达布变换是一种有效可行的方法。是否能采用行列式的形式来表示二分量KN系统的三阶流方程的n重达布变换，进而求得该方程的其它类型解，是本文后续的研究重点。