组织因素对在役装置安全仪表系统SIL评估影响
2022-12-01杨志华付建民孟晓璇
杨志华,朱 超,付建民,甄 佳,孟晓璇
(1.国家管网集团东部原油储运有限公司,江苏徐州 221000 2.中国石油大学(华东)海洋油气装备与安全技术研究中心,山东青岛 266580)
0 前言
我国石油、化工企业装置向大型化、自动化和工艺复杂化发展,由人引发的如泄漏、火灾、爆炸等事故逐渐增多[1]。安全仪表系统(safety instrument system, SIS) 作为石化企业装置最后一道防火墙在石油化工装置中已经得到了广泛的应用。国际电工委员会颁布的IEC61508《电气/电子/可编程电子安全系统的功能安全》和IEC61511《过程工业领域安全仪表系统的功能安全 第2部分:GB/T 21109.1的应用指南》创建了相应的计算模型以评估SIS可靠性,包括定性、定量和半定量3类[2,3]。设备技术可靠性已提高,由组织错误导致的事故相对有所增加,SIS可靠性降低,从而达不到所需求的安全完整性等级(SIL)。因此,有必要深入研究组织因素对SIL评估影响。目前,国内外学者研究受人因可靠性影响的系统SIL评估,英国心理学家Reason在《人误》一书中最早提出了“组织错误”一词,此外还介绍了贡献因素、潜在失效理论及管理导致事故的概念[4]。Øien[5]基于对现有组织因素框架的回顾,开发出一个组织模型来分析海上设施的泄漏事件。此外,他提出了组织风险指标和量化组织对风险影响的方法。Akbar,等[6]提出了结合FBN和HFACS的方法用于分析过程事故中的人和组织因素。谢彤彤[7]对人的可靠性进行了深入研究,基于THERP+HCR的数学模型,在HRA分析中考虑组织因素,为提高系统可靠性和安全性提供决策建议。刘俊芳[8]基于LOPA分析方法对石化行业定量化人因分析的流程进行研究并提出相应模型,进行其他IPL的有效性计算。池亚娟,等[9]提出了间歇装置受人因影响的SIL评估模型,并提供相关管理措施降低人因失误,从而提高SIL。
目前国内外对于安全仪表系统评估所提出的评估模型较为成熟,且对于人因可靠性分析,目前也有较完整的评估方法,此外虽然针对组织因素下的人因可靠性分析有较多研究,但是在石化企业组织因素对SIS评估的分析量化较少,需进一步研究。基于某液氨储罐装置的现有风险,采取HAZOP结合LOPA的方法进行过程风险分析,并通过分析结果进行SIL确定及验证,构建组织因素影响下的SIL验证模型,评估组织因素对SIL影响水平,提出优化方案从而提高系统SIL。
1 组织因素下的SIL评估
1.1 基于HAZOP和LOPA的风险分析
HAZOP结合LOPA分析方法步骤:①对生产工艺过程进行节点划分,并进行HAZOP分析;②根据HAZOP分析结果,将参数偏差原因作为初始事件,并确定初始事件发生频率;③辨识每个偏差可能的初始原因(每个偏差可能不只一个初始原因);④辨识除SIS外的独立保护层(IPLs),并判定其有效性;⑤根据初始事件发生频率和IPLs失效频率,计算危险事件剩余风险,判断是否需要SIS及其SIL等级。
1.2 组织因素影响下的SIL验证模型
1.2.1 Markov模型
进行合理的SIL等级验证是研究SIF完整性的第二步,但是安全仪表系统在运行阶段易受各种因素影响,如包括系统设计、相关的测试和维护策略、社会技术系统的运行条件。本次SIL验证计算采取Markov模型。 考虑以1oo2冗余结构的危险失效风险为例,构建的Markov模型见图1。1oo2的Markov有6种状态:0-正常;1-降级检测到的;2-降级未检测到的;3-系统安全失效;4-系统危险失效;5-未检测到系统危险失效。
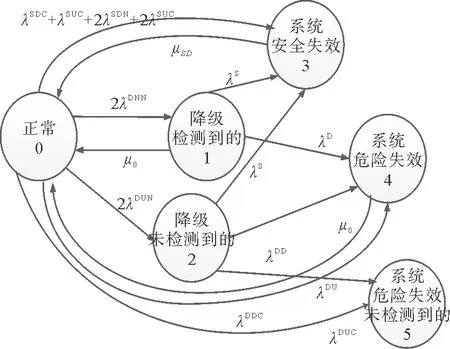
图1 1oo2结构Markov模型
1oo2系统状态转移矩阵P如式(1)所示:

(1)
式中:λS——安全失效率,h-1;
λD——危险失效率,h-1;
λSU——检测到的安全失效率,h-1;
λSD——未检测到的安全失效率,h-1;
λDD——检测到的危险失效率,h-1;
λDU——未检测到的危险失效率,h-1;
λSDC——检测到的共因安全失效率,h-1;
λSUC——未检测到的共因安全失效率,h-1;
λSDN——检测到的非共因安全失效率,h-1;
λSUN——未检测到的非共因安全失效率,h-1;
λDDC——检测到的共因危险失效率,h-1;
λDUC——未检测到的共因危险失效率,h-1;
λDDN——检测到的非共因危险失效率,h-1;
λDUN——未检测到的非共因危险失效率,h-1;
μ0——在线维修率;
μSD——停车维修率。
t时刻需求失效概率:
PFD(t)=[1 0 0 0 0 0]Pt[0 0 0 0 1 1]T
(2)
式中:PFD(t)——t时刻的需求失效概率,h-1;
P——状态转移矩阵;
T——周期性检查时间,h。
1.2.2 奶酪模型
石油化工行业在役装置的安全仪表系统,其成功执行安全功能不仅取决于系统本身结构设计和硬件可靠性,更需要考虑组织因素对其产生的影响。瑞士奶酪模型是著名的组织事故模型,与安全仪表系统的运行阶段高度相关,因此开发了改进的瑞士奶酪模型,如图2所示,该模型考虑了组织因素对操作阶段SIL验证的影响。

图2 改进的瑞士奶酪-组织事故模型
改进的瑞士奶酪模型显示了防御的性能如何受到上游人为因素和组织因素的影响。上部分代表事故因果的主要要素即危害,防御(安全屏障)和损失,下半部分显示了组织事故的发展:组织因素(由组织文化决定的战略决策和一般组织过程)影响当地工作场所条件(时间压力,培训不足,程序不明确等),再加上人类的自然倾向,产生不安全的行为。这些不安全行为可能会在防御中造成漏洞[10]。根据Reason的研究,工作场所和组织因素也可能直接导致防御失败。考虑石油及化工企业实际情况,探究以下8大组织因素,见表1。IEC61508提供了安全仪表系统定量和定性的分析方法,确定系统启动时SIL等级满足情况(设计SIL),由于在系统运行阶段受到人和组织的影响,SIL等级可能发生变化(操作SIL),良好的安全管理对SIL等级提高可能不显著,但是不良的安全管理将恶化系统安全性能,文中仅考虑运行阶段人和组织因素影响,假设设计SIL已考虑相关的人和组织因素影响。考虑组织因素的SIL验证模型,详细分析流程如图3所示。
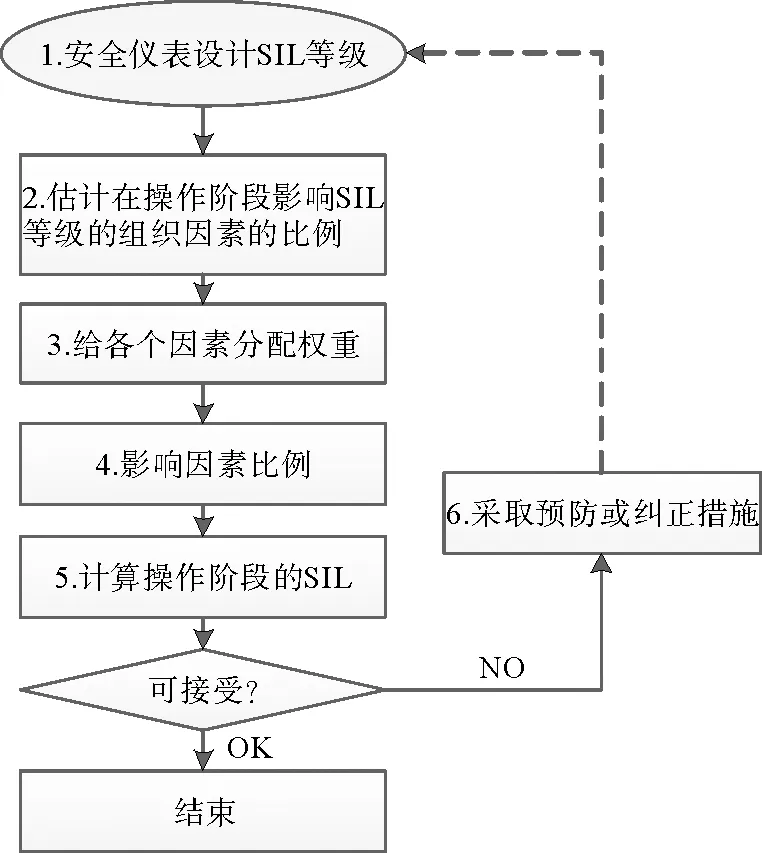
图3 考虑组织因素SIL验证方法流程
1.2.3 安全仪表系统设计SIL的确定
设计的SIL等级采用选定的SIL验证Markov模型,在验证过程中考虑到参数数据时,对于信息充分的设备,SIL验证时可参考数据库。针对厂区缺乏详细数据的设备,为了解决数据的不确定性,引入了Monte Carlo(蒙特卡罗)模拟进行处理[11]。Monte Carlo是一种随机模拟方法,使用随机数进行随机抽样,利用随机抽样值进行计算,确定概率的近似解,文中采取MATLAB GUI进行Monte Carlo模拟,具体的步骤如下:①分析不确定性参数特征,依据历史资料及专家意见,确定参数分布规律;②根据参数分布规律,生成随机数;③建立失效概率(PFD)计算模型,并确定模拟次数n;④依据生成的随机数,重复步骤①、②,计算出n个PFD输出值;⑤根据仿真计算得到的n个PFD的值,利用函数得到均值、标准差、置信区间。
采用高斯误差函数对数据进行处理,得到失效参数数据上下限。以传感器为例将参数λD转换为对数正态分布,其余参数设定为均匀分布,转换步骤见式(3)~(6):
(3)
(4)
μ=lnx0
(5)
(6)
式中:M——失效数据最大值,h-1;
m——失效数据最小值,h-1;
x0——等于T;
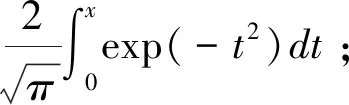
μ——PFD均值;
σ——PFD标准差;
P——置信区间,取值为0.95。
最终得到各参数分布为logN(μ,σ)[12]。
1.2.4 影响安全仪表系统操作SIL等级的组织因素
影响安全仪表系统操作SIL等级的组织因素有8项,具体见表1。

表1 影响安全仪表系统运行阶段的组织因素
1.2.5 由组织因素引起的影响设计SIL的比例θ
组织因素引起的影响设计SIL的比例θ取决于系统设计和操作条件,可以使用专家判断为特定系统估算此比例,如表2所示。

表2 组织因素引起的影响设计SIL的比例θ
1.2.6 计算归一化的权重因子wi
权重wi可以作为安全审核的一部分来确定,使其特定于所考虑的系统,或者可以使用专家判断为整个应用领域(石油、化工、海上等)确定具体的权重。此外,可以从事故因果统计中获得权重见式(7)、(8)。
(7)
(8)

wi——第i种组织因素的权重因子。
1.2.7 评估组织因素Ri
组织因素的等级Ri是通过审核获得的,每个组织因素的等级从0到1,其中0为最佳等级(不需要改进),1为最差等级(需要紧急关注)。这些评级基于针对每个组织因素的一组特定且可测量的指标,最好采用可以用“是”或“否”回答的问题的形式。例如,“同一程序中有时存在多个版本?”,在这种情况下,如果对问题的回答为“是”,则指标会在引起关注的方向上评分,引起关注的指标数量除以用于该安全影响因子的指标总数(假设指标权重相等),从而得出组织因素i的评级Ri。
1.2.8 操作SIL计算
操作SIL的计算见式(9)。
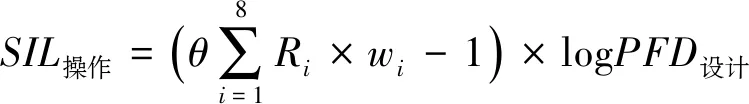
(9)
式中:θ——组织因素影响操作SIL的比例;
Ri——第i个组织因素的等级;
PFD设计——根据设计要求的平均失效概率。
2 组织因素分类与分析
传统的层次分析法使用一个确切的值来表达决策者对备选方案的意见,无法处理不确定性和不精确性的数据,为了克服这些缺点,考虑使用模糊层次分析法(Fuzzy Analytical Hierarchy Process,FAHP)解决层次问题,简化了人们判断目标相对重要性的复杂程度,分析更方便、快捷。采用FAHP对组织因素对安全仪表系统评估影响度进行计算评估,进而对影响SIL的子因素进行重要度排序。
a) 构建分析结构模型:找出各因素之间的隶属关系。
b) 建立模糊判断矩阵:某一层元素中包括的各子元素相对重要度。模糊判断矩阵见公式(10)。
(10)
其中各元素之间的隶属度关系用0.1~0.9标度法表示,如表3所示,所构造的模糊判断矩阵为模糊互补矩阵。

表3 元素两两比较0.1~0.9标度表示法
c) 一致性检验:一致性检验直接影响实际因素之间的客观排序。

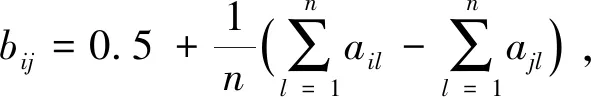


(11)
3 组织因素对SIL评估影响实例研究
以液氨储罐液位高报警为例,分析组织因素对运行阶段仪表系统SIL等级的影响。储罐液位联锁LIAS501C功能:液位变送器LIT501C检测储罐V101液位,当储罐液位超过设定值(≥1 800 mm)时,液位变送器LIT501C将信号传给中控室PLC系统,经处理后将信号传给进料阀LSV101联锁切断。
3.1 组织因素影响度识别
运用模糊层次分析方法分析组织因素对安全仪表系统的影响程度,建立组织因素层次结构模型。
邀请10位专家(人因可靠性分析专家、组织行为学专家、企业管理人员等)参与整个量化分析过程,结合安全仪表系统的特点对指标的量值进行判断,采用0.1~0.9表达重要程度,所得结果如表4所示。
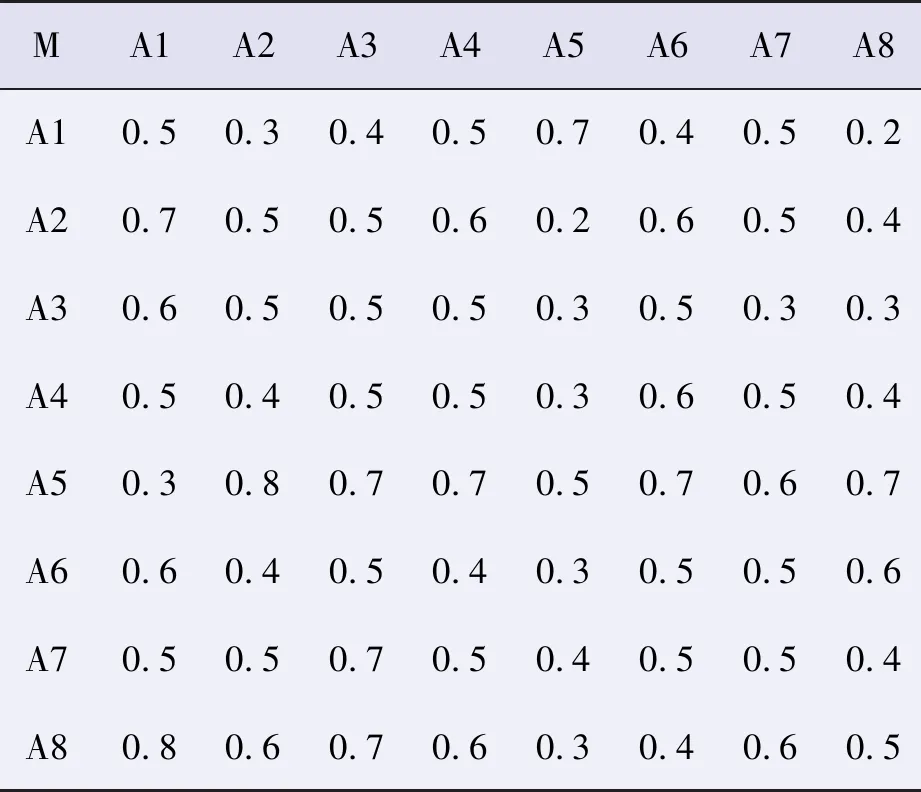
表4 影响运行阶段仪表系统SIL等级的模糊矩阵M
由表4可构建模糊互补矩阵的可达矩阵T,如式(12)所示。

(12)
由可达矩阵T可知对角线上不存在为1的元素,由一致性检验标准可知,矩阵M满足一致性检验,分析小组根据元素之间的重要程度,一致选取α=6作为判断参数,则α=6,n=8,由公式(1)计算可知组织因素A1~A8的相对影响度为:
R1=(0.114 6,0.125 0,0.114 6,0.118 8,0.145 8,0.120 8,0.125 0,0.135 4)
3.2 SIL确定
对整个工艺装置进行HAZOP分析,选取液态烯烃储罐卸料“来量大”偏差进行LOPA分析,分析过程如下。
a) 场景描述:储罐来量大,储罐V101液位高,导致储罐V101高液位冒罐溢流。
b) 事故后果:储罐高液位冒灌溢流,造成人员中毒。
c) 初始事件:卸料来量大,偏差发生可能性0.1。
d) 条件修正:事故场景的发生需要触发事件,需考虑修正因子。①点火概率:p1=1 (不考虑立即点火还是延迟点火);②人员暴露概率:p2=0.1;③致死概率:p3=1。
e)IPLs确定:IPLs可以是设备、系统或一系列对应的行动,用来预防或减轻不希望的后果,这些设备、系统或行动可不受干涉,独立起到保护作用。此场景的IPLs及其PFD(需求时失效概率)如下:关键报警及人员响应:液位超高时,人员不能及时作出有效响应,故不作为IPL。
式(13)为后果发生频率F确定:

(13)
式中:p0——初始事件发生概率;
pi——第i个修正因子发生频率;
PFDj——第j个保护层的需求失效概率。
f) 现有风险等级:事故后果严重程度为D,发生频率为4×10-4,参考中国石化风险评估矩阵确定现有风险为中风险。
g) 残余风险:由以上分析可知,风险确定为“中”,建议降低风险为“低”,故残余风险PFD=0.1~0.01。
h) 风险决策(SIL需求):液氨储罐V101液位联锁控制SIL需求为SIL1。
3.3 SIL验证
首先根据提出的分析模型确定设计的SIL等级,相关数据参考国外通用的OREDA和PDS数据库,建立Markov模型计算设计SIL等级,基本的可靠性数据如表5所示,计算结果如表6所示。
然后对储罐V101安全仪表系统可靠性数据进行Monte Carlo模拟,详细的数据分布如表7所示,MC-Markov计算结果如表8所示。
由表8可知,采用Monte Carlo模拟系统95%置信区间PFDavg值为2.45×10-2,系统为SIL1。在实际工程中,直接采用数据库的数据或采用上下限值进行计算可能存在较大误差,使得计算结果过于乐观,不能保证风险合理降低,采用Monte Carlo模拟可弥补数据缺失的情况,同时给出95%置信区间PFDavg值,使得计算结果更科学。

表5 系统可靠性数据

表6 Markov SIL计算结果
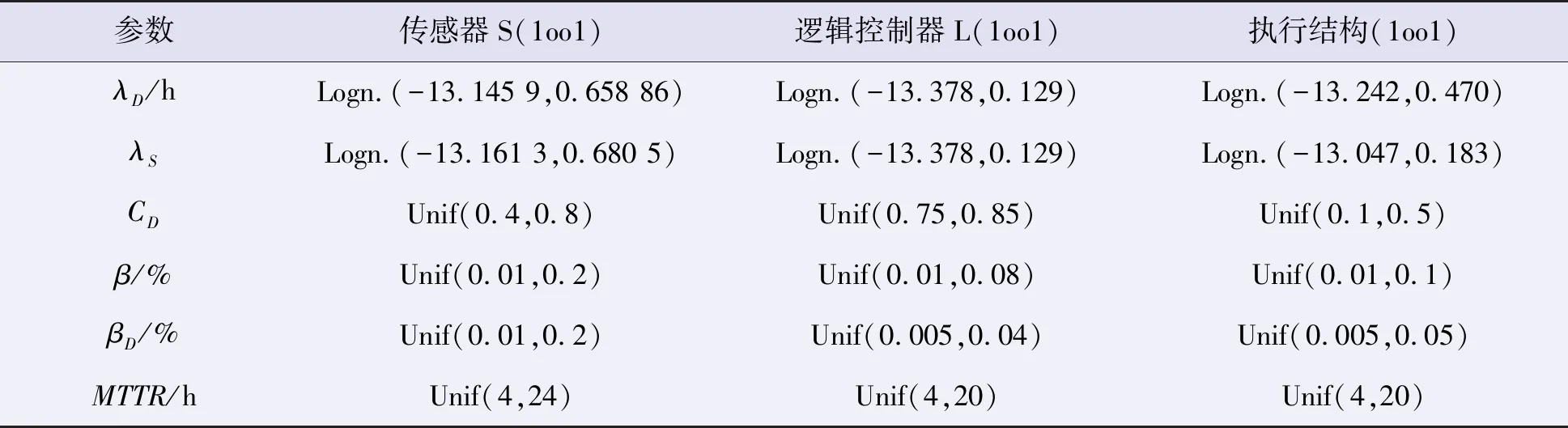
表7 液氨储罐V101安全仪表系统可靠性数据分布

表8 MC仿真计算Markov模型结果
由以上计算可知,设计PFDavg为2.45×10-2,SIL等级为SIL1,影响安全仪表系统运行阶段SIL等级的组织因素,如表1所示。估计由人和组织因素引起的影响设计SIL的比例θ,如表2,假设人和组织因素对设计SIL影响较敏感,θ取值为0.7;影响安全仪表系统组织因素分配权重并计算归一化的权重因子wi;在对影响安全仪表系统组织因素分配权重的问题上,分两种情况讨论:①以组织因素影响度识别为基础,量化计算得到的权重进行计算;②假设组织因素的权重均为0.125,这些因素对安全仪表系统影响同等重要。
评估安全影响因素Ri:Ri是从审核中获得的,其中包含针对每个组织因素的一组特定的、可测量的指标。Ri的最低值、最高值和平均值评级如表9所示,该结果来自ARAMIS案例研究。
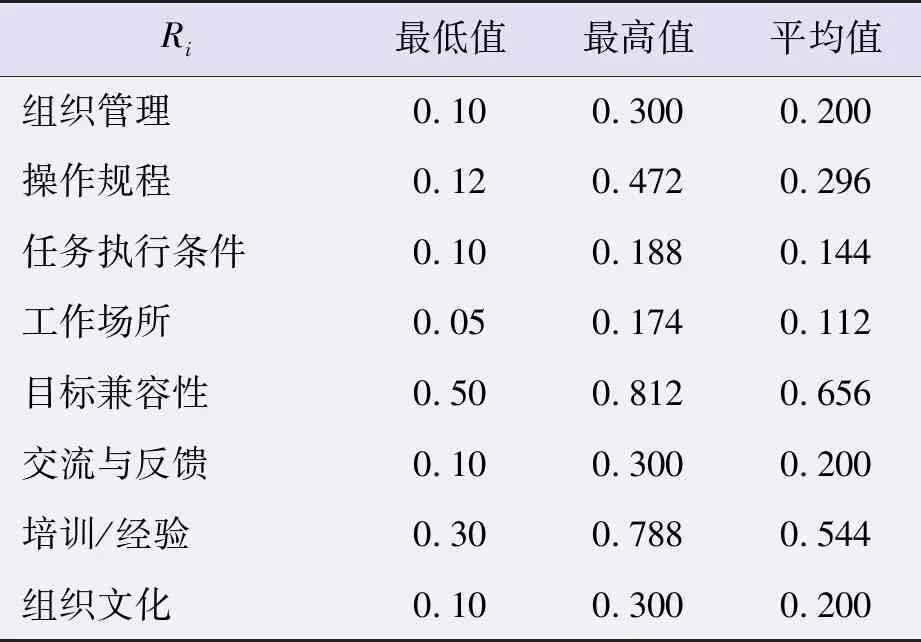
表9 评估安全影响因素Ri
经计算可得,每个组织因素权重不相等时,SIL操作为1.29,每个组织因素权重相等时,SIL操作为1.31。
设计SIL与操作SIL计算结果见表10,案例不同θ值对操作SIL及RRF的影响见表11。

表10 设计SIL与操作SIL计算结果

表11 案例不同θ值对操作SIL及RRF的影响
对于确定权重值和Ri下,θ值对SIL等级无影响,但是当人和组织因素对安全仪表系统逐渐敏感时,RRF值逐渐增大,可能达到临界值,操作SIL改变,而使得设计SIL不满足,导致需进行新的设计,见图4。因此,应重点考虑操作阶段人和组织因素对安全仪表系统的影响。

图4 案例研究中设计和操作SIL
图5为组织因素的加权等级。由表11和图5可知,尽管此时的操作SIL等于设计SIL,但是对应的PFD值不同,即组织因素影响对操作SIL产生影响,此外,两种组织因素权重值情况下,操作SIL不同,因此在操作SIL低于1之前,应采取预防措施。从图5可以看出,目标兼容性(红色)和培训(黄色)具有最高的权重评级,并且最需要改进。然后,将来自审核的信息用作深入分析这些安全影响因素的起点,以找出不良评级的原因。这样,可以采取预防措施来改善相应组织因素。例如,管理层可以对不兼容的工作组进行干预,并对操作人员使用警报系统进行培训。当目标兼容性和培训得到改善后,应该重新评级并计算新的操作SIL。

图5 组织因素的加权等级
提出的计算模型可以用作较大的SIL监控策略的一部分,以便在安全仪表系统的操作阶段将SIL保持在所需水平。需要进行进一步的研究,以探讨在运营阶段其他问题,包括系统修改的影响和设备的老化,并评估它们对运行SIL的影响。
4 结论
a) 依据IEC61508和IEC61511要求的功能安全标准,对液氨储罐装置使用HAZOP结合LOPA的方法进行风险分析,确定了液氨储罐所需降低风险量。
b) 对影响安全仪表系统的组织因素进行了定义和分类,对组织因素进行了影响度识别,构造因素相对影响度、总体影响度以及重要度3个指标,计算出各个指标的相对影响度,并对重要度进行了排序,经过评估得出目标兼容性、培训/经验对安全仪表系统影响较大。
c) 在进行SIL确定时,考虑组织因素影响,对LOPA保护层中“关键报警及人员响应—人因保护层”进行分析确定,采用了层次任务分析法和奶酪模型方法确定“人因保护层”能否作为独立的保护层,并最终对SIL进行确定,并将这一方法应用至液氨储罐高液位场景。结果表明,相对于传统的SIL确定模型,提出的模型可以较好地对“人因保护层”进行分析,从而对SIL确定得到更准确的分析结果,为实际提供指导。
d) 在进行SIL 验证时,IEC61511提供了安全仪表系统设计和实施的一般框架,但对安全仪表系统操作受人和组织因素影响,没有明确说明。通过对影响安全仪表系统运行阶段SIL的组织因素进行分析探讨,提出了一种解决安全仪表系统在运行阶段考虑人和组织因素的新方法,可以很好地预测操作SIL,并对最需改进的人和组织因素提供预防与纠正措施指导。
