基于残差注意力机制和子领域自适应的时变转速下滚动轴承故障诊断
2022-12-01董绍江裴雪武潘雪娇
朱 朋,董绍江,李 洋,裴雪武,潘雪娇
(重庆交通大学 机电与车辆工程学院,重庆 400074)
滚动轴承作为旋转机械的关键零部件之一,其健康状态直接关系到设备的运行可靠性,一旦发生故障,将可能对人员安全与经济效益产生巨大的影响[1]。通常,旋转机械由于功率时变而经常以时变的速度运行,且实际工作环境对轴承振动信号将会产生较大的干扰[2]。在时变转速、强噪音的变工况环境下采集到的滚动轴承振动信号存在特征漂移,传统故障诊断模型泛化性较差,需提出新的智能诊断算法。
阶次跟踪[3]是诊断时变转速轴承故障的主要方法之一,其主要步骤为转速提取、重采样、阶次频谱分析和故障诊断。但该方法受转速计安装位置和等角度重采样精度影响较大,针对此问题,高冠琪等[4]提出了一种基于时频挤压的转频估计方法;赵德尊等[5]提出了基于自适应广义解调变换的滚动轴承时变非平稳故障特征提取方法。但这些方法都存在不足:准确提取速度的时频算法在很大程度上依赖于信号处理技术的先验知识;即使能够准确提取出滚动轴承运行时的时变速度,也需要大量的专家知识才能准确诊断出是否发生故障。
近年来,随着计算机网络技术的发展,深度学习理论在故障诊断中受到了广泛的研究。An等[6]针对时变转速工况下滚动轴承的故障诊断问题,受无穷小思想的启发结合长短时记忆(long short-term memory,LSTM)网络,提出了基于递归神经网络的时变工况下滚动轴承智能故障诊断算法。Han等[7]针对转速波动对滚动轴承故障识别精度影响较大的问题,提出一种新的深度神经网络模型,主要创新是采用稀疏过滤提取振动信号特征,并将批归一化操作添加到每一网络层后以减少速度波动的影响。这些智能诊断算法获取较高准确率的前提是具有足量的含有标签的训练样本[8]。但是,在实际工业环境中,获取含有足量标签的故障样本费时费力,制约了神经网络在轴承诊断中的应用。
针对以上问题,迁移学习把少量含有标签的源域知识迁移到无标签的目标域中,使得网络模型具有较好的泛化性、鲁棒性。Li等[9]提出了基于卷积神经网络(convolutional neural networks,CNN)的深度迁移框架,通用特征提取器采用多层卷积神经网络,特定任务自适应层采用多核最大均值差异(multi-kernel maximum mean discrepancies,MK-MMD)度量准则进行源域与目标域的自适应。较多学者[10-11]针对变负载工况下轴承的故障诊断问题提出了迁移学习模型,并获得了较好的诊断效果。但是,强噪音环境对迁移学习任务的影响,以上文献未进行进一步研究。
针对滚动轴承待测样本在强噪音、时变转速的工况下诊断困难的问题。本文结合残差网络(residual neural network,ResNet)和通道注意力机制搭建了残差通道注意力弱共享网,进行通用特征的提取。在源域与目标域数据分布差异较大时,能使网络模型更好的学习目标域的特征。域自适应层采用局部最大均值差异(local maximum mean discrepancy,LMMD)度量准则进行源域与目标域的条件分布对齐,在强噪音、时变转速条件下模型具有较好的泛化性、鲁棒性。
1 所提方法理论背景
1.1 问题描述
1.2 残差网络(ResNet)
在卷积神经网络中,随着网络层数的加深,将会面临梯度消失、性能退化等问题。针对该问题,学者He等[12]提出深度残差网络,通过跨层连接来抑制网络加深过程中出现性能退化的缺点。残差单元结构图如图1所示,假设其神经网络的输入为x,期望输出为H(x),直接将x跨层到后面作为输出结果,则学习目标变成为F(x)=H(x)-x。
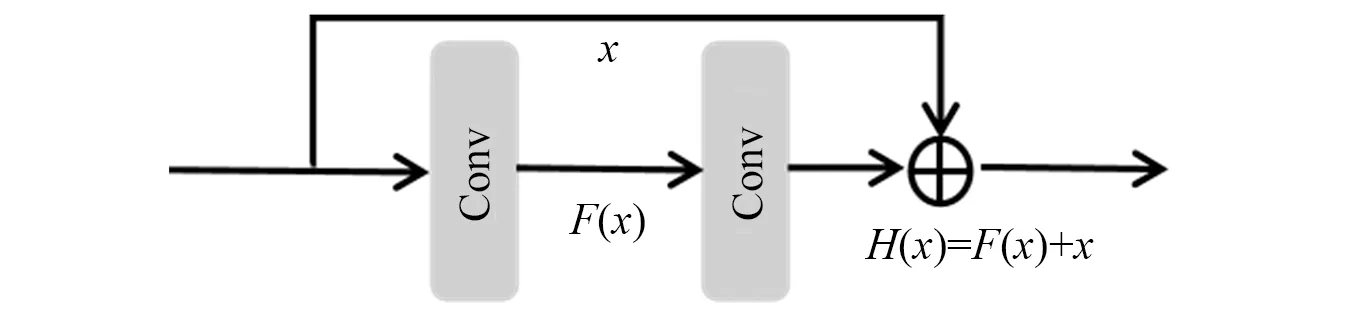
图1 残差单元示意图Fig.1 Schematic diagram of residual unit
1.3 最大均值差异
为了实现源域和目标域之间的领域自适应,需要相应的测试统计量来度量分布差异[13]。其中一种较常用的统计量是最大均值差异(maximum mean discrepancy,MMD),该统计量是度量两个数据集分布差异的非参数距离指标。源域数据集Xs和目标域数据集Xt之间的MMD的平方被定义为

(1)
式中:H为再生核希尔伯特空间(reproducing kernel Hilbert space,RKHS);φ∶Xs,Xt→H及K(·,·)为高斯核函数。
(2)
式中,σ为核宽度。
2 残差注意力机制和子领域自适应的滚动轴承故障诊断模型
考虑强噪音、时变转速下滚动轴承振动信号数据特征分布存在漂移,待测样本不含标签,传统深度学习模型泛化能力差。本文结合残差网络和注意力机制的特点,提出了迁移学习通用特征提取网络,即残差通道注意力弱共享网络;自适应层采用LMMD度量准则减小源域与目标域的条件分布差异。
2.1 通道注意力弱共享模块
现有的大多数领域自适应研究都采用强共享通用特征提取网络进行迁移特征的提取,并通过相应的度量准则减少特定任务层中的领域域差异。但是,当源域与目标域分布差异较大时,完全采用强共享网络模型的方法会造成神经网络模型过多学习源域与目标域不相关的特征,不利于目标域的迁移学习。因为较强的源域监督学习,网络将提取更多与源域相关的特征,而弱化目标域的特征,从而阻碍了领域特定的特征表示学习,并导致目标域分类错误。
为解决上述问题,本文引入通道注意力弱共享模块(channel attention weak sharing module,CAWSM),通过保留源域可迁移信息的同时抑制每个领域的无用信息,促进卷积层中的特征重新校准。
本文构建的通道注意力弱共享模块如图2所示。参考文献[14]通道注意力网络搭建方式。首先,将中间层源域和目标域特征嵌入表示为{Xs,Xt}∈H×W×C,其中H,W分别为空间尺寸的高度和宽度,C为通道数。每个域生成通道描述器为d∈1×1×C,对{Xs,Xt}进行全局平均池化以提取每个通道中的整体信息
(3)
式中:dC为第C个通道所有像素的平均值;(i,j)为位置坐标。

图2 通道注意力弱共享模块Fig.2 Channel attention weak sharing module(CAWSM)
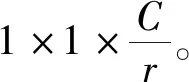
ωs/t=σ{FC[ReLU(FCs/t(ds/t))]}
(4)
式中:σ(·)=1/(1+e-x)为Sigmoid函数;FC(·)为共享FC层,用于增维的线性变换,而FCs(·)和FCt(·)为源域和目标域的单独降维变换。注意力权重ωs,ωt反映了跨域通道的重要性。
然后,通过在通道上将原始特征Xs,Xt分别与多个通道权重相乘来获得激活的特征映射,其公式为
(5)
若将图2中全局池化后源域与目标域共享一条数据特征流路线,即为通道注意力强共享模块(channel attention strong sharing module,CASSM),相关理论公式与上述类似。
2.2 残差注意力机制和子领域自适应的滚动轴承故障诊断模型
本文结合残差网络和通道注意力机制所提出的强噪音下时变转速无监督迁移学习网络模型,如图3所示。卷积层运算后均进行批归一化(batch normalization,BN)和线性激活(ReLU)操作,图中进行了省略。本文提出的通道注意力弱共享模块与残差网络的跨层连接形成了残差通道注意力弱共享模块,如图3中所示的3个残差注意力块。自适应层选择为全局平均池化后的全连接层,如图3右上所示,度量准则采用LMMD。
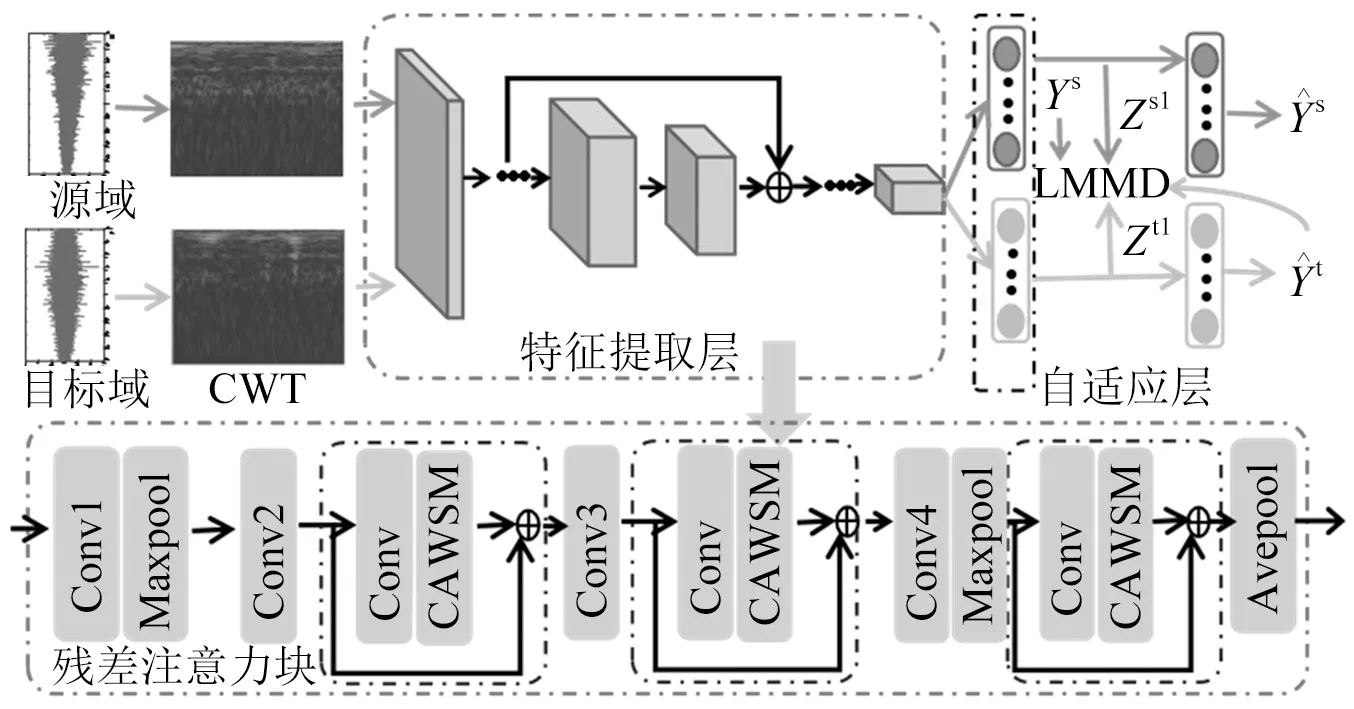
图3 所提方法故障诊断网络结构Fig.3 The proposed method fault diagnosis network structure
本模型的主要诊断流程:首先,将采集到的一维时变转速振动信号利用连续小波变换(continuous wavelet transform,CWT)生成源域与目标域图像数据集;其次,利用本文提出的网络结构进行浅层可迁移特征提取;然后,采用LMMD自适应度量准则进行网络自适应层的源域与目标域的条件分布差异匹配;最后,进行滚动轴承不同故障种类的诊断、识别,并分析不同模型的诊断效果。
训练过程中优化的目标函数为
(6)

(7)
式中:m为当前训练步数;M为总的训练次数。
2.3 子领域自适应函数
作为两个数据特征分布之间的非参数距离估计,基于MMD函数的域自适应方法主要是学习全局域移动,即对齐全局的源域分布和目标域分布,没有考虑全局域中两个子领域之间的关系(条件分布),导致迁移学习性能不理想,没有捕捉到细粒度信息[15]。针对该问题,引入局部最大均值差异
(8)
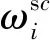
(9)
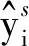
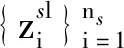
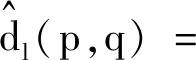
(10)
式中,zl为第l层(l∈L={1,2,3,…,|L|})的激活。
3 试验验证
为了进一步验证所提方法的有效性与优越性,对变速运行的轴承进行试验验证。试验装置如图4所示,由交流驱动器控制变速电机驱动转轴旋转。试验装置安装有两个轴承来支撑轴,左侧的轴承是健康的,右侧的轴承为不同故障状态下的试验轴承,分别进行试验,即有外圈缺陷、内圈缺陷、滚动体缺陷、复合故障和健康的5类状态的轴承,其中复合故障是内圈、外圈和滚动体的综合故障。右侧轴承壳体上安装有加速度计,用于收集振动信号。
试验所采集的一维振动信号总共有60个数据集,对于每个数据集,有两个试验设置:轴承健康状态和变速状态。运行转速状态为增速度、减速、增速度后减速、减速后增速度4种变速状态,每种变速状态下每类故障轴承做三次试验。采样频率均为200 kHz,采样持续时间为10 s[16]。
3.1 时变转速轴承故障数据集描述
选取数据集中转速数据进行分析,不同变速阶段转速的变化情况,如图5所示,轴承故障状态的振动数据具有时变特点。与恒速相比,时变转速下采集到的振动信号幅值随转速的增加而变大,如图6所示。
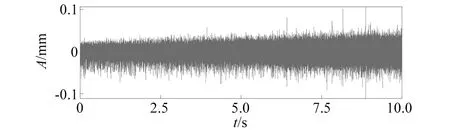
图6 加速下滚动体故障信号Fig.6 Rolling element failure signal under acceleration
3.2 连续小波变换时频图集生成
由于一维的振动信号样本长度的局限性,存在输入数据量不足的问题而影响模型诊断精度。小波时频图具有较好的时频分辨能力,可提供振动信号的时域、频域特征,故将一维振动信号采用连续小波变换生成本文故障诊断模型所需的图像集。
图像集的生成过程如图7所示。首先,因传感器采样频率较高为200 k,为包含丰富的时域信息,本文从原始振动信号中选取10 240个连续采样点为一个样本;其次,使用CWT将选定的10 240个点转换成时频图像,小波基选择为cmor3-3;最后,因轴承故障引起的共振频率主要在低频段,故时频图的频率范围设置在0~10 k,将时频图像灰度化并转换为模型可输入的三通道灰度图,图片大小为224×224×3。数据选取过程中采用滑动窗口的形式,连续两段数据相差6 000个数据点,即重叠区为4 240个数据点。
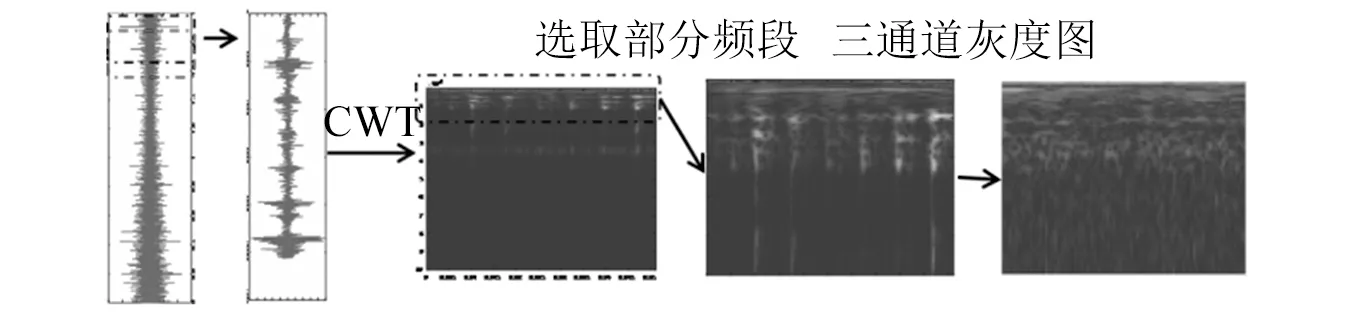
图7 生成灰度图的流程图Fig.7 Diagram of the process of generating grayscale images
为进一步说明CWT的优越性,采用短时傅里叶变换(short-time Fourier transform,STFT)进行对比分析说明,将不同方法生成的时频图采用典型的CNN网络(3.3节中的模型M1)进行分类识别,诊断精度如表1所示。由表1可知,STFT由于时频窗口固定,时频域内的故障信息分辨率较低难以完全展现时频域信息,导致CNN模型诊断精度较低。采用CWT的时频图集方法在两个迁移任务中均获得较高的识别精度,说明了本文CWT的时频表达的优异性。试验中详细细节见3.3节。

表1 不同时频图生成方法的诊断精度Tab.1 Diagnosis accuracy of different time-frequency diagram generation methods %
3.3 迁移故障诊断性能分析
为验证本文算法的有效性与优越性,将进行对比试验验证分析。表2为本文所提模型网络结构参数表。
对比模型一(M1)为传统的卷积神经网络模型CNN,主要含有三层卷积操作,每层卷积后进行BN、ReLU及步长为2的最大池化操作,最后为两个FC全连接层。
对比模型2(M2)为图像集预训练ResNet-50,在全局池化后添加两层全连接层进行微调迁移学习。
模型6(M6)为本文提出的方法,详细网络结构参数如表2所示。
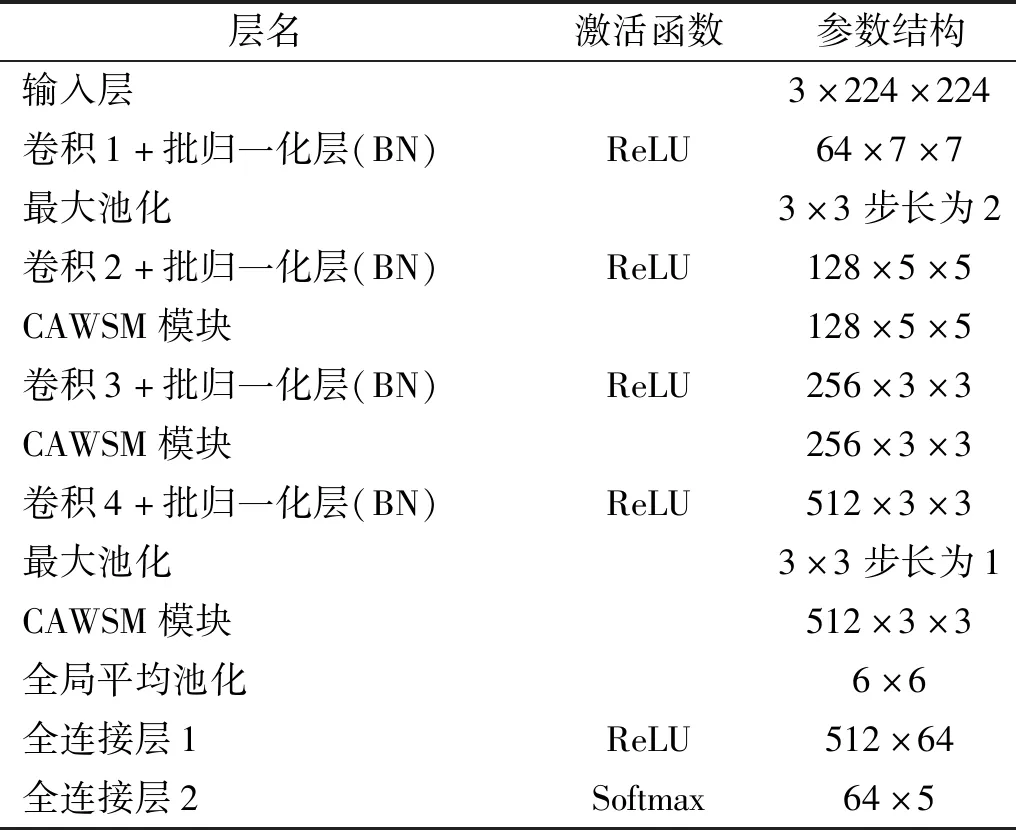
表2 所提模型网络结构参数表Tab.2 The proposed model network structure parameter table
对比模型3(M3)是将M6模型中的自适应度量准则替换为MMD,其余网络结构保持不变。
对比模型4(M4)是将M6模型中的自适应度量准则替换为Coral,其余网络结构保持不变。
对比模型5(M5)是将M6模型中的通道注意力弱共享(CAWSM)模块替换为通道注意力强共享(CASSM)模块,即通用特征提取层为强共享网络结构。
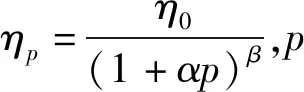
3.3.1 试验一:不同变速状态下迁移故障诊断
在工程实际中,由于机械设备功率的变化会造成轴承运行在波动的速度下,因此,源域与目标域为不同时变速度下采集到的振动信号。为模拟迁移学习任务,根据不同的变速情况分为4个全局域(IN、DE、INDE、DEIN),每个全局域包含5类状态数据,即5个子领域,分别为正常(NO)、内圈故障(IF)、外圈故障(OF)、滚动体故障(BF)、复合故障(CF)。每种故障类型生成300个灰度图像样本集,即每种变速阶段共含有1 500张灰度图。不同模型诊断平均精度及标准差如表3所示,迁移任务IN→DE表示IN为源域,DE为目标域。
不同模型的诊断精度结果如表3所示。由表3可知,所有模型中CNN诊断效果最差,一方面,是三层的卷积网络难以提取深层次故障特征;另一方面,采用域自适应迁移学习故障诊断方法,可以将源域学习到的知识直接传递给目标域,提高模型的故障诊断效果,故方法3~方法5诊断效果较好。在所有对比方法中,本文提出的方法在不同迁移任务中平均诊断精度最高,为99.85%,标准差最小,为0.18%,说明本文采用的域自适应度量准则LMMD通过匹配源域与目标域的条件分布差异,即采用软伪标签考虑不同子领域的分布差异。相对于MMD准则、Coral准则考虑全局域的边缘分布,具有更好的自适应性能,故本文提出方法相对于其他模型具有较好的泛化性能和鲁棒性。模型M1~M6的故障诊断的平均正确率均达到94.94%以上,主要由于每个模型中卷积运算后均进行了批归一化(BN)操作,BN操作能一定程度的抑制速度变化的引起的振动信号幅值波动。进一步通过对比模型M5和M6的诊断效果可知,本文提出的弱共享通用特征提取网络在强共享通用特征提取网络的基础上诊断率有所提高,主要原因是强共享网络结构存在过多学习源域,弱化目标域相关特征的不足,其较优的性能在后面的对比试验将进一步行说明。

表3 不同模型的诊断精度Tab.3 Diagnostic accuracy of different models %
3.3.2 试验二:强噪音、变转速状态下迁移故障诊断
在实际的工业生产环境中,被诊断的机械设备往往工作环境比较恶劣,采集到的信号容易受到其他设备或周围环境的影响,不可避免地带来噪音。但是,实验室的环境相对干净,所受到的其他干扰相对较少,采集到的振动数据受噪音的影响较小。因此,有必要研究本文提出的无监督迁移学习方法在嘈杂环境下的迁移性能。主要以目标域为DEIN的三个迁移任务为诊断对象,源域不添加噪音信号,目标域添加高斯白噪音信号,信噪比(signal-to-noise ratio,SNR)为-6~2 dB,详细细则参考Li等的研究。选择M2、M4、M5与本文所提方法M6进行对比分析,不同模型在不同迁移任务中的诊断精度如图8所示。
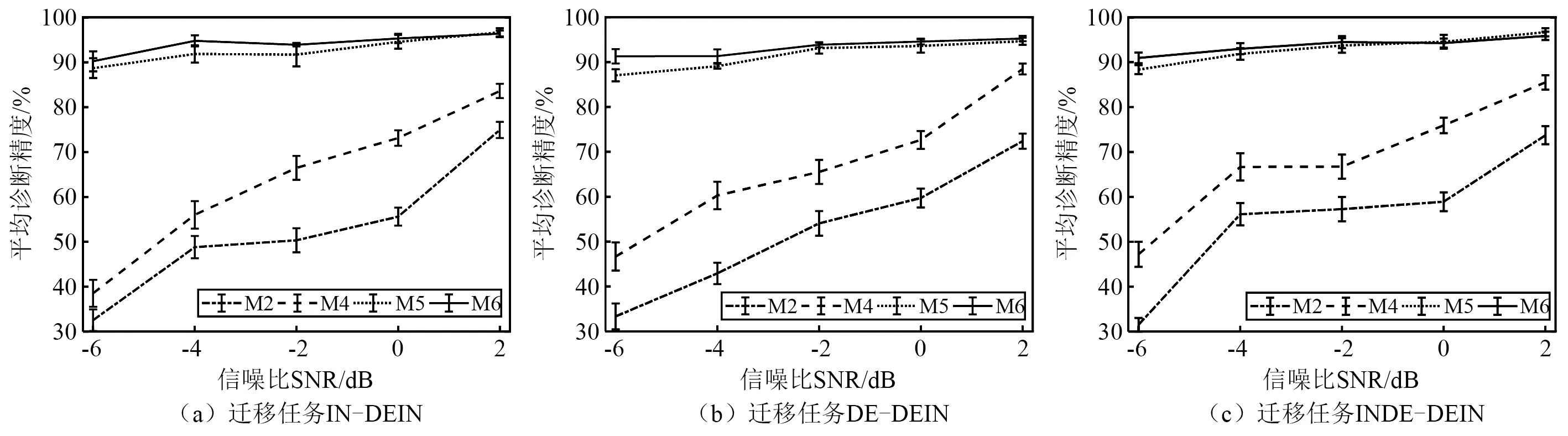
图8 强噪音环境下不同模型的诊断精度Fig.8 The diagnostic accuracy of different models in a strong noise environment
由图8可知,本文提出的方法在不同噪音水平下均能获得较高的平均诊断精度,信噪比在-6 dB以上时,平均诊断精度能保持在90%以上。源域与目标域含有一定范围的噪音差异时,模型的诊断精度波动相对较小,表明本文提出的方法在源域与目标域分布差异较大时,仍具有较强的泛化性、鲁棒性。
3种迁移学习任务中,模型M2的识别精度最低,一方面由于采用微调网络的迁移学习方法对不同噪音水平下时变转速故障诊断泛化能力较差,越强的高斯白噪音干扰,数据特征分布差异越大;另一方面本文提出的残差通道注意力弱共享模型不仅具有残差网络的特点,能在网络模型加深过程抑制梯度消失,还具有通道注意力机制的特点,能够实现不同特征加权表达的特点。弱共享网络结构更能有效提取强噪音环境下振动数据的故障特征,提高模型的平均诊断精度。
采用局部最大均值差异的迁移学习方法能较好的匹配子类任务的条件分布差异,捕获源域与目标域的细粒度差异,提高模型的诊断精度,而Coral度量准则在强噪音下匹配源域与目标域的效果较差,故M5,M6在所有迁移任务中诊断精度较高。
对比模型M5,M6可知,本文提出的弱共享通用特征提取层在源域与目标域差异数据特征分布差异较大时,效果提升效果相对较明显,在噪音水平为-6 dB时,两者分类精度相差4%左右。主要是弱共享通用特征提取层在学习可迁移信息的同时,可以抑制过多保留源域无用信息来促进卷积层中的特征重新校准,进而强化目标域的相关特征。
为进一步说明本文提出的迁移学习方法特征对齐能力,选取迁移任务INDE-DEIN中-2 dB噪音下4个模型进行t-SNE可视化操作,如图9所示。由图可知,本文引入的LMMD通过子领域自适应,能最大限度的分开不同种类的故障,但受噪音的影响,复合故障与滚动体故障、内圈故障存在混叠。
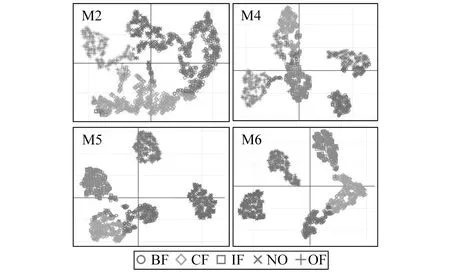
图9 -2 dB噪音下迁移任务INDE-DEIN的不同模型特征可视化Fig.9 Visualization of different model features of the transfer task INDE-DEIN under -2 dB noise
4 结 论
针对强噪音、时变转速下滚动轴承故障数据特征分布存在漂移、传统模型泛化性差的问题,提出了一种基于残差注意力机制和子领域自适应的时变转速下滚动轴承故障诊断无监督迁移学习方法,并进行了试验验证,得出以下相关结论:
(1)结合残差和注意力机制特点提出的残差注意力弱共享模型能有效提取出强噪音、时变转速环境下的故障特征,比仅用残差网络效果较好。
(2)本文提出的弱共享残差注意力机制通用特征提取模型相比于强共享策略,能更好的保留目标域相关特征,抑制网络模型过多学习源域的特征,能在源域与目标域数据特征分布差异较大时,更好进行源域与目标域的迁移学习。
(3)网络自适应层采用局部最大均值差异进行域自适应度量,通过利用伪标签以匹配不同域的条件分布,能较好的缩小子类任务的特征差异,捕获源域与目标域的细粒度差异,提高模型的诊断精度。
(4)通过不同模型在强噪音、时变转速工况下滚动轴承诊断性能的分析,验证了本文提出方法的优越性,且相比于其他模型具有较好的泛化性、鲁棒性。
