基于疲劳损伤谱的地铁车辆设备安装座铝合金焊缝加速寿命研究
2022-12-01陈宽裕阳光武肖守讷王举金
陈宽裕,阳光武,肖守讷,杨 冰,朱 涛,王举金
(西南交通大学 牵引动力国家重点实验室,成都 610031)
对于轨道车辆的设备来说,它们通常暴露于持续振动的环境中,这些振动载荷往往是确定性与随机性过程的组合[1],因此在产品研发的过程中,需要进行振动耐久测试来验证关键部件的振动疲劳性能[2]。目前对于车辆设备的台架试验,主要分为功能振动试验与模拟长寿命试验,长寿命试验需要在较短的时间内复现出整个服役寿命期间所产生的疲劳损伤,其具有较为重要的意义。
因此,频域载荷谱作为台架试验的加速度激励输入,其编制过程成为了试验中至关重要的一步,其中加速参数的选择以及等效加速时间的确定直接影响加速寿命的合理性。在工程问题中,许多载荷呈现明显的非高斯特征,尤其是在工况比较恶劣的环境下,激励的非高斯特性尤为明显[3],然而为简化计算,我们在分析时通常假设结构承受的随机载荷服从平稳高斯分布,这往往会导致疲劳损伤结果偏于危险,为设备服役埋下隐患[4]。目前国内外许多学者都对非高斯载荷的加速疲劳进行了研究,程红伟[5]建立了非高斯概率密度函数解析表达式,将概率功率谱与Dirlik公式结合,提出非高斯宽、窄带疲劳寿命计算公式,给出基于失效机理的随机振动加速试验方案。王得志等[6]研究了非高斯随机振动不同的分布特性,基于MSC二次开发提出一种非高斯信号数值模拟方法,并分析了加速疲劳寿命。高山[7]研究了海洋工程结构对于非高斯激励的响应规律,同时探究了其在非高斯激励下的疲劳损伤分布规律,提出了用于非高斯损伤频域评估的模态耦合分析方法。李向伟等[8]以40 t轴质量载矿石车为例,采集了重载线路的动态响应谱,采用同步缩小损伤量的加速试验方法,对数据进行处理和压缩,多轴加载实现了车体的加速疲劳试验。Wolfsteiner等[9]基于高阶谱计算多自由度系统(multiple-degree-of-freedom system,MDOF)下的FDS,以此来估算非高斯激励下多自由度系统的损伤,Wen等[10]以88 kW拖拉机前轴的负载信号作为输入,考虑载荷幅值和材料疲劳的影响后,提出了一种基于功率谱密度非高斯疲劳损伤谱编辑(power-density-based fatigue load spectrum editing,PD-LSD)的加速耐久测试方法,确保了该方法可以再现拖拉机组件的疲劳负载特性。Cianetti等[11]基于FDS以及测试合成的方法,对比了不同条件下加速度激励所产生的疲劳损伤,并通过一个耐久性测试案例验证了提出的非高斯加速方法。
常规的振动耐久加速试验通常会忽视激励信号的非高斯特性[12]。本文以车辆在实际线路运行时所采集到的加速度激励为例,提出了一种非高斯载荷的加速方法,计算支架模型加速寿命,并开展台架试验,将试验结果与仿真结果对比,验证了本文所提方法的有效性。
1 合成加速功率谱密度基本原理
频域内进行载荷谱编辑,首先需要判别输入激励的非高斯特性,计算各个工况或者任务段的疲劳损伤谱,接着线性叠加合成代表全寿命的疲劳损伤谱,基于损伤等效原则,最终通过公式计算加速功率谱密度(power spectral density,PSD)进行台架振动试验。
1.1 计算疲劳损伤谱
随机振动中引入带宽系数来判别窄带、宽带随机过程[13],计算公式为
(1)
式中,mn为n阶惯性矩。
假设应力服从窄带分布,即不规则系数r趋向于1,那么可以获得窄带疲劳损伤的表达式[14]
(2)
式(2)采用瑞利分布作为幅值概率密度函数,同时可对zrms进一步简化,如式(3)所示,可以推导疲劳损伤谱表达式(4)[15]
(3)
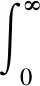
假设应力服从宽带分布,采用Wirsching公式与Dirlik概率密度函数分别计算宽带应力疲劳损伤谱,Wirsching修正疲劳损伤谱如式(5)所示
FDS=λRFDS(fn)
(5)
式中:λR为修正因子;FDS(fn)为Rayleigh假设下的疲劳损伤。
将Dirlik概率密度代入疲劳损伤求解通用公式可推导出宽带疲劳损伤谱表达式
(6)
式中:zrms为位移响应的RMS值;T为持续时间。
如果信号为非高斯信号且无法使用功率谱密度表示,则需要将信号通过单自由度系统获得其相对位移响应[16],再根据线性系统假设通过式(7)获得应力响应,改变系统固有频率,雨流计数绘制疲劳损伤谱。
σ=K·zp
(7)
1.2 频域合成加速谱
等效时间Teq内的合成加速试验PSD计算公式如式(8)所示[17]
(8)
式中:∑FDS(fn)为各工况总损伤;k为安全因子;Teq为等效试验时间。
2 台架试验加速PSD编制
本文以地铁底架天线安装座铝合金焊缝出现裂纹为案例,采集了车辆实际运行过程中上、下行的加速度激励数据,根据实际设计寿命进行加速处理,对比不同加速参数对加速功率谱密度的影响,最终合成台架试验加速PSD。本次加速度测点主要分布在底板、构架、枕梁、支架、轴箱等位置,选择车辆上、下行过程中构架附近加速度作为支架安装座的激励输入。
2.1 线路实测谱缩减
由于线路试验过程中存在比较多的停车与启动时间,该时间段加速度激励所产生的损伤较小可以忽略不计,所以需要根据时间关联损伤编辑法,对激励数据进行一定的缩减。时间关联损伤编辑法是以实测的局部应力应变数据为研究对象,计算测点的损伤-时间曲线,删除小振幅无损或者小损部分,压缩激励数据点,建立起较短的时间历程,进行具有代表性且有意义、更加经济的测试[18]。根据实际的情况选择合适的窗口长度与时间保留度,标记无损以及小损部分如图1所示,以第二次上行为例,缩减前后的加速度激励对比如图2所示。后续加速仿真计算均采用缩减加速度激励。
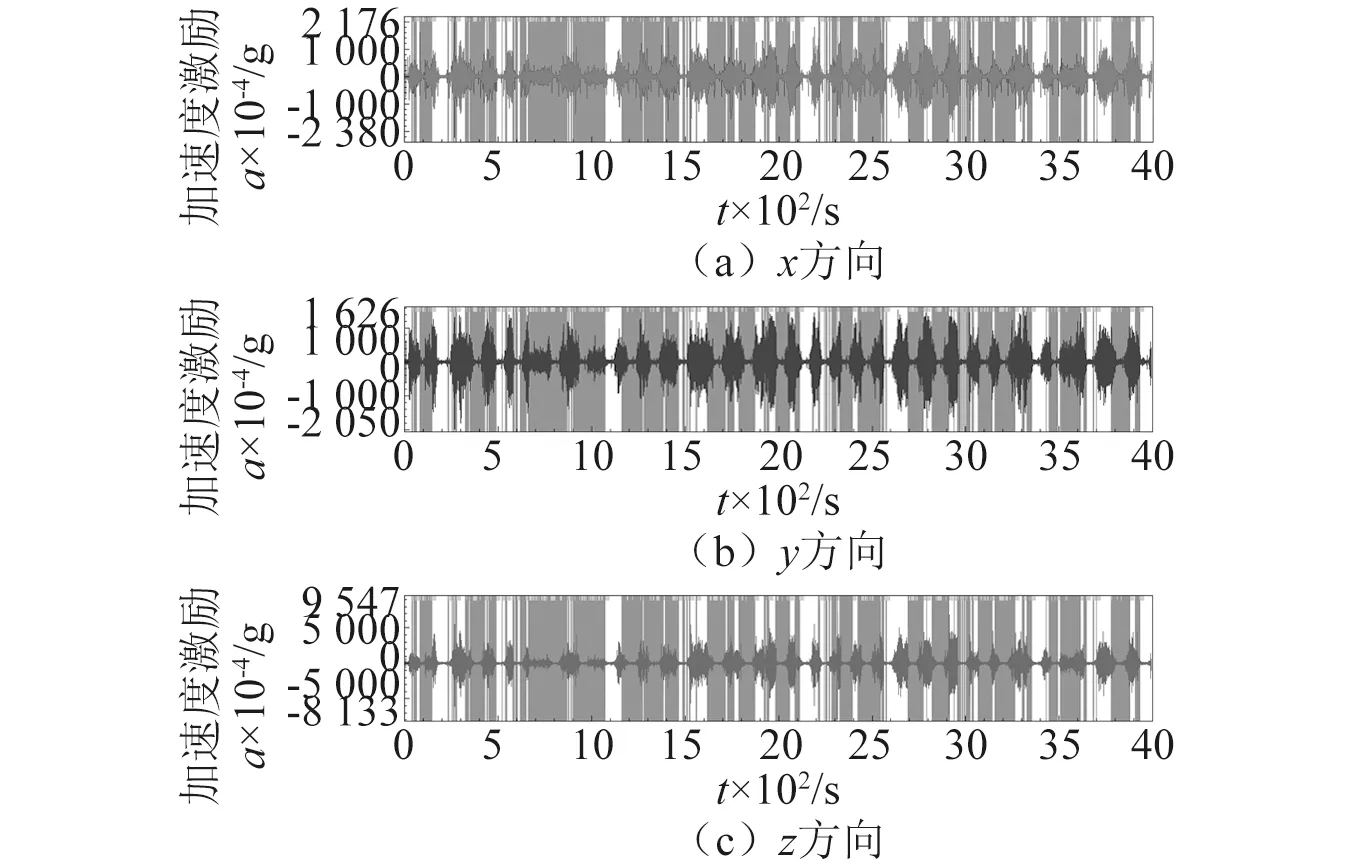
图1 标记加速度激励无损以及小损部分Fig.1 Mark acceleration excitation lossless and minor damage parts

图2 压缩原始加速度激励Fig.2 Compress original acceleration excitation
2.2 加速度激励输入与判别
功率谱密度是二阶统计量,对于均值为0的平稳高斯振动,PSD才可以包含随机振动统计特性[19];而对于非高斯随机过程,PSD所包含的信息还不够。车辆运行中设备所经受的载荷一般为非高斯激励,所以首先需要对输入激励进行非高斯判别。对于一个随机过程X,工程上常用偏斜度S和峭度K这两个参数来描述,其表达式如式(9)、式(10)所示
(9)
(10)
工程上来说,峭度K=3,偏斜度S=0时为高斯过程,K>3时为超高斯激励,K<3时为亚高斯激励。其次对加速度激励的幅值分布进行高斯分布检验,观察其幅值是否服从高斯分布,选择第二次上行任务段y向,以2.1节时域缩减加速度激励作为输入,分布检验结果如图3所示。每个任务段的峭度及偏斜度计算结果如图4所示。
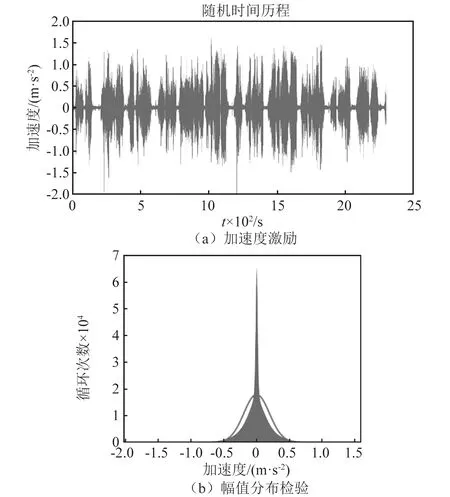
图3 输入加速度激励与其分布检验Fig.3 Input acceleration excitation and its distribution test
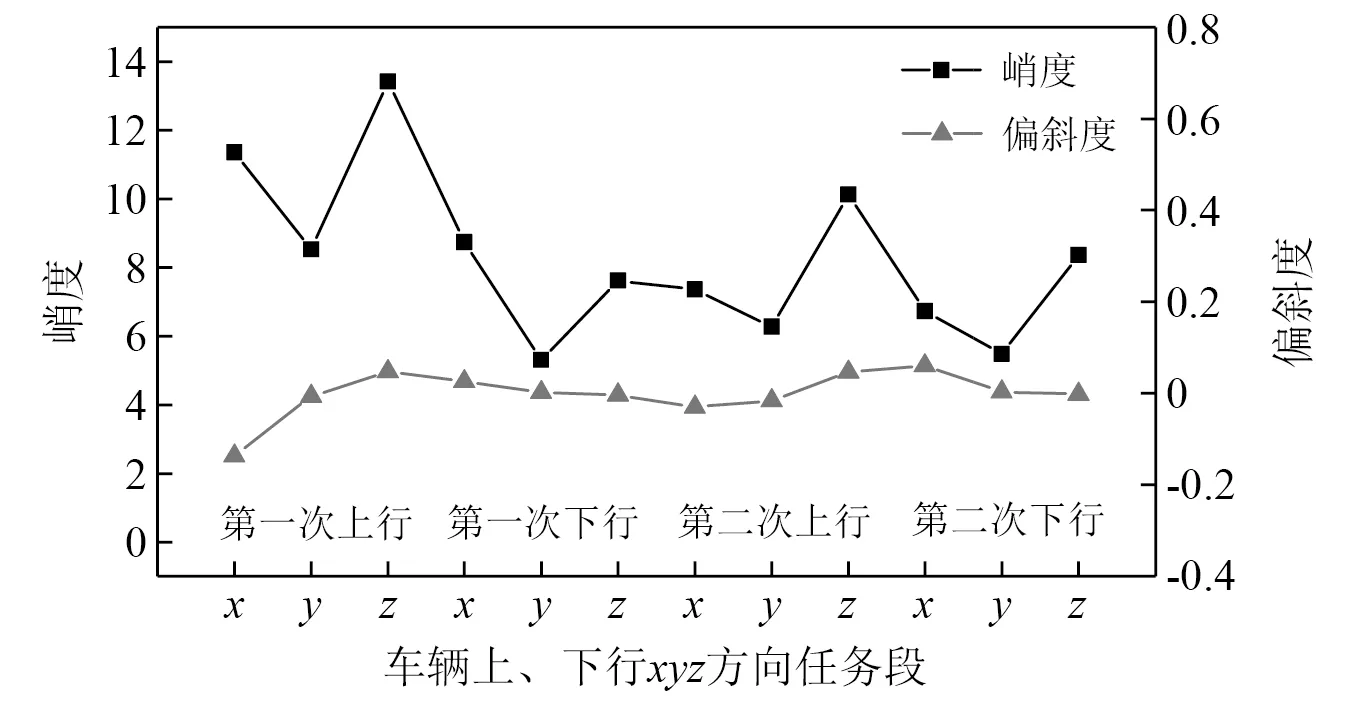
图4 车辆上、下行xyz方向的峭度、偏斜度计算Fig.4 Calculation of kurtosis and skewness of vehicle up and down xyz direction
经过对比分析,最终可以得出结论,若峭度大于4,可以在采集到的加速时间历程中观察到明显的突变峰值,可认为该激励是非高斯激励[20]。在车辆上、下行过程中,峭度最小为5.3,最大为13.42,综上在车辆运行过程中构架上的所采集到的加速度激励均为非高斯信号。
2.3 加速参数的选择
加速参数按照加速过程中计算所需可大致分为系统参数、材料参数、采样参数、疲劳损伤谱估算参数、等效加速时间等,不同加速参数的选择会给最终的加速寿命带来较大影响。
2.3.1 FDS计算方法的选择
首先对比激励通过SDOF系统后不同疲劳计算方法的选择对FDS的影响,以地铁第一次下行构架加速度激励为例,编程得到不同方法求解得到的三向FDS结果如图5所示,以时域方法获得的FDS以及加速PSD的RMS值为基准,可以发现Rainflow方法计算结果最准确,但其计算速度较慢,适合小数据量计算,简化Rayleigh方法计算速度最快,但由于其计算zrms时假设输入激励为白噪声,所以结果有较大偏差,频域方法求解FDS幅值普遍与时域雨流计数方法比较接近。根据2.2节中的激励判定结果,本文所有任务段激励均为非高斯激励,所以采用时域雨流计数法计算FDS并进行加速。
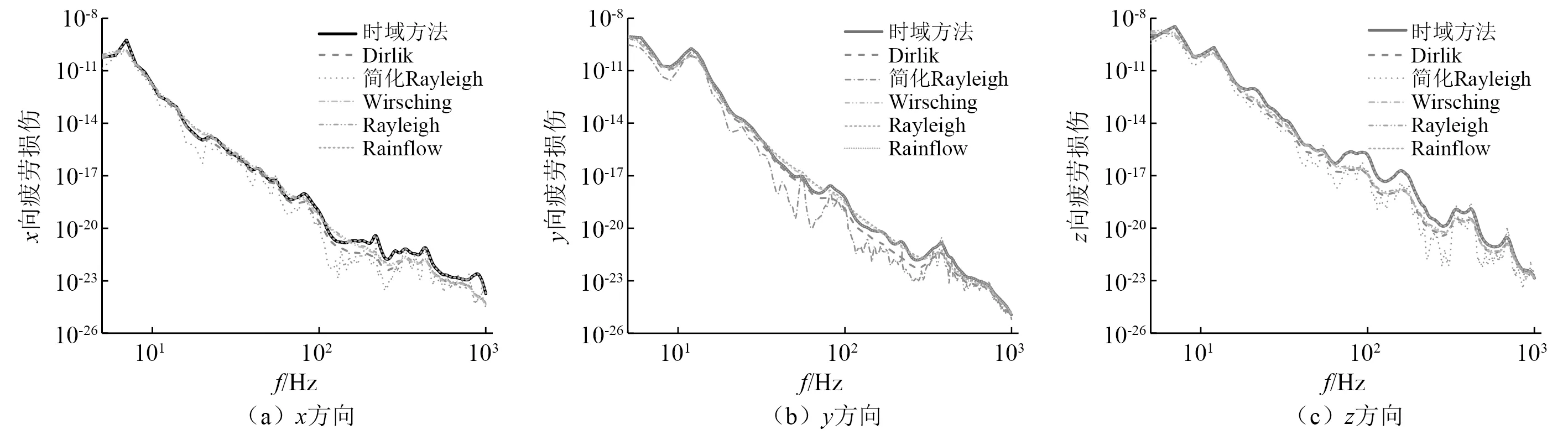
图5 三向不同计算方法FDS结果对比Fig.5 Comparison of FDS results of three-dimensional different calculation methods
通过对每种FDS求解办法耗时进行统计,如表1所示,可以发现频域方法虽然效率很高,但仅仅局限于各态历经的高斯激励,而时域方法求解精度高、耗时久,适用于非高斯激励。

表1 疲劳损伤谱计算方法优劣对比Tab.1 Comparison of FDS calculation methods
2.3.2 材料参数b的选择
本节改变系统参数(SDOF刚度K)和材料参数(S-N曲线中的b,C)绘制出加速PSD如图6所示,经推导以及计算结果可知,系统参数刚度K与材料参数C仅对FDS有影响而对最终的加速PSD与加速寿命没有影响,所以本节改变材料参数b,计算加速PSD。结果表明,b的取值对车辆上、下行加速激励有较大影响,可以认为b的取值越小,加速PSD的RMS值越大,反之越小。2.3.3节将从b的取值与等效加速时间综合考虑选择最合适的加速参数。
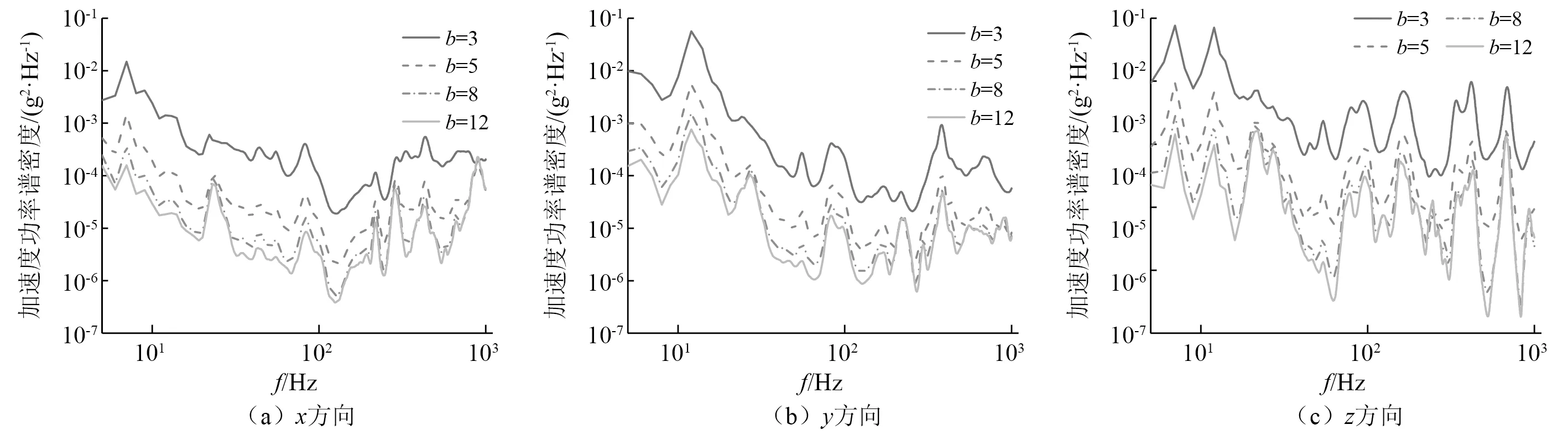
图6 三向不同b取值的加速PSD对比(时域方法)Fig.6 Comparison of accelerated PSD with different b values in three directions
2.3.3 等效加速时间的选择
改变预设定等效加速时间,计算加速PSD,通过预仿真计算加速寿命,与预设的加速寿命越接近说明加速效果越好,计算结果如图7所示。最终选择b=3.8,等效加速时间为5 h,可以发现此时加速寿命与预设加速寿命吻合最好。
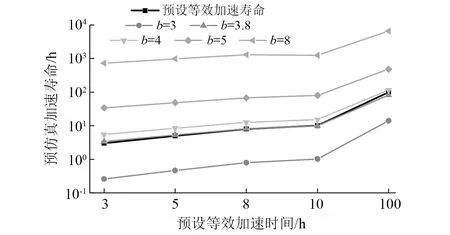
图7 不同预设等效加速时间下加速寿命Fig.7 Acceleration life under different preset equivalent acceleration time
2.4 合成频域加速PSD
经过上文对加速参数的选择,且根据车辆支架安装座实际设计寿命计算代表全寿命的FDS循环次数,最终根据式(8)可合成频率范围5~1 000 Hz的加速PSD激励,如图8所示。
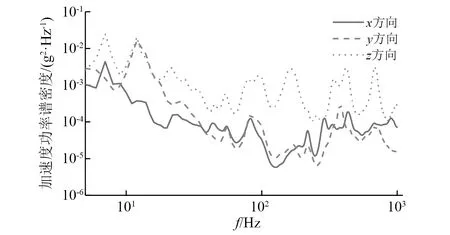
图8 三向加速PSD谱Fig.8 Three-dimensional acceleration PSD spectrum
3 焊接结构加速疲劳寿命
3.1 有限元模型
按照实际结构模型进行一比一建模,有限元模型与边界条件如图9所示。本文在仿真时主要计算加速激励对焊缝单元的加速疲劳寿命的影响,同时为减小计算量,在模型中设置set组包含贴片单元进行疲劳损伤求解,模型中施加加速度激励方法为大质量点法,由于加速度激励为PSD,所以损伤计算方法为谐响应法。本文测点均为铝合金搭接焊缝,根据EN-1999-1-3,5×106次循环次数处的疲劳强度σ-1=17.6 MPa,S-N曲线的存活率为97.7%
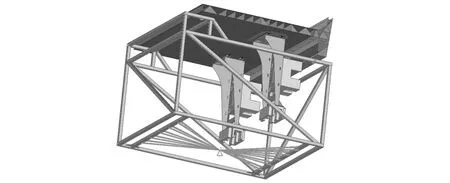
图9 有限元模型与边界条件Fig.9 Finite element model and boundary conditions
3.2 焊缝疲劳损伤计算
由于存在应力集中、焊接缺陷和残余应力的影响,焊缝处的疲劳强度会远远小于母材疲劳强度,所以为减小计算量,本文仅考虑焊缝的疲劳寿命而不考虑母材。选择所有焊址处的单元求解疲劳损伤,基于Miner损伤累积准则以及多轴线性累加法则可以得到所有焊缝单元的累积损伤值。加速后的危险测点的损伤云图(每秒损伤)如图10所示。改变材料参数b的值,观察所有测点单元的加速疲劳寿命,如图11所示。结果表明,加速疲劳寿命与b的取值有关,b取值越小加速每秒损伤越大,反之越小。

图10 支架安装座焊缝危险测点损伤云图Fig.10 Damage cloud map of weld danger measuring point of bracket mounting seat
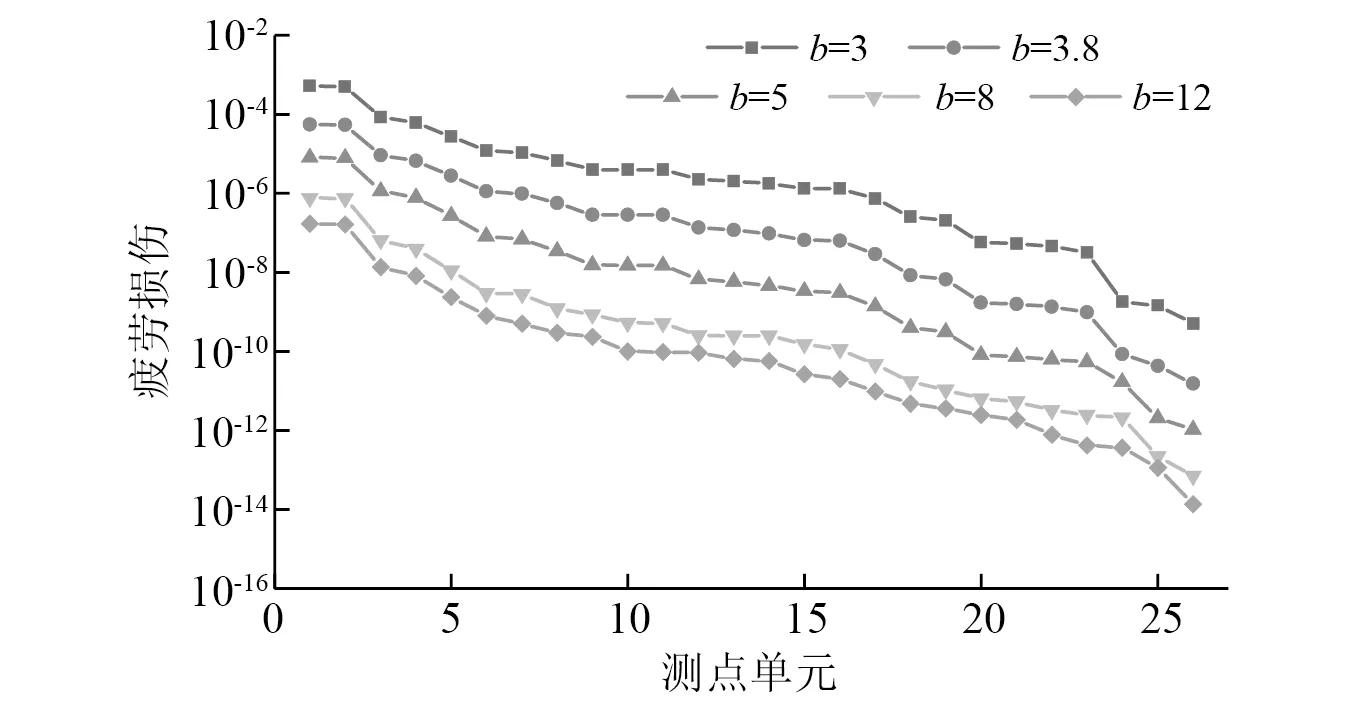
图11 谐响应法求解损伤结果(改变加速参数b)Fig.11 Damage results by harmonic response method(change the acceleration parameter b)
支架安装座焊缝单元较多,选择最危险的测点单元列出其加速累积损伤结果如表2所示,计算支架振动疲劳每秒损伤,乘以5 h后与损伤1相比较(假设支架损伤为1时产生疲劳裂纹并且失效),计算仿真加速累积损伤与原始损伤的相对误差,同时根据加速寿命与原始设计使用寿命,得到加速比(加速比=设计寿命/加速寿命),结果表明加速累积损伤的相对误差为0.57%,在允许的限值范围之内,加速比结果为21 722.26,这验证了本文加速方法的有效性。
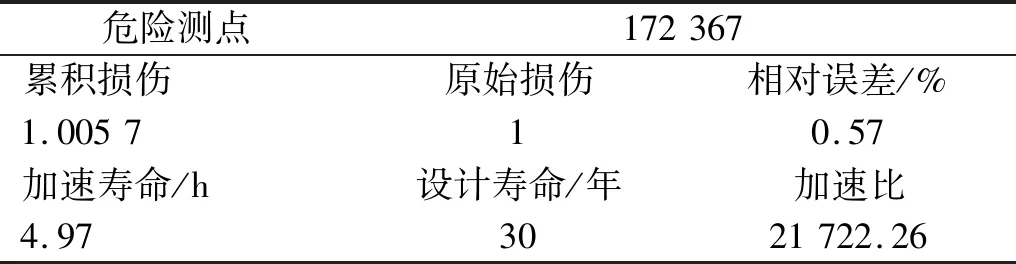
表2 加速前后疲劳寿命对比Tab.2 Comparison of fatigue life before and after acceleration
4 台架试验验证
为了进一步验证本文中非高斯激励加速方法的有效性,分别进行了3个方向的原始谱时域模拟试验、模拟长寿命试验,本次试验总共使用了8个三向应变花、8个单向应变片、6个加速度传感器一共50个通道。在试验先后顺序上,先进行线路实测谱试验,接着模拟长寿命加速谱试验,台架试验现场如图12所示。采用上文编制的加速PSD进行长寿命试验后,在天线支架安装座处未观察到明显裂纹。采集天线支架安装座焊缝危险测点处的应变响应如图13所示,基于Miner准则对台架试验所采集应变进行损伤累积,台架试验结果表明,采用本文非高斯激励加速方法可以模拟车辆设备在长寿命状态下的运行情况,对应变信号累积损伤结果与加速仿真误差在10%以内,说明可以通过加速5 h的PSD激励再现车辆设备长期服役的寿命状态,加速没有过度,天线支架安装座焊缝结构满足30年设计寿命要求。通过线路实测激励谱频域合成加速方法的关键原则为保证加速后的PSD激励没有加速过度,从而保证车辆设备结构的失效模式与线路实际运行过程一致,检验加速过度可以采用取极值响应谱与冲击响应谱的最大包络线与加速PSD极值响应谱对比的方法来检验。

图12 台架试验现场图Fig.12 Bench test site diagram
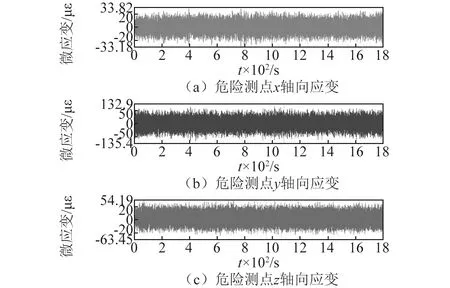
图13 采集危险测点应变响应Fig.13 Collect the strain response of the dangerous measuring point
本次台架试验可以较为精确地验证本文加速方法,后续还需进行大量台架试验,探究不同加速参数对安装座铝合金焊缝失效模式的影响。
采集台架试验中危险点的应变响应,计算响应的频域特性以及带宽系数,如表3所示。并且采用损伤累计法则计算累计损伤,与加速仿真结果对比,结果表明加速仿真与试验误差为-1.6%,在允许范围之内。
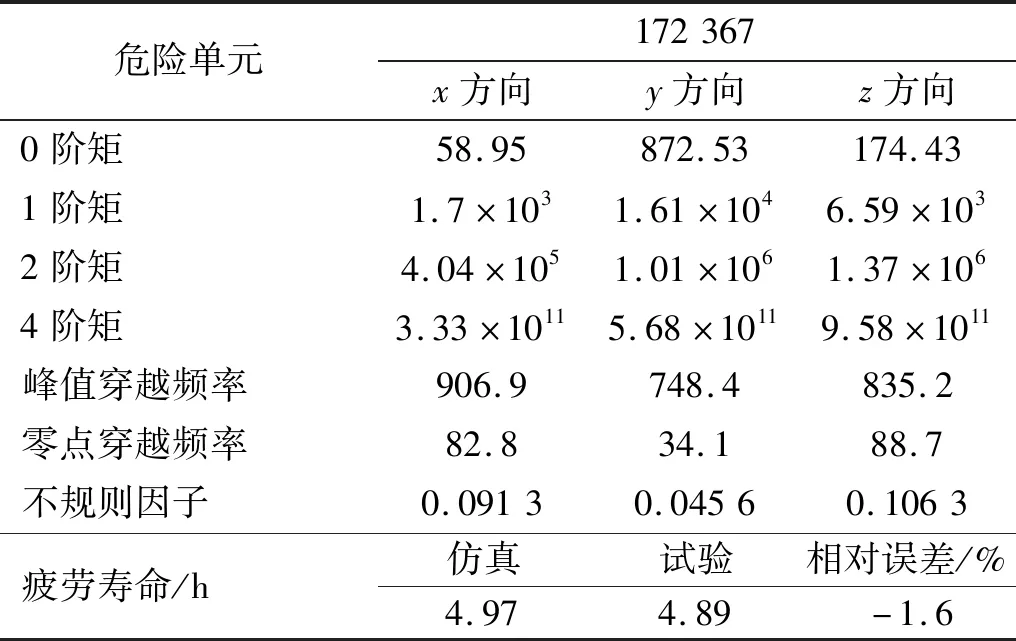
表3 加速试验频域特性以及仿真与试验疲劳寿命对比Tab.3 Frequency domain characteristics of accelerated test and comparison of fatigue life between simulation and test
5 结 论
本文基于疲劳损伤谱提出了一种处理非高斯激励的加速方法,以车辆天线支架安装座铝合金焊缝为研究对象,计算了加速疲劳寿命,并进行了台架试验验证,研究内容总结如下:
(1)本文首先以基于时间关联损伤编辑法的缩减信号作为激励输入,判别其非高斯特性,分别计算了每个工况xyz方向的峭度及偏斜度,同时,检验每一个任务段的高斯分布特性,绘制幅值分布图,最终得出结论车辆上、下行过程中加速度激励均为非高斯信号。
(2)对比了不同FDS计算方法的优劣,简化Rayleigh方法计算速度最快适用大量数据点计算,Dirlik计算精度最高,雨流计数方法对非高斯载荷适用,同时对比材料参数b与等效加速时间对加速PSD的影响,最终选择b=3.8,等效加速时间5 h。
(3)建立车辆底板与支架安装座局部有限元模型,改变参数b分别计算加速疲劳寿命,将加速寿命结果与原始设计使用寿命对比,其相对误差为0.57%,加速比为21 722.26,说明没有加速过度,且该加速PSD激励可以在5 h内反映30年的服役情况。
(4)开展模拟长寿命台架试验,试验结果表明,使用本文加速谱编辑方法,可以对非高斯激励进行加速,将采集到的支架危险点应变损伤累积结果与加速仿真疲劳寿命对比,相对误差为-1.6%,可以通过加速5 h的PSD激励再现车辆设备长期服役的寿命状态,同时也说明加速没有过度,为车辆其他设备的载荷谱编制提供了一定的参考。
