利用延迟反馈控制柔性圆柱涡激振动数值研究
2022-12-01徐劲力左红成
邹 琳,王 程,徐劲力,陶 凡,左红成
(武汉理工大学 机电工程学院,武汉 430070)
钝体周围非对称的漩涡脱落在结构上产生周期性的脉动压力,从而引发涡激振动(vortex induced vibration,VIV)现象[1-3]。当漩涡脱落频率接近结构固有频率时会发生大幅度的振动,导致结构疲劳损坏,也可以利用涡激振动产生新能源[4-5]。对于类似于海洋立管的柔性圆柱而言,由于展向具有柔性张力,涡激振动通常表现为更为复杂的驻波响应特性、行波响应特性和多模态振动特性等。
国内外学者对柔性圆柱涡激振动展开了大量数值及试验研究。早期数值研究主要是利用直接数值模拟方法求解N-S方程,以获得柔性圆柱的涡激振动响应,如Newman等[6]通过数值模拟方法研究了Re=100和Re=200下柔性圆柱的横向流振动,发现振动模式为行波与驻波混合响应模式;Lucor等[7]通过直接数值模拟研究了长径比超过500的细长圆柱在线型和指数剪切流流作用下的振动响应,研究认为指数剪切流速剖面会产生更大的振动频率范围,但和实际情况相比,圆柱单自由度振动具有一定的局限性。
Lie等[8]开展了剪切流作用下物理模型试验,研究立管长细比高达3 000,分析发现立管的振动响应是不规则的,具有一定的带宽,并且强度也随着带宽的不同有所变化。国内学者高云等[9]通过试验研究,深入研究了柔性圆柱体在剪切来流下涡激振动响应,发现当折合速度较小时,响应频率会全程参与涡激振动,随着折合流速的上升,响应频率则会间歇性参与涡激振动。宋磊建等[10]采用模型试验的方法研究了均匀流下柔性立管的涡激振动响应特性及涡激力载荷特性,研究发现均匀流下柔性立管的涡激振动响应为位移和主导频率不随时间变化的稳态响应。
对于大长径比的柔性圆柱体,数值模拟全尺度的振动响应存在一定的局限性[11-12],而试验方法研究成本相对较高[13-15],因此有必要建立一种能够快速预报响应细长圆柱涡激振动的经验模型方法模拟细长柔性体振动响应主要特征。尾流振子模型是应用较为广泛的经验模型。最早Noack等[16]利用范德波尔振子方程推导出能够预测细长钝体涡脱频率和角度的经验模型,利用带有扩散项的范德波尔方程能够准确预测出尾流脱落的定性特征。之后Balasubramanian等[17]在此基础上利用带有扩散项的范德波尔振子方程,用来预测均匀流和剪切流下直圆柱和锥形圆柱的漩涡脱落。Facchinetti等[18]利用尾流振子方程和结构柔性振动方程,研究了三维柔性圆柱的涡激振动响应,并与试验结果对比指出耦合模型能够准确预测涡激振动响应的振动形态。高云等[19-20]通过尾流振子模型,对线型剪切来流下两端铰接的细长柔性圆柱的涡激振动响应做了详细的探究。
综上所述,当前研究主要是对细长柔性圆柱的涡激振动响应进行研究,如何控制三维柔性圆柱涡激振动的研究相对较少。因此,本文借助尾流振子模型,提出利用延迟反馈来实现柔性圆柱涡激振动主动控制,研究延迟时间τ和延迟增益kd对柔性圆柱振动幅值和振动频率的影响,寻求控制柔性圆柱涡激振动的延迟反馈规律,为海洋立管等柔性钝体的振动控制提供有益探索。
1 数学模型
柔性圆柱流固耦合作用下产生振动幅值主要受到柔性体张力的影响,本文考虑无限长张紧圆柱在受到均匀来流作用下的涡激振动响应,忽略结构的弯曲刚度,模型示意如图1所示。

图1 受到均匀来流的无限长张紧圆柱Fig.1 An infinite tension cylinder subjected to a stationary uniform flow
图中,圆柱直径为D,长度为L,两端受到的轴向张力为N,在均匀来流Uf作用下产生振动,本文只考虑y方向的振动位移。参考文献[21],本文选取长径比L/D=25进行讨论。在延迟反馈控制的作用下,所选柔性圆柱部分的横向位移Y可以表示为
(1)
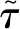
式(1)的右端项P(Z,T)为作用在结构上的流体力,可以表示为P(Z,T)=ρU2DCL0q(Z,T)/4,其中CL0为固定圆柱的参考升力系数[22],q(Z,T)是用来描述尾流运动的尾迹变量。φ(Z,T)=10-3sin(50πt)为初始位置函数,图2计算了不同初始位置函数φ(Z,T)下柔性圆柱纵向振动位移的均方值,说明数值计算结果与φ(Z,T)的选取无关。

图2 不同初始位置函数φ(Z,T)下柔性圆柱纵向振动位移的均方值Fig.2 RMS values of dimensionless displacements at different initial location function φ(Z,T)
尾流的运动可以用非线性振子来表示,常见的表示形式为范德波尔振子,写作
(2)
式中,A和ε为经验参数。引入无量纲参数y=Y/D,z=Z/D,t=TΩf,式(1)和式(2)可以写作如下无量纲形式
(3)
(4)

2 数值方法及模型验证
2.1 数值方法
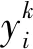
(5)
式中,k_d为延迟项所对应的索引,将式(5)代入式(3)、式(4)可以得到如下迭代格式
(6)
(7)
(8)
2.2 模型验证
首先对数值离散方法的时间步长和空间步长进行无关性验证。如表1所示,时间步长Δt取较大值0.02和0.03时,对于较小的空间步长Δz,数值计算结果发散。当Δt=0.005,Δz=0.05时,中间节点处最大振幅为1.849,而Δt=0.01,Δz=0.1时,最大振幅为1.847,降低约0.1%;当Δt=0.01,Δz=0.4时,最大振动幅值为1.785,降低约3.4%。因此在后续的数值计算中,取Δt=0.01,Δz= 0.1,整个数值仿真时间Tend=1 400。
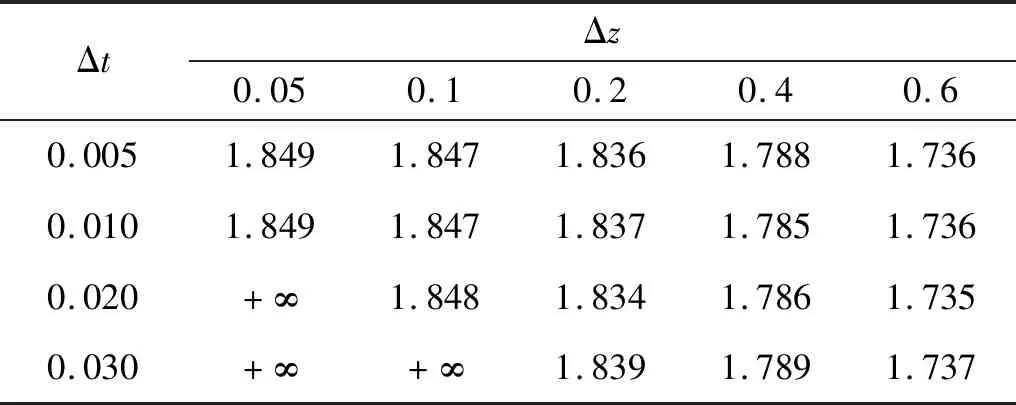
表1 不同时间和空间步长下,中间节点处结构振幅Tab.1 The vibration amplitude of cylinder at node under different space and time steps
为了验证文中所选模型的正确性,取L/D=25,c=4,μ=1.785,St=0.16,与Newman等所用参数保持一致。不考虑延迟反馈作用下,结构的振动位移云图如图3(a)所示,横轴的无量纲时间为t/2πSt。可以发现,在时间段200~240内,三维柔性圆柱的振动形式为驻波;当无量纲时间达到260时,振动形式由驻波逐渐向行波转变,此后一直保持行波振动状态,这一过程与Newman等DNS计算结果一致(如图3(b)所示),说明本文的计算模型是可行的。

图3 涡激振动位移响应对比(L/D=25,c=4,μ=1.785)Fig.3 Comparison of VIV displacement response with time and space (L/D=25,c=4,μ=1.785)
3 结果和讨论
3.1 延迟时间τ对振幅和频率的影响
从图4(a)~图4(d)均可以看出,在特定的延迟增益kd下,振幅随着延迟时间τ呈周期性变化,且每个周期内振幅最大值(定义为振幅峰值)保持不变,延迟时间τ并不能改变振幅峰值,其大小只与延迟增益kd有关,随着kd的增加,振幅峰值要更加偏离未施加延迟反馈时的振动幅值0.647,当kd为0.05,0.10和0.15时,振动峰值分别为0.85,1.18和1.82。从图4(a)可以看出,当延迟时间τ=0时,振动幅值分别为0.518,0.429和0.363,振动幅值随延迟增益kd的增大而减小,均小于未受控时的振动幅值0.647,最大能够降低43.9%。观察图4(b)~图4(d)可以发现,当kd符号相反时,振动幅值变化曲线之间会相差半个周期的相位。随着τ的增加,振幅最小值都大于τ=0时的振幅值,并且逐渐趋向于振幅峰值,而且随着kd的增大,趋向的速度越来越快,如箭头所示。综上发现,不同的延迟时间τ耦合不同的延迟增益kd,可以实现不同柔性圆柱振动幅值的控制,这将有益于实现工程实践中柔性钝体的振动控制。
如图5所示,振动频率随延迟时间也是呈周期性的变化,振动频率随着延迟时间τ的增加逐渐趋向于未施加延迟控制柔性圆柱振动频率f=0.156 4,且通过图5(b)~图5(d)可以发现,延迟增益kd越大,趋向的速度逐渐越快,如箭头所示。
3.2 延迟增益kd对振幅和频率的影响
图6(a)和图6(b)的延迟时间τ分别是图4(a)振幅取最大和最小时所对应的延迟时间。从图6(a)中可以看出,当kd由0逐渐增加时,振幅也逐渐增加,振幅只与kd有关。当kd从0逐渐减小,在τ取较小值(3.2,9.6和15.9)时,延迟增益对振幅的影响占主导,振幅随kd减小而减小;当τ取值较大的情况下,延迟时间对振幅的影响占主导地位,振幅随kd的减小呈现先减小后增大的趋势。在相同负值kd下,延迟时间越大振幅越大,这与图4所示振幅最小值逐渐趋向于峰值的变化趋势是一致的,而且kd越大趋向速度越快。由于延迟增益kd由正变负时变化曲线会相差半个周期的相位,因此图6(b)中振幅随kd的变化规律与图6(a)中所描述的规律刚好相反。
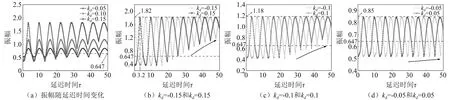
图4 延迟时间(τ)对振动幅值的影响Fig.4 The effect of delay time (τ) on the vibration amplitude
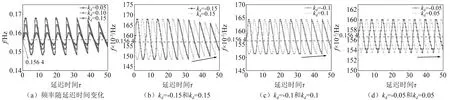
图5 延迟时间(τ)对振动频率的影响Fig.5 The effect of delay time (τ) on the vibration frequency
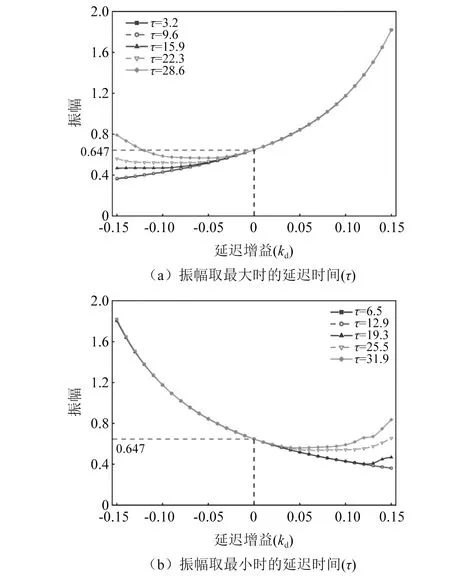
图6 延迟增益kd对振动幅值的影响Fig.6 The effect of delay gain (kd) on the vibration amplitude
为了探究柔性圆柱在延迟反馈作用下的能量转化,根据高云等的研究引入瞬时能量转化公式
(9)
式中,v(z,t),y(z,t)和q(z,t)分别为瞬时速度、位移和尾迹变量。瞬时能量W为正值表示流场向结构传递能量,从而激发柔性圆柱振动;负值表示结构向流场传递能量。
图7(a)所示为柔性圆柱中间节点处系统振动变量的值,可以发现未施加延迟反馈时变量q的最大值为4.821,当尾迹变量q增加时,振动位移y也相应增加。对于振动幅值较小的情况(τ=6.5)开始振动时间要小于振动幅值较大的情况(τ=3.2),而且都要小于未施加延迟反馈时的开始振动时间,说明施加延迟反馈控制能够降低系统的起振时间。图7(a)中瞬时能量W变化曲线表明,W的最小值越小,对应产生的振动幅值越大。例如对于τ=3.2而言,此时W最小值为-0.07,要小于τ=6.5时的-0.002,但前者对应的振动幅值y更大。结合瞬时能量W的含义,负值越小表明结构传递到流场中的能量越多,流场中能量增加会导致尾迹变量q值增大,从而又会反过来增加结构的振动y,因此通过能量云图7(b)可以看出,当τ=3.2时,由于能量在结构和流体中相互传递,驻波向行波演变的时间会增加(白色虚线框对应的时间),对于抑制振动的情况(τ=6.5),驻波向行波演变时间会减小。
上述可以发现瞬时能量W最小值对系统振动幅值增加或者减小有很大的影响。而结构振动增强的能量来源是外部延迟反馈控制系统,控制系统的延迟时间τ决定系统当前振动状态与τ时间之前振动状态之间的耦合关系,这种耦合关系会降低或者增加结构振动幅值。因此延迟增益kd决定了系统振动幅值的上限(振幅峰值),延迟时间τ决定系统当前振动状态与之前振动状态的耦合关系,结合图4(a)的结论,可以看出延迟时间τ并不能改变振幅峰值,峰值大小只与延迟增益kd有关。

图7 当kd=0.15时,延迟时间(τ)对系统的影响Fig.7 The effect of delay time (τ) on VIV system when kd=0.15
图8(a)和图8(b)中的延迟时间分别是图5(a)频率取最大和最小时所对应的延迟时间。从图8(a)中可以看出,当kd由-0.15逐渐增加到0.15时,对于延迟时间τ=1.4,τ=7.4和τ=13.4而言,振动频率随kd的增加而增加;当τ=19.4和τ=25.6时,振动频率先保持不变,kd进入正值以后频率逐渐减小,在kd=0.12时频率又突然增大,最终值和其他延迟时间保持相同。对于图8(b)而言,振动频率随着kd增大都呈现逐渐减小的趋势。
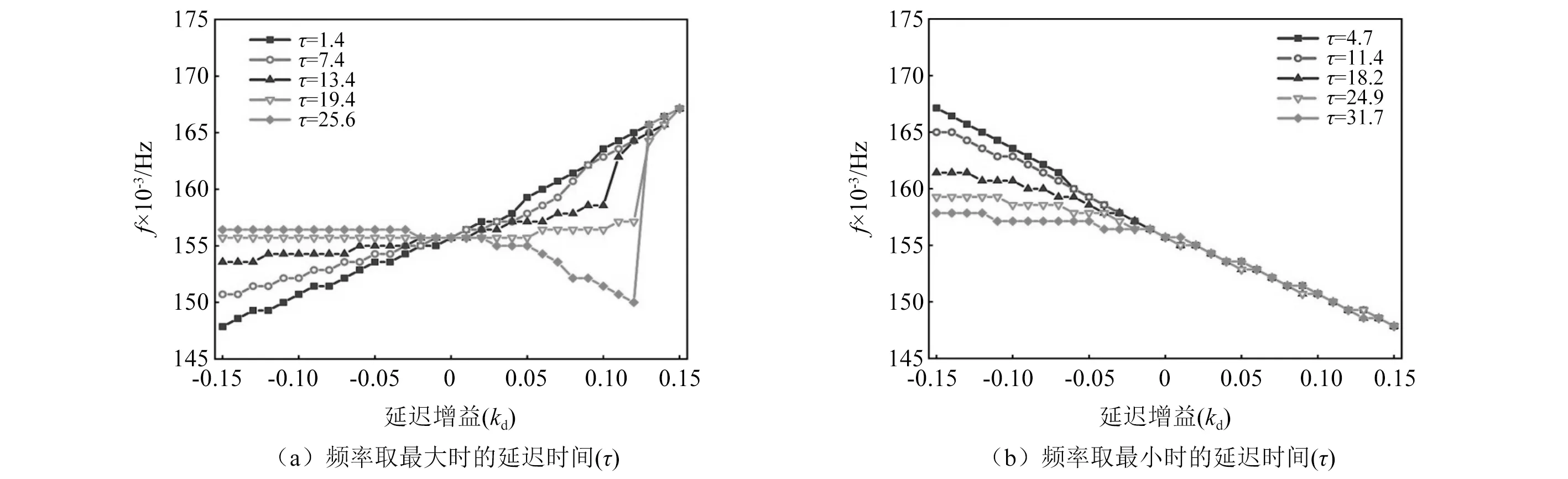
图8 延迟增益kd对振动频率的影响Fig.8 The effect of delay gain (kd) on vibration frequency
从图9可以发现,未施加延迟反馈控制时,振动幅值为0.647,行波传递周期为6.41,振动频率为0.156(1/6.41);当τ=4.7时,振动幅值增大为0.899,行波传递周期为6.71,振动频率减小为0.149;当τ=1.4时,振动幅值减小为0.521,行波传递周期为5.95,振动频率增大为0.168。相较于未施加延迟的情况,振动幅值和振动频率变化呈相反的趋势,振动幅值增大,振动频率就会减小。
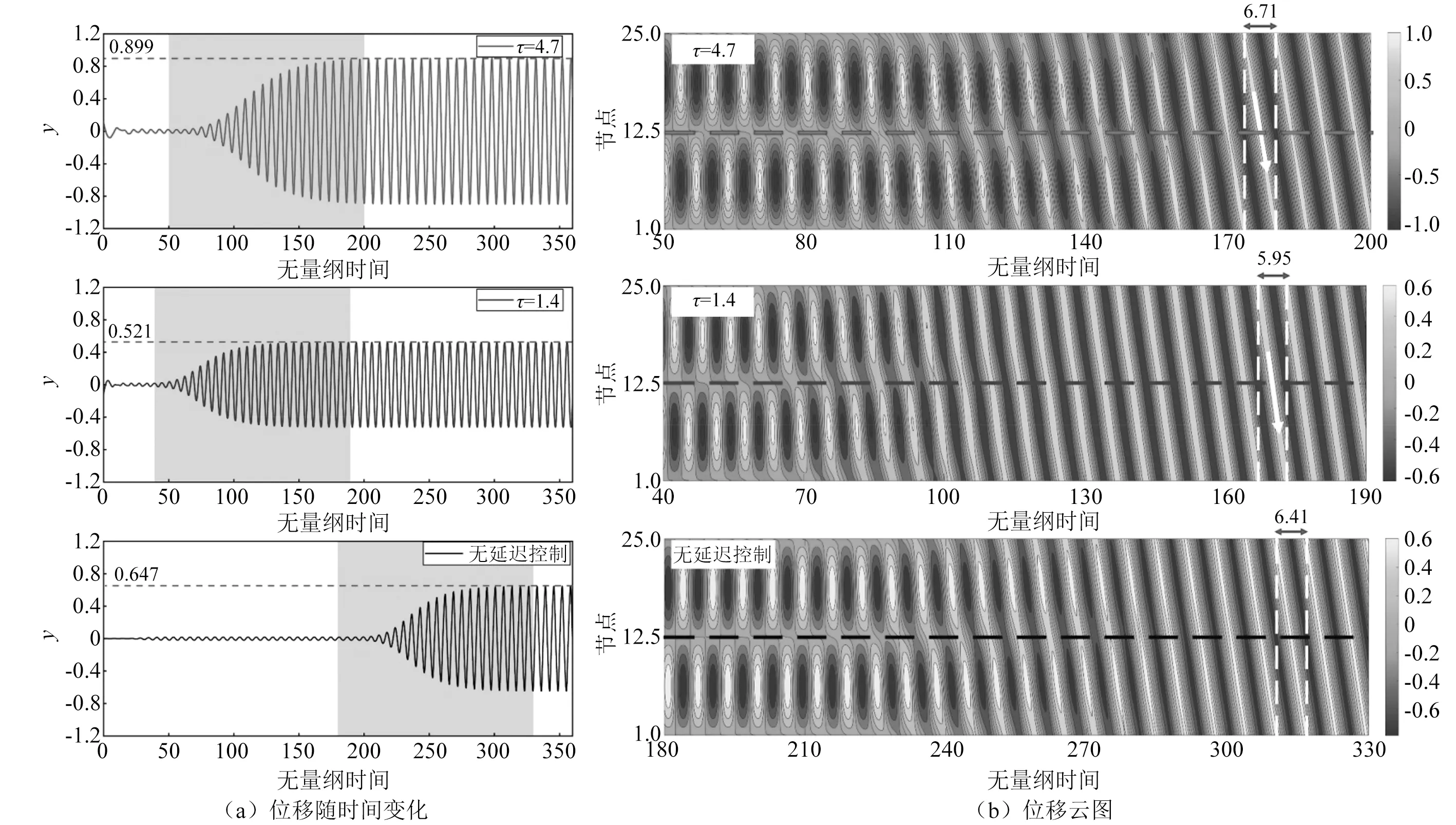
图9 振动位移和行波频率时间的关系(kd =0.15)Fig.9 The relationship between vibration displacement and frequency of travelling wave (kd =0.15)
3.3 理论解释
对于耦合方程式(3)和式(4),设方程组的解为谐波行波的形式,写作
y(z,t)=y0ei(kz-ωt-φ),q(z,t)=q0ei(kz-ωt)
(10)
式中:结构位移y和流体变量q都具有共同角频率ω以及波数k;φ为变量之间的相位角,y0和q0为与时间无关的幅值。将式(10)代入式(3)和式(4)中,得到
(11)
式(11)对角项分别为结构和流体的色散关系,写作
(12)
(13)
为了得到实数角频率ω和波数k,式(11)的行列式为0,由此得到流固耦合系统的色散关系为
DFS(ω,k;τ,q0)=
DS(ω,k;τ)DF(ω,k;q0)+AMω2=0
(14)
令式(14)实部和虚部为0,分别得到
-(ω2+c2k2)(-ω2+1)-
(15)
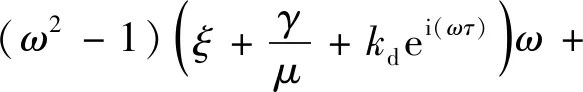
(16)
分析式(15)和式(16)可以发现,振动角频率ω、波数k以及尾迹变量q0与延迟参数kd和τ有关。首先不考虑延迟参数,得到角速度ω和q0随波数k的变化,如图10所示。可以发现,有无数个(ω,k,q0)组合满足上述两个方程,特定的组合与给定的边界条件有关。对于无限长柔性圆柱而言,最大的振动幅值y0和尾迹变量q0会发生在ω=1处,此时波数k=0.25,q0=4.89。
确定的尾迹变量q0之后,根据式(15)和式(16),ω和k与延迟参数相关。从图11中可以发现,随着τ的增加,频率f=ω/2π逐渐趋向于0.159,这一变化规律与图5中的变化规律一致,同时波数k也逐渐趋向于0.25。通过图11(c)可以看出,当τ较大时,ω/k的值基本保持为4不变,这与Facchinetti等研究中的结论ω/k=c相一致。通过上述分析发现,当延迟时间τ不断增加时,振动频率f和波数k都趋向于未受控时的值,分别为0.159和0.25。
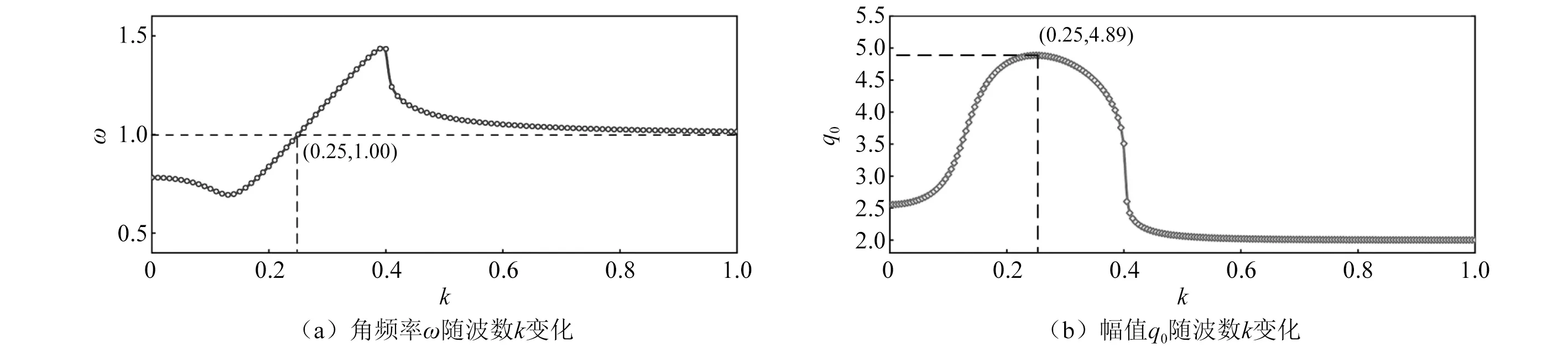
图10 振动频率ω和尾迹变量q0随波数k的变化趋势Fig.10 The variation of vibration frequency ω and wake variable q0 with wave number k
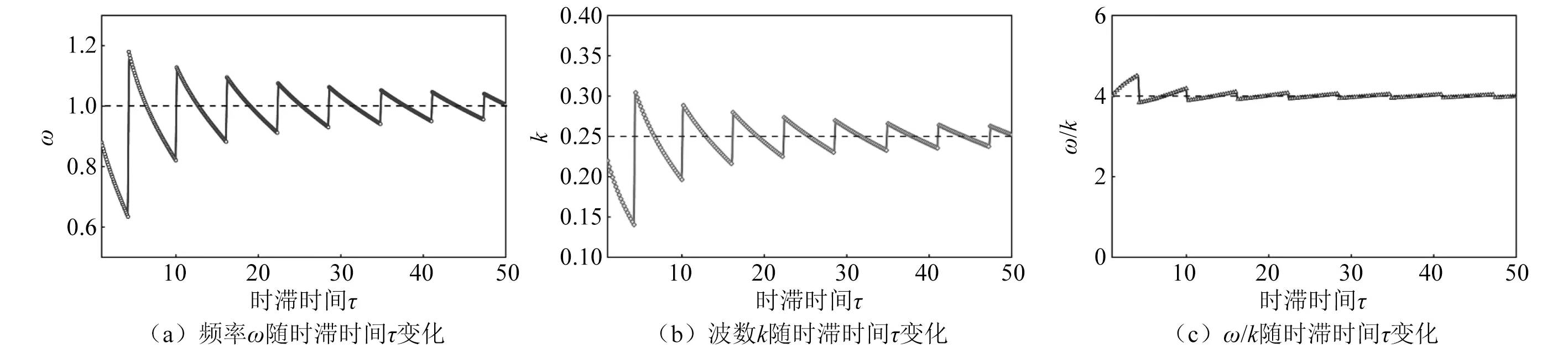
图11 频率ω、波数k以及ω/k随延迟时间τ变化规律(kd=0.15)Fig.11 The variation of frequency ω,wave number k,and ω/k with delay time τ (kd=0.15)
4 结 论
本文以三维细长柔性圆柱为研究对象,基于结构梁振动模型和尾流振子模型,利用二阶中心有限差分方法求解耦合方程,通过引入时滞反馈控制,讨论了在不同的反馈参数下(延迟时间τ和延迟增益kd)柔性圆柱涡激振动的幅值和频率变化情况。主要得出如下结论:
(1)探究了延迟时间τ对系统振幅和频率的影响,发现三维柔性圆柱振动幅值和频率随τ的增加呈周期变化;相反的延迟增益会使振幅变化曲线相差半个周期的相位角,而且系统能够达到的振幅峰值随着kd的增大而增大。
(2)探究了在特定τ下kd对系统振幅和频率的影响,发现延迟增益kd决定了系统振动幅值的上限;且振动频率和幅值的变化呈相反的趋势,振动幅值增大,振动频率越小。
(3)通过理论分析得出流固耦合系统的色散关系,发现振动频率ω和波数k随着延迟时间τ的增加最终会保持不变;振幅峰值只与延迟增益kd有关,kd越大振幅峰值越大。
