基于时域识别方法的加筋土挡墙动力特性研究
2022-12-01李思汉蔡晓光景立平张少秋徐洪路
李思汉,蔡晓光,黄 鑫,,景立平,张少秋,徐洪路
(1.防灾科技学院 地质工程学院,河北 三河 065201;2.河北省地震灾害防御与风险评价重点实验室,河北 三河 065201;3.中国地震局 建筑物破坏机理与防御重点实验室,河北 三河 065201;4.中国地震局 工程力学研究所 地震工程与工程振动重点实验室,哈尔滨 150080)
土工合成材料因可应用于环保、水利、交通、市政、建筑等多种基础领域而成为应用主流之一[1-3]。随着新基建、新城镇和重大工程建设战略方针的施行,杨广庆[4]预测:“中国土工合成材料行业市场在五年内的复合增长率约13.75%,到2025年时中国市场规模达到800 亿元”。作为使用土工合成材料的一类结构,可知加筋土挡墙(reinforced soil retaining wall,RSRW)必有广阔的应用前景。
相比于传统的重力式挡墙,加筋土挡墙具有施工简单快速、碳排放量低[5]、抗震性能优越[6]等优势。为在地震区内更好的推广加筋土挡墙结构,需对加筋土挡墙的动力反应进行全面系统的掌握。自振频率是抗震设计中的关键参数,决定着加筋土挡墙是否会与外部激励产生共振现象。众多学者利用振动台试验、理论分析和数值模拟三种手段对自振频率的解析式、影响因素进行了相关研究。
朱宏伟等[7]通过振动台试验得出包裹式加筋土挡墙的主频幅值比条带式加筋土挡墙大,进而提出包裹式加筋土挡墙的抗震性能较条带式加筋土挡墙更加优越的结论。朱宏伟等[8]对土工袋加筋土挡墙进行振动台试验可知,随着加载的持续进行,模型的自振频率降低,阻尼比增大;输入的地震动越强,自振频率的下降幅度越大。Huang[9]通过6 Hz和10 Hz正弦波对一系列返包式加筋土挡墙的主导频率进行了研究。
徐鹏等[10]以整体刚性面板加筋土挡墙为研究对象,分别用弹性地基梁模型、线性弹簧模型表示面板、填土及筋材,提出了一种加筋土挡墙固有频率计算方法,计算求得的基频值与既有瑞利能量法计算值具有较好的一致性。Xu等[11]利用传递矩阵法计算加筋土挡墙的固有频率,通过比较相关文献中解析和数值方法预测频率结果,验证了方法的准确性。
Ghanbari等[12]将土体等效为一系列的线性弹簧,提出了计算挡土墙固有频率的新公式。Sarbishei等[13]基于能量的高速同步算法来估计加速度沿墙高的分布情况,利用水平切片法和复质量-弹簧法确定了加筋土挡墙基频,并提出了加筋土挡墙基频的简单关系式。Ramezani等[14]基于弹性地基梁理论,提出了计算全高刚性混凝土饰面墙加筋土挡墙固有频率的解析解。考虑挡墙的刚性运动,给出了刚体变形模态固有频率的两个解析计算公式,同时,应用能量法建立了一种新的计算弯曲变形模式固有频率的解析公式。
伍永胜[15]利用ANSYS归纳了加筋土挡墙的一阶频率。Hatami等[16]总结部分自振频率计算公式(如Richardson和Lee),对影响加筋土挡墙模型基频的一些结构设计参数进行了研究和讨论,认为共振频率与地震动强度有关。
综上可知,众多学者将自振频率视为加筋土挡墙的整体频率,没有明确加筋土挡墙在不同高度、不同部位处的频率是否存在差别。共振频率随着地震动强度的变化规律并不清晰。在文献调研阶段,作者发现关于加筋土挡墙不同高度、不同加载阶段的阻尼比变化规律研究较少,部分规范[17-18]关于土体内加速度的放大情况与实际情况不符。针对上述问题,本文利用模块式加筋土挡墙振动台试验,研究了加筋土挡墙的自振频率和阻尼比的分布规律,并参考试验数据和GB 50111—2006《铁路工程抗震设计规范》提出了适用于模块式加筋土挡墙的加速度放大系数分布规律。研究结果可为模块式加筋土挡墙的抗震设计研究提供参考资料。
1 试验方案
1.1 振动台设备
在防灾科技学院的中国地震局建筑物破坏机理与防御重点实验室的室内双向电液伺服振动台上进行了测试。图1显示了研究中使用的振动台系统,其中包括一个3.0 m(L)×1.5 m(W)×2.0 m(H)的刚性模型箱。振动台的台面尺寸为3.0 m(L)×3.0 m(W),最大加速度为2.0g,最大承重为20 t[19-21]。

图1 振动台设备及刚性箱Fig.1 Shaking table facility with a rigid box
1.2 相似关系
为尽可能真实地反映实际工程的工程特性,考虑振动台的承载能力和模型箱尺寸,将模块式加筋土挡墙的相似常数定义为1∶4和1∶2。由于试验中无法满足所有参数的相似关系[22-24],故需根据试验目的重点关注主要参数,忽略次要参数。根据Iai提出的相似准则,推导出模型试验的主要相似参数,如表1所示。
1.3 回填土
回填土采用级配不良的中砂(D10=0.18 mm,D30=0.29 mm,D60=0.37 mm,Gs=2.86,Cu=2.06,Cc=1.26),其级配曲线如图2所示。通过相对密度试验测得最大干密度为1.99 g/cm3、最小干密度为1.52 g/cm3,相对密度为0.7时的回填土密度为1.82 g/cm3。对于特定9.3%含水率的三轴不固结不排水试验和固结不排水试验,采用以下步骤进行制样:①在烘箱内将砂铺开烘干6~8 h;②按照含水率将水添加到标准砂试样中,搅拌均匀;③附上保鲜膜放入干燥缸,静置24 h后取出,测量试样的实际含水率值,实际含水率与设计含水率9.3%一致后采用分层击实法快速制备三轴试样。两种试验结果可知,回填土摩擦角分别为41°和37°。为严格控制相对密实度,回填土采用分层填筑压实,具体计算方法如下:①回填土晾干,通过最大最小干密度、相对密实度、每层填筑高度确定每层土体的质量;②采用压实工具对土体分层压实,以满足相应层高。方法与Wang等[25]采用的方法一致。
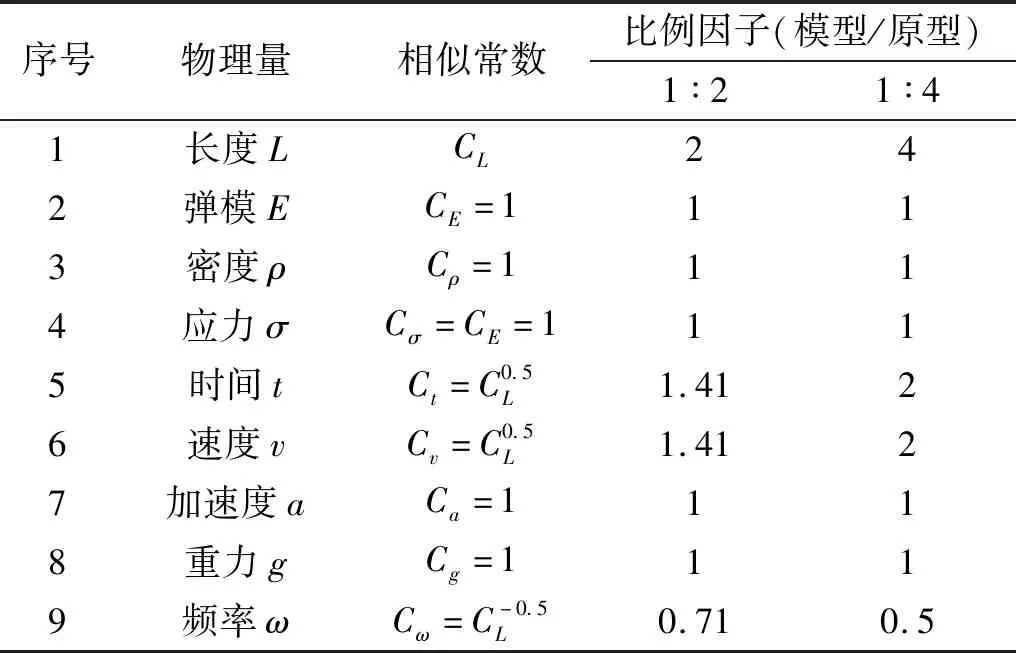
表1 模型试验相似常数Tab.1 Scaling factors in model test
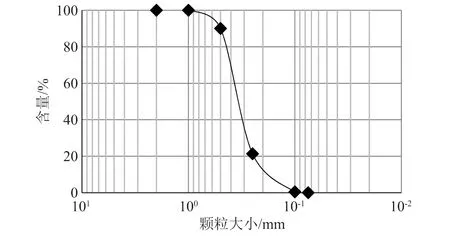
图2 颗粒级配曲线Fig.2 Grain size distribution curve
1.4 筋 材
筋材采用高密度聚乙烯单向土工格栅,拉伸单元长度为22.5 cm,横肋宽度为2.22 cm,土工格栅厚度为0.1 cm。参考ASTM D6637[26]进行试验可得,土工格栅的抗拉强度分别为T2%=17.4 kN/m和Tult=50 kN/m。试验模型采用与原型相同的筋材,原型中土工格栅的刚度将是模型中土工格栅刚度的16倍(相似关系为1/4)和4倍(相似关系为1/2)。
1.5 面 板
美国联邦公路管理局(FHWA)[27]认为面板只是在回填土压实中发挥固定隔板和保护颗粒填料不受外界分化的作用,不是土工合成加筋土一体化桥梁体系的结构构件。同时,参考Guler等的试验结果可知,模块的尺寸不影响墙体实测的最大加速度结果。因此,模型中采用的模块尺寸分别为0.25 m(L)×0.15 m(W)×0.15 m(H)和0.125 m(L)×0.15 m(W)×0.15 m(H),如图3所示。土工格栅与模块通过塑料卡扣进行连接,如图4所示。
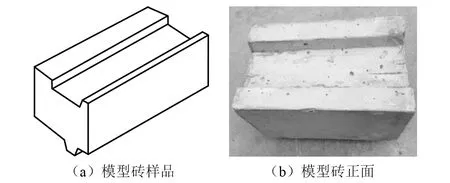
图3 模型砌块Fig.3 Modular block

图4 土工格栅和模块连接Fig.4 The connection between geogrid and block
1.6 仪器布设
图5为试验模型的仪器布设图。为测量模型的动力特性和加速度响应,在模型中安装了13个加速度计。其中,6个加速度计布设在加筋区、6个加速度计布设在回填区和一个加速度计布设在墙面板顶部,用于采集不同位置处的加速度时程。另外,在模型箱上附加两个加速度传感器用于记录输入加速度。

图5 模型设计图 (mm)Fig.5 Model design (mm)
1.7 输入地震动
模型试验采用2条地震波:①2008年汶川地震时卧龙台记录的卧龙波(WL);②1940年美国Imperial Valley 地震中El-Centro地震台记录的地震波(EL)。试验中输入归一化处理后的单向地震动。归一化和进行缩尺后的加速度时程和傅里叶谱,如图6所示。
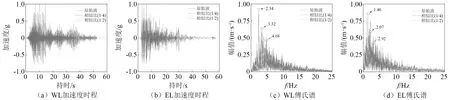
图6 输入地震动Fig.6 Input motions
为了获取模型的动力特性变化规律,在每次加速度幅值变化前后均输入白噪声(white noise,WN)。虽然持续的加载改变了模型的初始状态,但可以从模型中获取更多的信息,这与许多振动台试验采用的地震加载类型相似[28]。加载工况如表2所示。
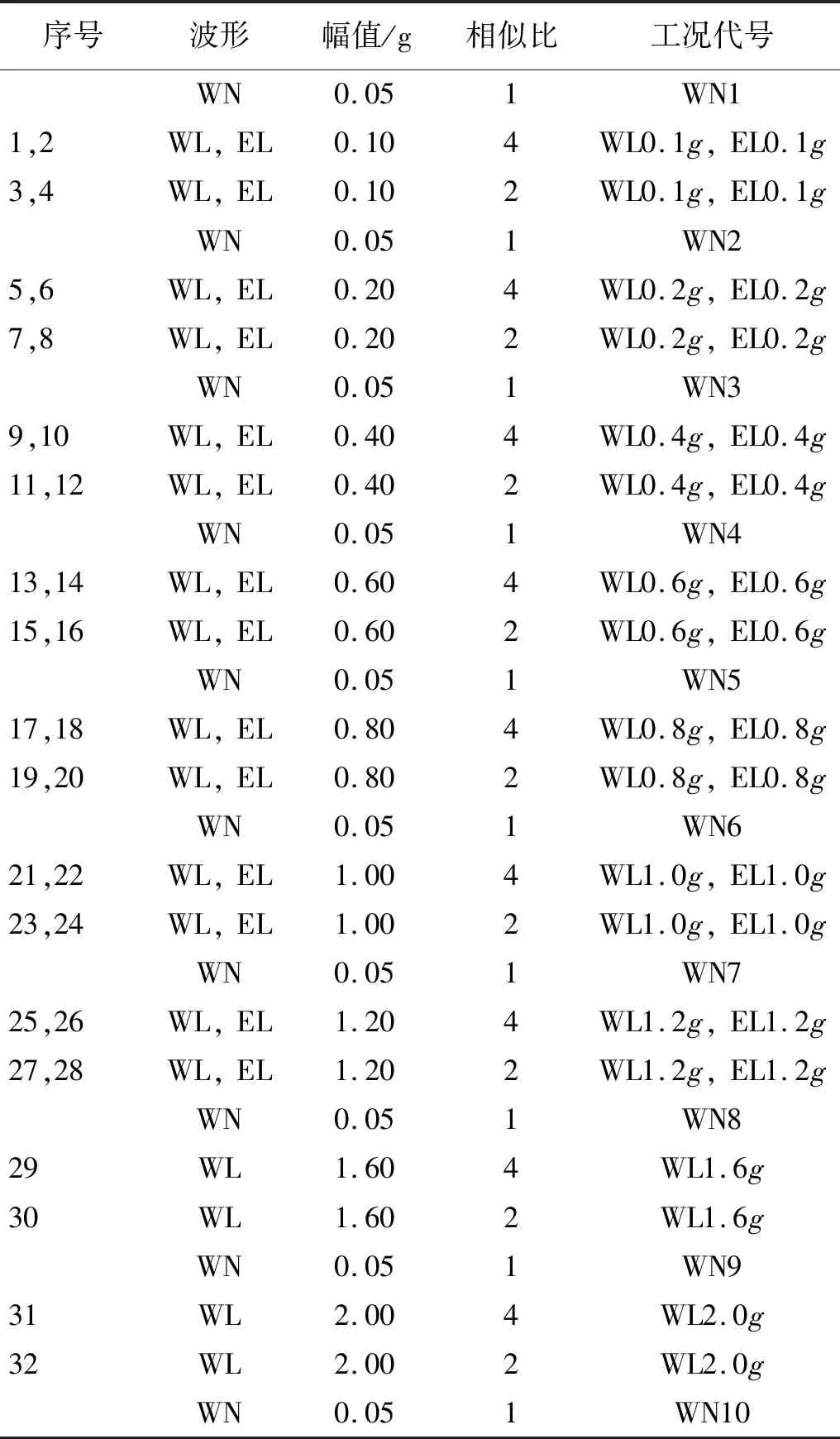
表2 加载工况Tab.2 Loading cases
2 结 果
2.1 试验现象
由于地形条件、工程用途等因素,部分位置的加筋土挡墙工程与涵洞工程相连接,这种情况在中国的铁路工程中十分常见,例如图7所示的荣成高铁站。两种结构的构造方式和整体刚度不同,导致加筋土挡墙结构面板位移分布规律和回填土沉降分布规律在刚度突变处和挡墙内部有所不同。为分析刚度突变处加筋土挡墙的面板位移和回填土沉降规律,在模型制作时,竖向每隔15 cm铺设0.5 cm厚的蓝色砂子,用于记录不同高度处的回填土沉降规律。同时,在试验开始前和每个工况结束后,均在有机玻璃上记录面板和回填土的位置,如图8所示。

图7 荣成高铁站Fig.7 Rongcheng high-speed railway station

图8 面板位移和回填土沉降记录Fig.8 Records of panel location and backfill settlement
由于试验工况众多,记录数据量大,仅列出不同工况下顶部蓝砂沉降曲线及墙面变形曲线,如图9所示。
由图9(a)可知,挡墙侧面变形分为3个阶段:①在1~3工况时,挡墙下部基本无变化,顶部两层模型砖向土体内部方向运动挤压回填土,其位移值较小;②在4~16工况时,挡墙变形模式发展为背离土体的鼓胀模式,其最大位置出现在挡墙0.5H~0.6H高度处;③在17~32工况,变形模式由鼓胀逐渐转为外倾模式:17~18工况时,挡墙中上部(0.5H~1.0H)的位移相差无几,19~32工况时,挡墙最大位移由中部(0.5H~0.6H)转移至顶部,第32工况时位移过大致使模型砖掉落挡墙破坏。
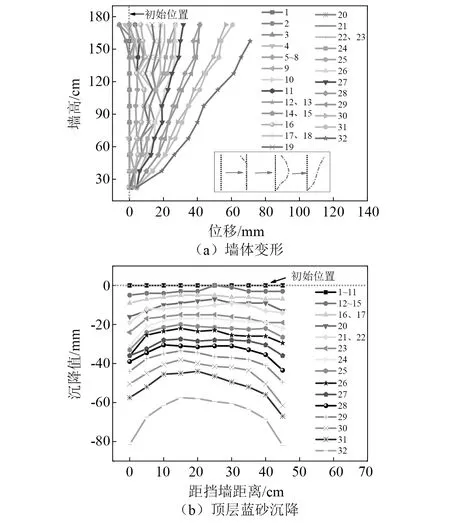
图9 试验观测Fig.9 Experimental observations
观图9(b)可确定顶部沉降趋势可分为3个阶段:①在1~11工况时,沉降基本观测不到,原因是挡墙顶部变形较小和筋材的承托作用引起;②在12~17工况时,沉降出现,各位置沉降基本均匀一致,推测是挡墙变形模式为鼓胀致使顶部位移较小,土体变形均匀;③在18~32工况时,差异沉降出现,且呈现“靠近挡墙和远离挡墙位置的两端沉降大,中间部位沉降小”的凸面趋势:在18~27工况时靠近挡墙顶部的模型砖位置沉降最大,而28~32工况时远离模型砖位置沉降最大,其原因是挡墙顶部模型位移增大和侧面挤压有机玻璃引起。
2.2 动力特性
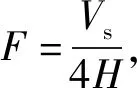
对于动力特性求解的计算理论主要有频域识别方法和时域识别方法两种:①频域方法主要通过频响函数(亦称传递函数)来反应,频响函数是互功率谱密度函数与自功率谱密度函数之商,自/互功率谱密度函数则是自/互相关函数通过韦尔奇方法(也称平均周期图方法)转换得来;②时域方法则是先通过随机减量法对输入数据进行预处理,随后采用最小二乘法、Ibrahim时域识别方法(the Ibrahim time domain technique,ITD)和节时时域方法(spare time domain technique,STD)等进行动力特性识别。本节采用时域识别方法进行自振频率和阻尼比计算。
不同阶段下模块式挡墙的一阶自振频率和阻尼比,如表3所示。由表3数据可知:(1)顶部模型砖(U-Wall)处所得自振频率与加筋区土体内(A2、A4、A6、A8、A10、A12)及振动台台面(Base)处自振频率基本一致,这与魏明等试验结果一致;对比不同加载阶段,自振频率数值在22.10~22.92 Hz,整体较一致。(2)阻尼比随着墙高的升高而减小,出现这一现象的原因是土体的剪应变随着埋深增加而逐渐增大导致[31](见式(1)和式(2)
(1)
推导得
(2)
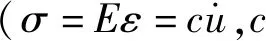
将加筋结构内(A2、A4、A6、A8、A10、A12、U-Wall)各测点的自振频率及阻尼比取平均值,作为模块式挡墙的自振频率和阻尼比。图10为模块式挡墙在不同加载阶段的自振频率和阻尼比变化规律。由图10可知:①自振频率在不同加载阶段相对稳定,幅值在22.43~22.56 Hz变化,整体幅值处于Richardson和Lee方法的预测区间内,且与伍永胜方法计算值接近;②阻尼比呈现上升或下降的非线性分布,整体区间在3.21%~4.48%,振动后各阶段的阻尼比略大于振动前的数值;③综合自振频率和阻尼比的分布可知,在多次振动(最大达到1.0g)后,模型结构并未出现大范围损伤。
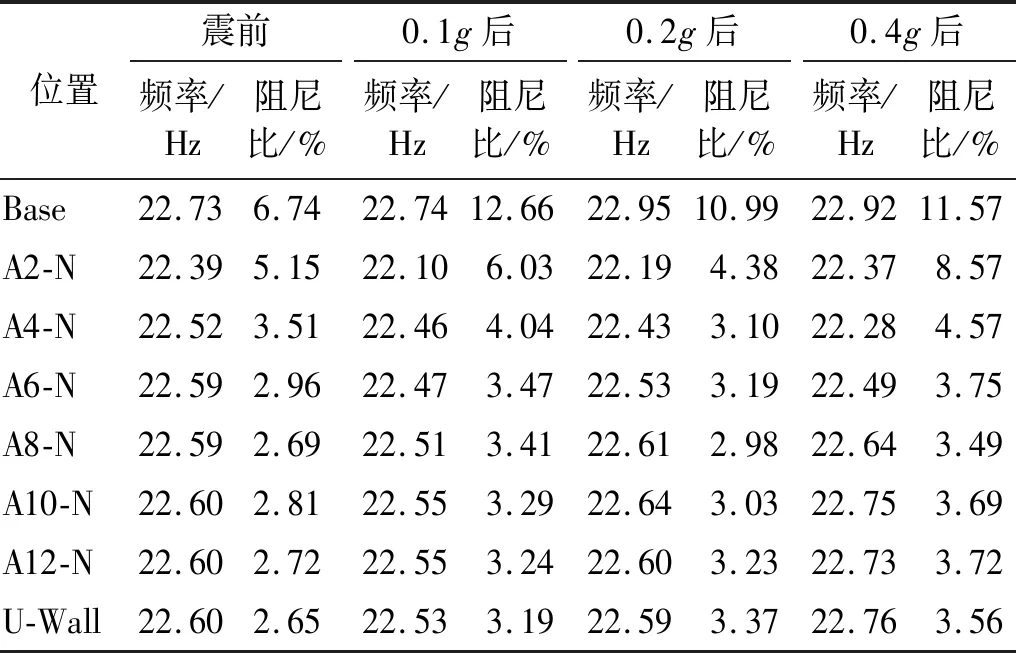
表3 模块式挡墙动力特性Tab.3 Dynamic characteristics of modular-block RSRW

图10 自振频率和阻尼比分布Fig.10 Natural frequency and damping ratio distribution
2.3 加速度响应
采用均方根方程(root mean square,RMS)对加速度时程进行处理,将挡墙内部的加速度数据与台面的加速度数据进行对比,得到不同工况下加速度放大系数的分布规律。对于加速度放大系数的取值,不同行业有不同的规定:GB 50111—2006《铁路工程抗震设计规范》(铁路规范)将挡土墙(高度小于12 m)的放大系数定义为常数1;JTG B02—2013《公路工程抗震规范》(公路规范)将放大系数归纳为折线型,如式(3)所示
(3)
式中:H为挡墙墙高;hi为墙趾到第i节的高度。
加速度放大系数在加筋区沿墙高分布规律,如图11所示。由图11可知,加筋土结构加筋区地震反应在不同试验条件(相似比、地震动)下均被放大,并不是铁路规范(H<12 m)规定的放大常数1。放大系数随墙高呈非线性变化,在结构顶部达到最大值。这是由于顶部的质量和约束均较小,导致在地震过程中形成较大的加速度和位移,与高层建筑中的鞭梢效应一致。各工况下的加速度放大趋势相似,放大系数随着峰值加速度的增大而略有起伏和降低,这一结论与Yazdandoust的试验结果一致。

图11 加速度放大系数Fig.11 Acceleration amplification factor
对比公路规范中的放大系数,可知0.6H下放大系数小于试验值,顶部大于试验结果。相似比1∶4时,WL波和EL波放大系数最大值范围分别是1.58~1.71和1.45~1.64;相似比1∶2时,WL波和EL波放大系数最大值范围是1.47~1.57和1.41~1.52。对比不同相似比下的放大系数,表明相似比对放大系数有一定影响,地震动持时长则放大系数变小。
试验结果与公路规范中的放大系数相比,0.6H处的放大系数小于试验值,墙顶大于试验结果。即试验结果与规范值存在一定误差,需要进行修正。对于实际工程,在有条件进行大型振动台试验时,可根据实测结果计算设计值。如果没有条件进行试验,可根据相似模型试验结果采用类比法进行计算。根据振动台实测结果,归纳了模块式加筋土挡墙的加速度放大分部公式,见式(4)所示
(4)
式中:H为挡墙墙高;hi为墙趾到第i节的高度。
3 讨 论
在振动台测试系统中,刚性箱与加筋土挡墙模型作为一个结合体,其动力特性可能相互影响。作者曾测试过刚性箱的自振频率,其值远大于22 Hz;同时,测试方法与Huang采用的测试手段一致;且采用傅里叶变化方法所得自振频率与时域方法计算结果基本一致。综上,可确定测试结果(自振频率和阻尼比)主要是加筋土挡墙模型自身的特性。
在加筋土挡墙的振动台试验中,筋材最大应变(0.18%)远小于筋材的破坏极限,因此,筋材的破坏情况并未在试验设计时进行考虑。已有研究表明,筋材网孔尺寸对加筋结构的承载和变形特性有较大影响[32-33],在下一步的研究还需关注。
4 结 论
(1) 在加筋土挡墙与刚性箱接触处(即刚度突变处),挡墙在不同工况下表型出不同的变形模式:挡墙顶部挤压回填土、挡墙中部鼓胀,发展至整体向临空面倾斜。顶部蓝砂分布逐渐由均布沉降发展为“两端大中间小”的凸起分布。
(2) 模型不同位置处测得的自振频率基本相同。自振频率的幅值在不同工况下比较稳定(输入达1.0g),在Richardson 和Lee方法的预测范围内,与伍永胜方法的计算值接近。阻尼比随墙高的增加而减小,且振动后阻尼比大于振动前阻尼比。
(3) 加速度放大规律呈现非线性分布,最大值出现在模型顶部。铁路规范和公路规范对加速度放大系数的定义与实测结果存在一定差距。因此,本文结合公路规范和试验结果,提出了适用于模块式加筋土挡墙的加速度放大系数分布公式。
