基于径向基函数代理模型的M形杆刚度优化

杨慧,范硕硕,王岩,刘荣强,肖洪

(1.燕山大学 机械工程学院,秦皇岛 066044; 2.安徽大学 电气工程与自动化学院,合肥 230601;3.哈尔滨工业大学 机器人技术与系统国家重点实验室,哈尔滨 150001)

可展开薄壁超弹性杆件能够利用自身弯曲存储的弹性势能实现展开,在薄膜天线、太阳帆和阻力帆中广泛使用,常见的几种不同截面的薄壁杆件有豆荚杆[1-3]、TRAC[4-5]杆和圆形储能伸缩杆(STEM)[6-7]。

Mallikarachchi等研究了带弹簧和复合材料薄壁杆的缠绕[8-9]及2层织层板在小应变下的微观力学行为[10]。楚中毅等[11-12]提出了一种用于航天探测器的主动-被动复合驱动可展开豆荚杆,在模态和缠绕分析的基础上对豆荚杆参数进行了优化设计。文献[13-15]分析了可展开复合材料薄壁杆的压扁和缠绕过程的实验和数值。Bessa等[16-17]采用数据驱动法对TRAC杆进行了优化设计,但忽略了2个带弹簧之间的黏结段影响。Roybal等[18]发现在相同的压扁截面高度时,TRAC杆的截面惯性量是豆荚杆的10倍,是STEM的34倍。杨慧等[19]提出了一种N形超弹性杆,并对其后屈曲性能进行了优化。目前,对超弹性杆压扁和缠绕过程的力学性能进行的研究较多,对完全展开状态下的承载能力却很少研究。

本文以M形超弹性杆(简称M形杆)为研究对象,对展开状态下的M形杆进行了刚度分析和几何参数优化,从而提高M形杆展开状态的刚度。首先,利用有限元软件ABAQUS建立M形杆绕x、y和z轴弯曲、扭转,以及沿z轴压缩的有限元模型;然后,提取绕x轴弯曲刚度EIx(h,θ2)、绕y轴弯曲刚度EIy(h,θ2)、绕z轴扭转刚度GJz(h,θ2)、沿z轴压缩刚度EAz(h,θ2),采用径向基函数(radial basis function,RBF)法建立代理模型;最后,以上述4种刚度为目标,以质量为约束,以黏结段长度h和内侧带簧片圆心角θ2为变量,采用粒子群(particle swarm optimization,PSO)算法进行优化。

1 M形杆几何模型

M形杆截面几何尺寸如图1所示。M形杆横截面被压扁之后可以绕轮毂缠绕,缠绕弯曲过程中存储应变能,释放约束之后,依靠存储的弹性势能,能够展开到初始状态。M形杆是由4个带簧片组成,2个外带簧片只有1个黏结段,2个内带簧片有中心对称的2个黏结段,黏结段的长度为h。内侧带簧片由2个圆角外切弧组成,M形杆4个带簧片有2个独立的参数,即h和θ2。由压扁后内外侧宽度相同可以推导出如下关系:

由图1可以得到M形杆质量M0为

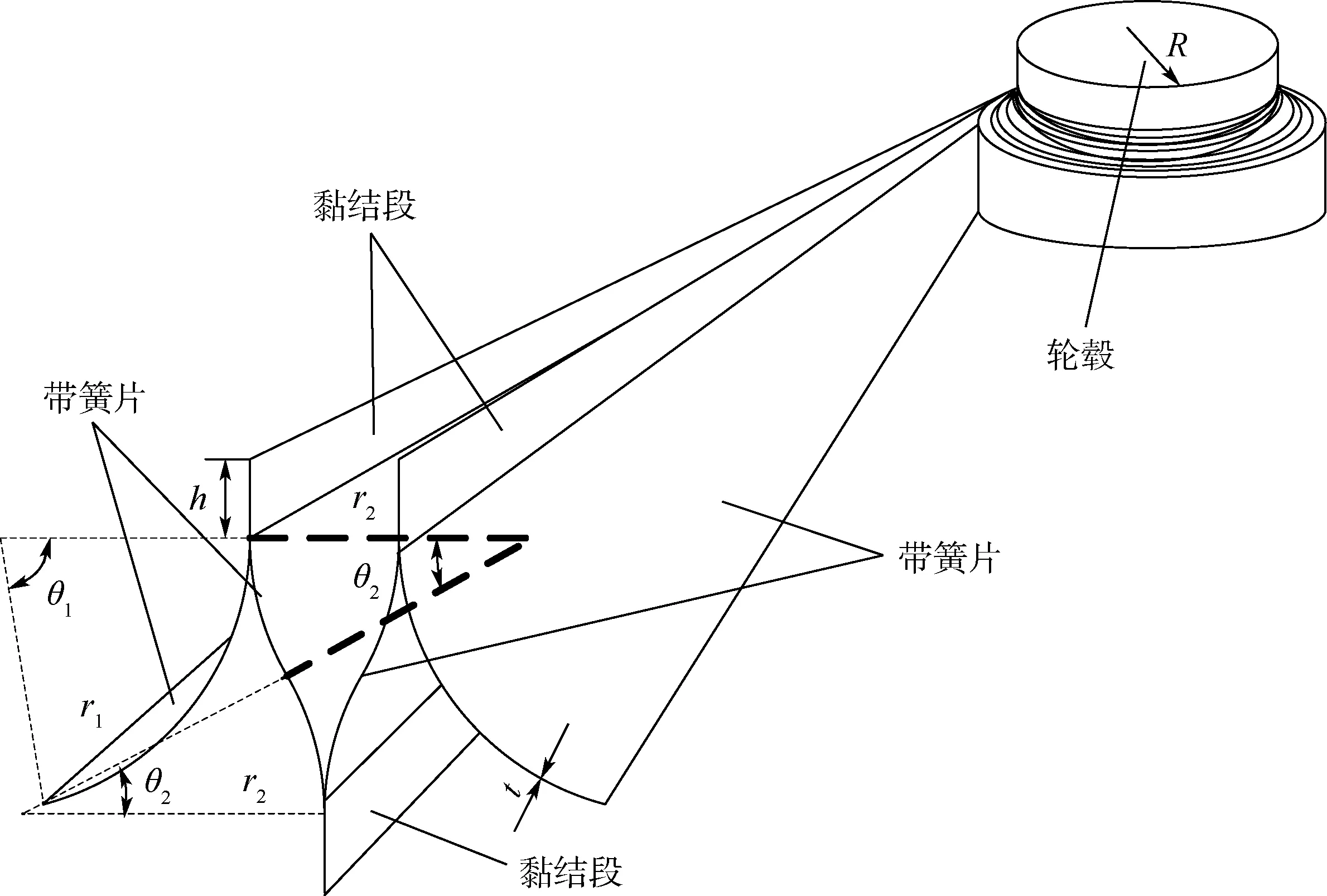
图1 M形杆缠绕几何示意图Fig.1 Geometric schematic diagram of M boom coiling

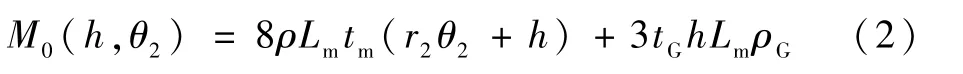
式中:杆件长度Lm=0.4m;厚度tm=0.15mm不变;ρ为复合材料T800的密度;tG为黏结胶厚度;ρG为黏结胶密度。

2 有限元建模分析

M形杆的仿真模型以实际工况为依据,采用4层复合材料的铺设方式,复合材料叠加顺序为[45°/-45°/-45°/45°],每 层 的 厚 度 为t=3.75×10-5m,复合材料属性如表1所示,铺层方式如图2所示。

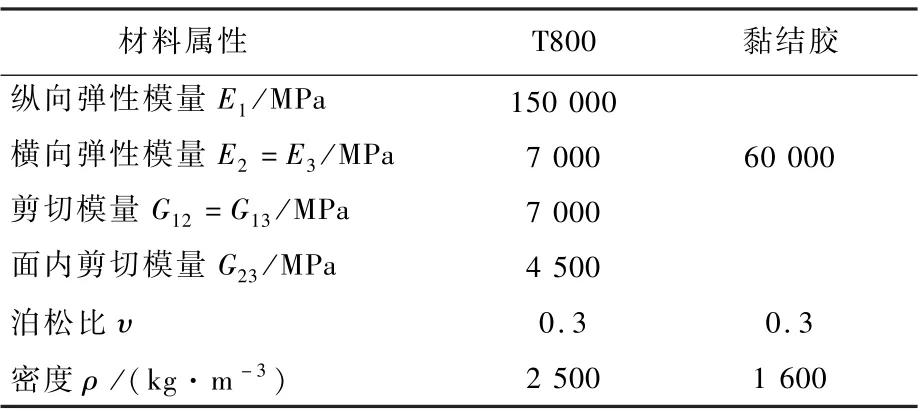
表1 T800材料属性Table1 Material properties of T800

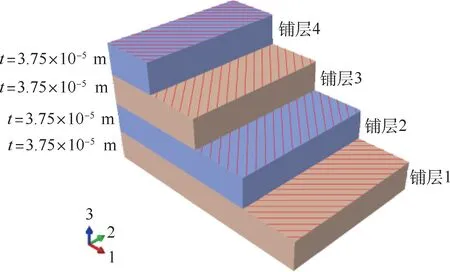
图2 M形杆各层材料铺设布置图Fig.2 Material laying layout of each layer of M boom

创建一个Cohesive部件模拟M形杆黏结段,M形杆和黏结胶分别采用壳单元S4R和表面单元C3D8R模拟,由于M形杆的横截面关于y轴对称,只需对相互对称的一侧参数进行研究。为了得到黏结段长度h和内侧带簧片圆心角θ2对M形杆临界载荷的影响,在M形杆两端的横截面处设置2个参考点RP1和RP2,并以2个参考点为控制点与杆件两端建立MPC约束,如图3所示。固定参考点RP1,且限制参考点RP2的5个自由度,给RP2施加一定的旋转或平移自由度,UX、UY、UZ分别为沿x、y、z轴水平位移,RX、RY、RZ分别为绕x、y、z轴旋转位移,具体施加载荷情况如表2所示。

结合表2和图3,M形杆绕x轴弯曲刚度EIx(h,θ2)、绕y轴弯曲刚度EIy(h,θ2)、绕z轴扭转刚度GJz(h,θ2)、沿z轴压缩刚度EAz(h,θ2)可表示为

图3 M形杆有限元模型Fig.3 Finite element model of M boom

表2 参考点RP2在不同情况下的边界条件Table2 Reference point RP2boundary conditions under different conditions

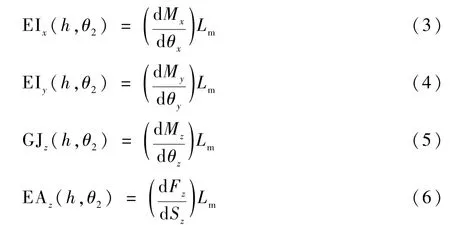
式中:Mx、My、Mz分别为绕x、y、z轴的力矩;θx、θy、θz分别为绕x、y、z轴旋转的角度;Fz为轴向力;Sz为压缩位移。

当h=7mm,θ2=24°,θ1=68.06°时,M形杆绕x、y轴弯曲的应力云图和力矩曲线如图4和图5所示,绕z轴扭转的应力云图和力矩曲线如图6所示,沿z轴压缩的应力云图和反作用力曲线如图7所示,图中的圆圈标记点为M形杆的临界载荷点。

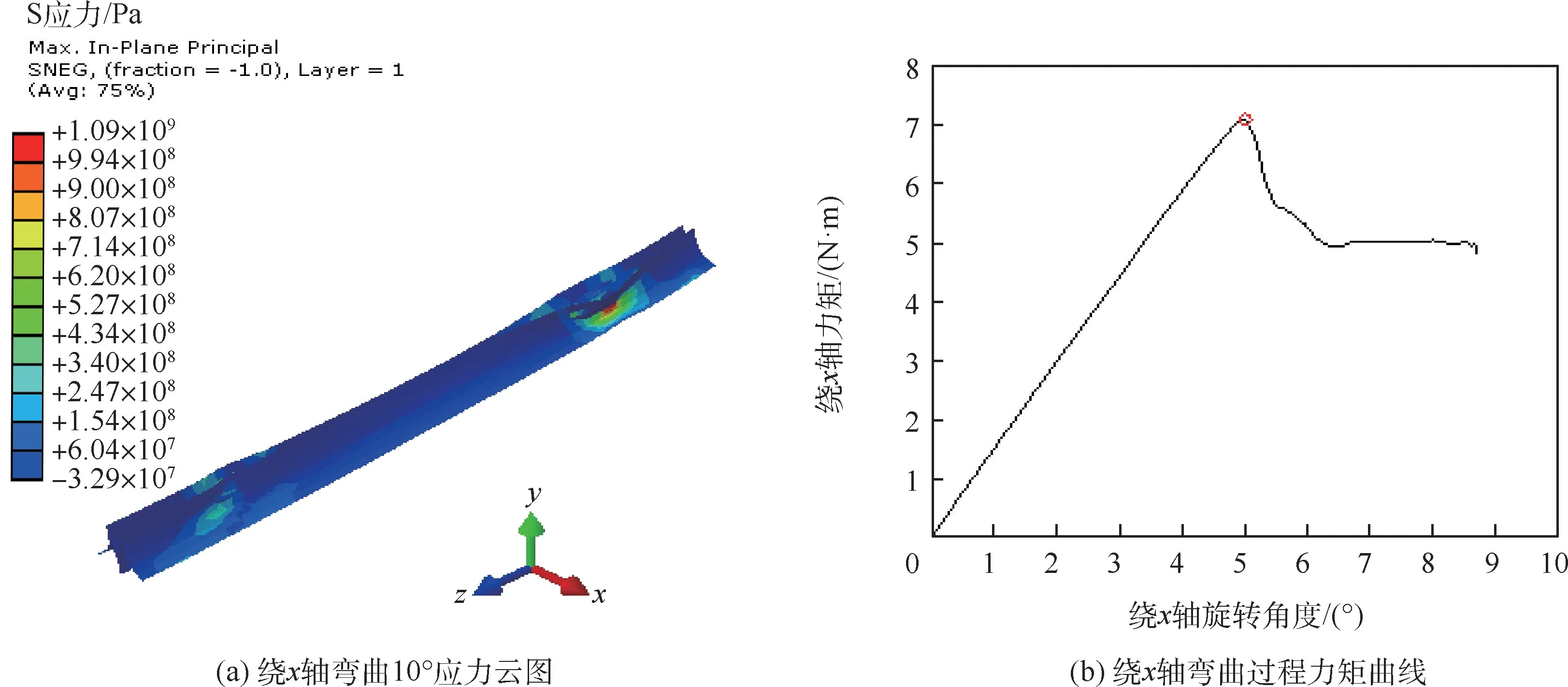
图4 M形杆绕x轴弯曲的应力云图和力矩曲线Fig.4 Cloud chart of stress and bending moment curve of M boom around x-axis

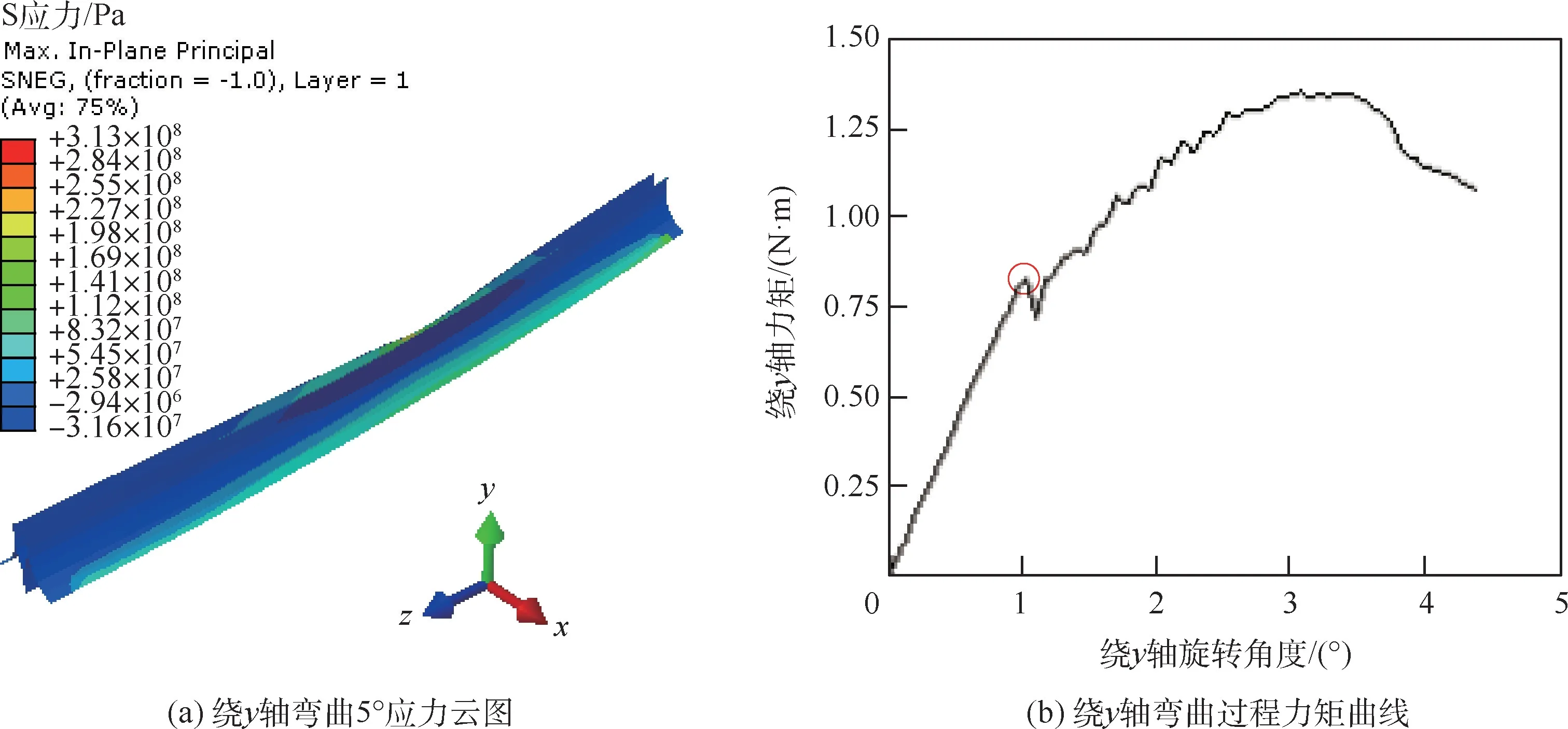
图5 M形杆绕y轴弯曲的应力云图和力矩曲线Fig.5 Cloud chart of stress and bending moment curve of M boom around y-axis

图7 M形杆沿z轴压缩的应力云图和反作用力曲线Fig.7 Stress cloud diagram and reaction force curves of M boom compressed along z-axis

为了得到最优刚度下的h和θ2组合,需要在样本空间中进行大量的有限元数值模拟计算。共在样本空间中生成3000个样本点,每个样本点在Intel(R)Core(TM)i5-9400F CPU@2.90GHz 6核配置计算机上仿真计算得到4种刚度需要约40min,为了节约时间和资源成本,需要构建代理模型,代理模型完成后利用MATLAB可以在1s左右计算出4种刚度输出数值。代理模型简单来说是通过已有样本点构建输入变量与输出目标之间的映射关系,从而利用映射关系来近似预测样本空间中其他未知样本点的输出值。为了构建关于4种刚度EIx、EIy、GJz、EAz的代理模型,采用全因子法进行实验设计。h取值范围为5～10mm,以1mm等间隔,共有5,6,7,8,9,10六水平,θ2取值范围为22°～26°,以1°为等间隔,共有22,23,24,25,26五水平,共在样本空间中生成30个样本点,其有限元分析结果如表3所示,用30个已知样本点建立代理模型预测整个样本空间中3000个样本点输出值。

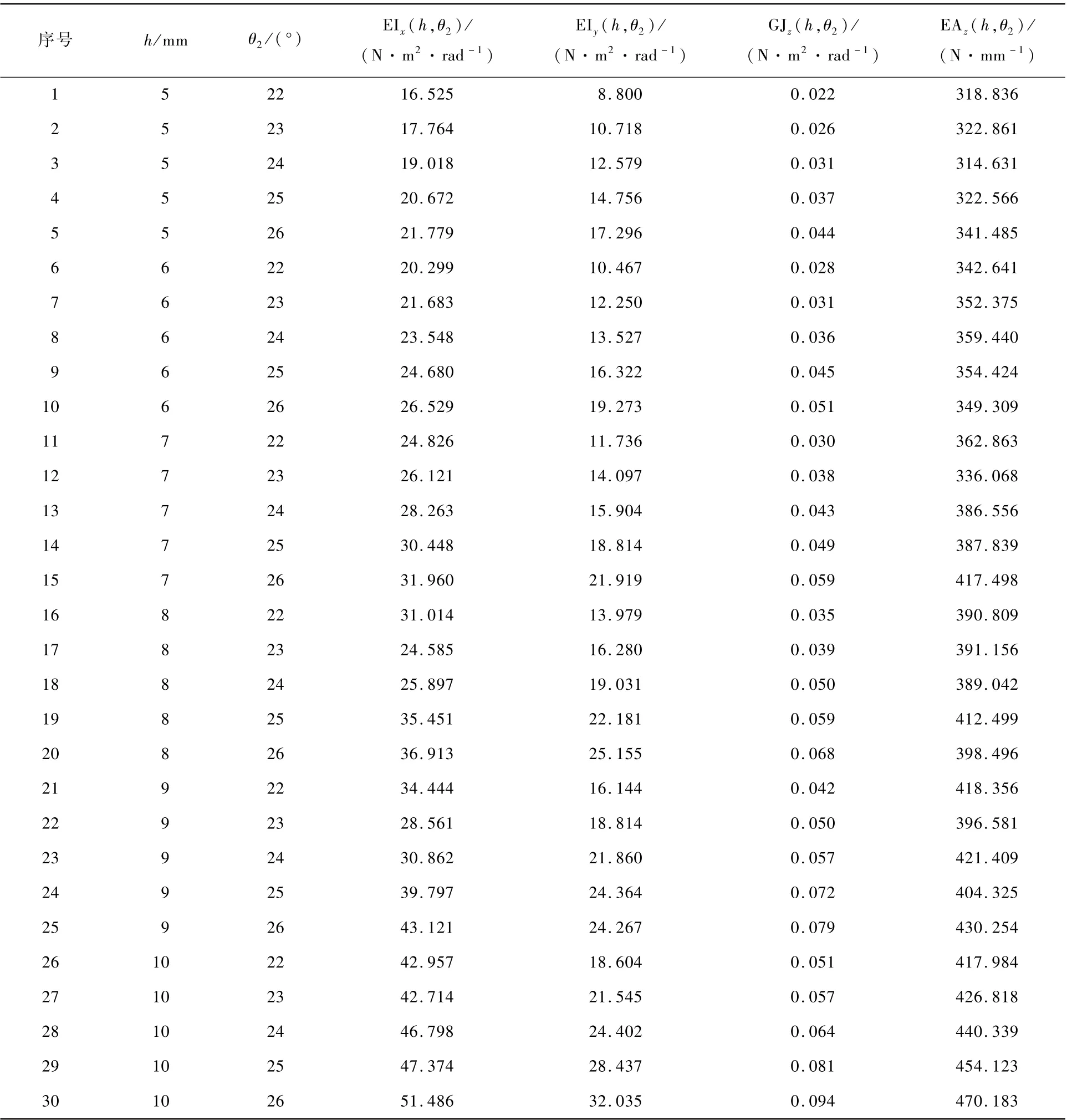
表3 样本点Table3 Sample points

3 径向基函数代理模型

3.1 建立代理模型

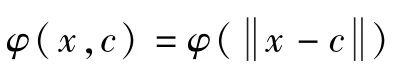
径向基函数代理模型表达式如下:

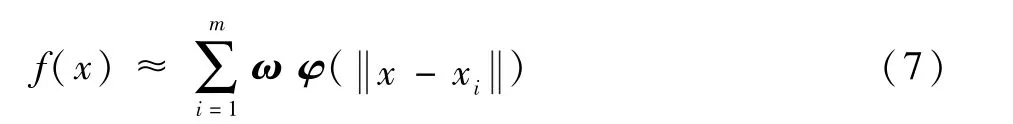
表4 径向基函数代理模型核函数中常数c的取值Table4 Values of constant c in kernel function of RBFs surrogate model

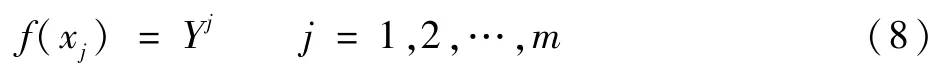
将式(8)代入式(7),可以得到

由式(10)可求出加权系数ω,代入式(7)可得到代理模型表达式,对未知点的输出值进行估算。

3.2 模型误差分析

用于建立代理模型的样本点处,其实际响应结果与代理模型的近似值相等,无法通过这些样本点衡量代理模型的精度,因此评估代理模型精度是否满足要求需要选取额外的样本点。可以定义相对误差的表达式,即

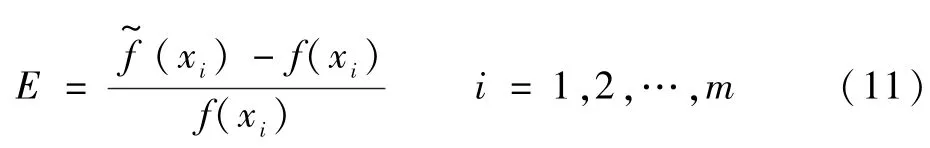
式中:f(xi)为第i个样本点处的有限元结果;(xi)为第i个样本点处的径向基函数代理模型近似结果;m为样本点个数。由检测样本点处误差大小来评估代理模型的精度和拟合效果。建立代理模型共选取样本点30个,为保证代理模型拟合精度,避免误差测试样本点的随机性导致偏差,采用交叉验证法建立代理模型,30个样本点共分为6组,每组5个样本点,每次选择其中5组建立代理模型,余下1组做为误差检测样本点,选择检验误差最小的1组模型作为最终代理模型。最终得到4个关于EIx(h,θ2)、EIy(h,θ2)、GJz(h,θ2)、EAz(h,θ2)的代理模型,测试误差结果如表5所示。模型最大相对误差的绝对值分别为6.155%、1.666%、1.518%和5.538%,代理模型精度均满足要求。

表5 误差测试样本点Table5 Sample points of relative errors

3.3 代理模型响应面

关于EIx(h,θ2)、EIy(h,θ2)、GJz(h,θ2)、EAz(h,θ2)的响应面如图8～图11所示。由响应面图形可知,黏结段长度h的变化对EIx(h,θ2)和EAz(h,θ2)有 显 著 影 响,h和θ2的 变 化 对GJz(h,θ2)和EIy(h,θ2)产生变化影响程度相当。

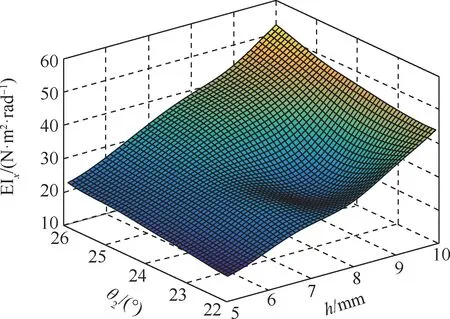
图8 EIx(h,θ2)响应面Fig.8 Response surface of EIx(h,θ2)

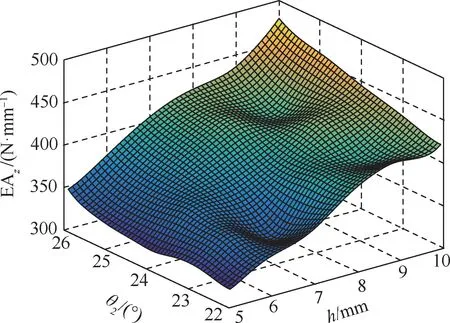
图11 EAz(h,θ2)响应面Fig.11 Response surface of EAz(h,θ2)

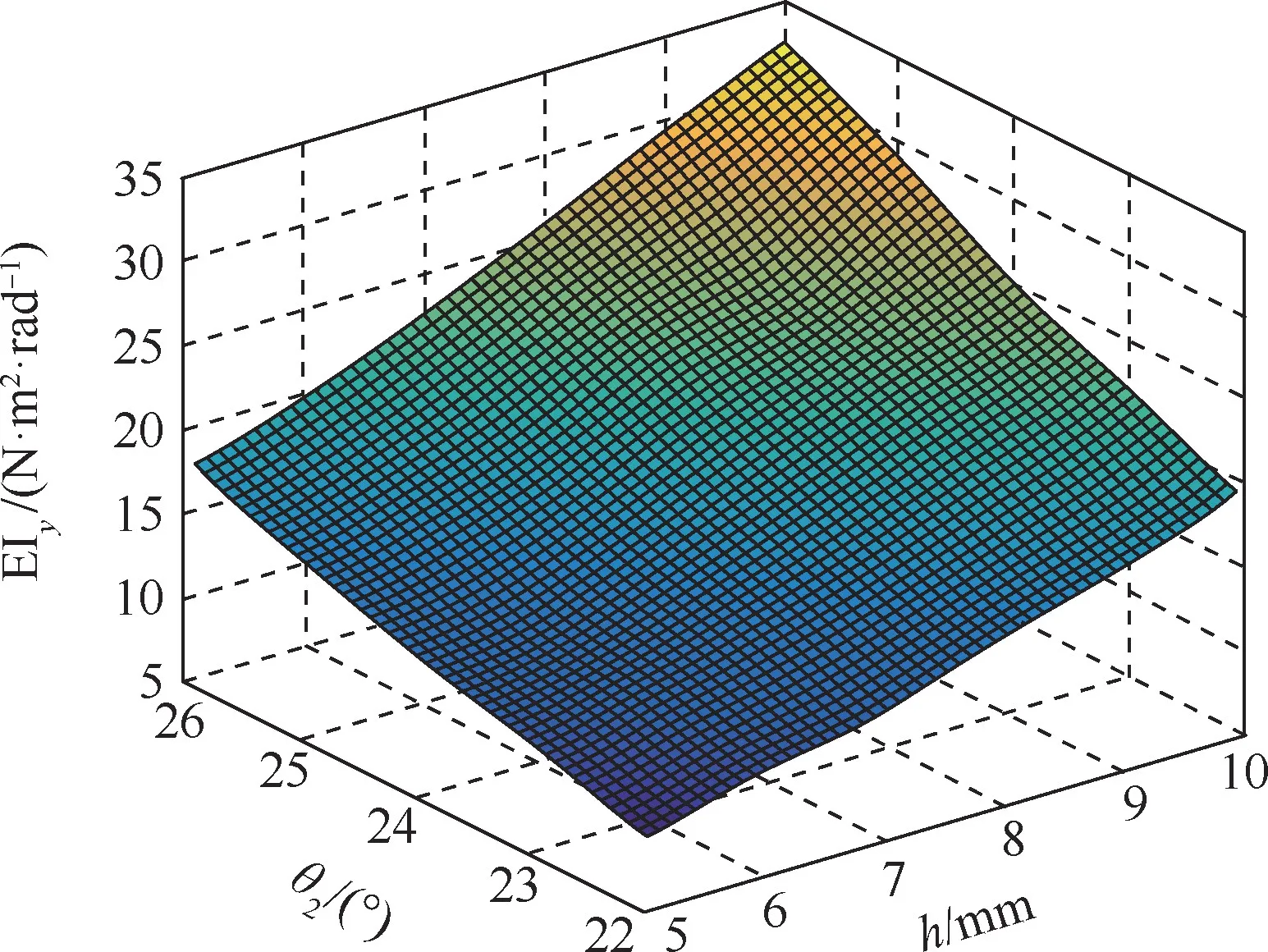
图9 EIy(h,θ2)响应面Fig.9 Response surface of EIy(h,θ2)

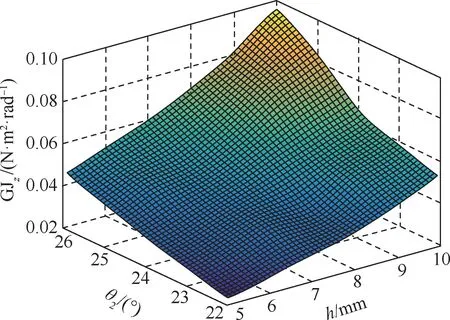
图10 GJz(h,θ2)响应面Fig.10 Response surface of GJz(h,θ2)

4 优化设计

以绕x轴弯曲刚度EIx(h,θ2)、绕y轴弯曲刚度EIy(h,θ2)、绕z轴扭转刚度GJz(h,θ2)和沿z轴压缩刚度EAz(h,θ2)为4个目标量,目标量取最大值,以黏结段长度h和内侧带簧片圆心角θ2为设计变量,以质量为约束,优化设计如式(12)所示。用粒子群算法进行多目标优化,最大迭代次数设为100,粒子群数量设为30,惯性权重、群体学习因子及自我学习因子均设为0.9。如式(13)所示,目标函数O值的计算为所有优化目标分量Xi和对应第i个目标分量的权重因子Wi、比例因子Si加权之和。如果目标分量的比例因子和权重相等,目标分量数量级较大的对优化结果影响较大,比例因子和权重的设置是为了调整在优化过程中各子目标的重要程度。为方便计算,比例因子统一设置为1。由于M形杆为开口型超弹性杆,扭转刚度GJz较小,对杆件整体刚度影响较大,在优化中赋予较大权重,设为1000;EIx、EIy、EAz、M0根据自身数量级的大小,分别设置为1.2、2、0.1、1.5。4个目标量及约束量M0的比例因子和权重如表6所示。在多目标优化问题中,多个目标在约束条件下相互制约,找到的一般不是所有子目标的最优解,而是Pareto解,可行结果即为Pareto最优解,一般不止一个,多目标优化问题的最终解是从所有Pareto最优解中挑一个最优折中解,由于M形杆扭转刚度对杆件整体刚度影响较大,选择扭转刚度较大的一个解做为最终解。优化后的Pareto结果如表7所示。最优设计点为第2个,h=7.8945mm,θ2=26°,θ1=74.616°,结果如表8所示。

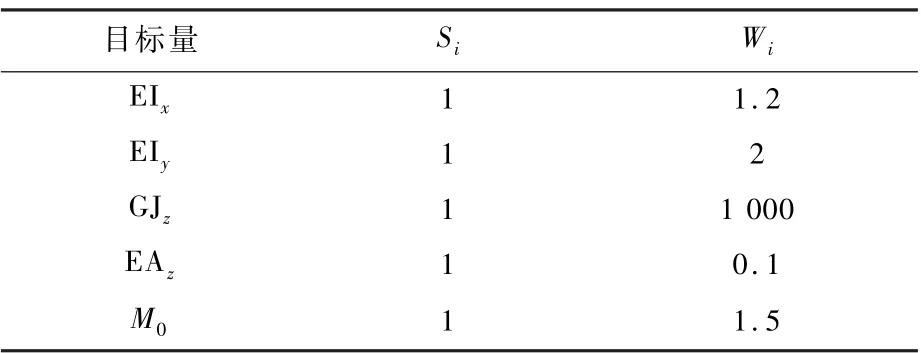
表6 目标量和约束量的比例因子和权重Table6 Scale factors and weights of objective and constraint quantities

表7 Pareto设计点Table7 Pareto points of design

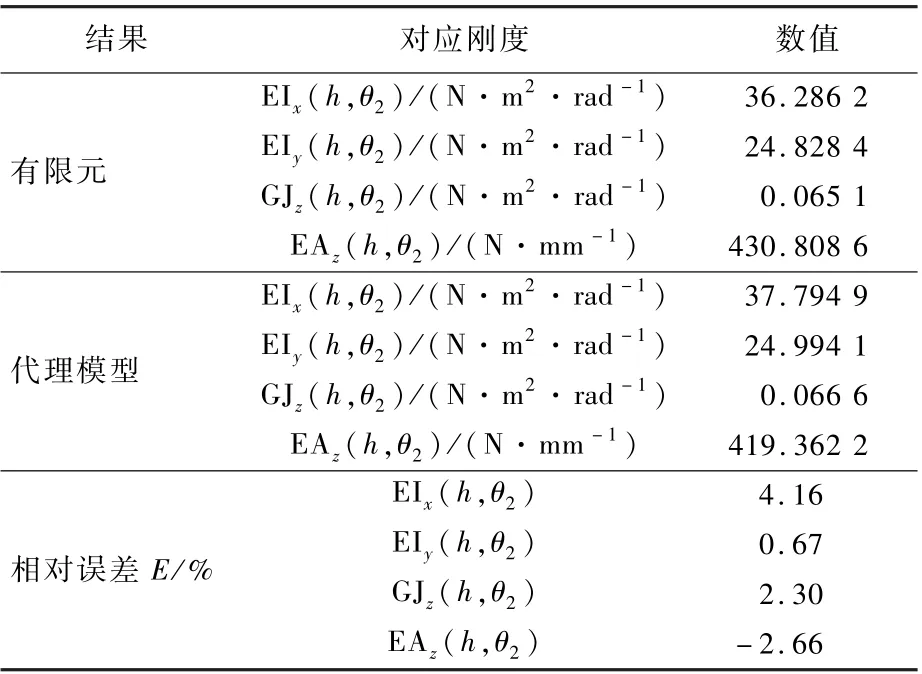
表8 最优设计点Table8 Optimal point of design

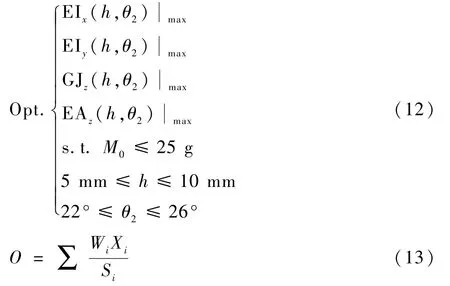
5 结 论

1)为了节省仿真分析时间,建立了径向基函数代理模型,得到4种刚度相关的4个代理模型,最大相对误差的绝对值不大于6.155%,精度均满足要求。

2)采用粒子群算法进行参数优化,得到黏结段长度h=7.8945mm,内侧带簧片圆心角θ2=26°时,有最优的弯曲刚度、扭转刚度及压缩刚度。最优点的有限元仿真结果与代理模型预测结果之间最大相对误差仅为4.16%。

3)同内侧带簧片圆心角θ2相比,黏结段长度h的变化对绕x轴弯曲刚度及沿z轴压缩刚度的变化影响显著;而h和θ2的变化对绕y轴弯曲刚度及绕z轴扭转刚度的变化影响程度较为接近。