数据立方体关联挖掘在红外抗干扰中的应用

2022-11-30吴鑫伍友利牛得清蔡宇轩徐洋陈鞭

北京航空航天大学学报 2022年11期

吴鑫,伍友利,*,牛得清,蔡宇轩,徐洋,陈鞭

(1.空军工程大学航空工程学院,西安 710038; 2.中国空气动力研究与发展中心,绵阳 621000)

在现代空战中,随着战场环境复杂化、对战目标智能化、作战空间多元化的特点,对红外空空导弹性能提出了更高、更严的要求。其中包括高隐蔽性、高效费比、灵活机动,尤其是需要拥有很强的抗干扰能力[1]。自20世纪90年代红外诱饵技术的广泛应用,红外导弹的抗干扰能力开始备受各个军事大国关注,红外导弹抗干扰能力设计和评估一直是领域内公认的一个难题[2]。

经过20几年的发展,红外抗干扰能力设计及评估方法层出不穷。胡朝晖和闫杰[3]为解决红外空空导弹抗干扰性能的定量评估,提出一种贝叶斯估计算法,但该算法依赖于先验概率,且假设的属性之间相互独立,而抗干扰性能各属性之间相关性较大,因此该算法的局限性较大;王涛和王祥[4]从作战的空、时、频、能量、信息5个维度提出一套红外抗干扰评估方法;李慎波等[5]则从导弹作战参数出发研究对红外诱饵干扰效能的影响。随着红外抗干扰能力设计的深入,红外对抗环境的量化建模也成为了研究热点,通过对场景构成和红外物理特性构建红外抗干扰要素模型,对对抗中的环境复杂度进行量化[6]。同时各种机器学习算法如随机森林、支持向量机、贝叶斯分类器等[7-9]与红外抗干扰评估的融合,产生各个算法下的评估方法。但上述方法中均未提到抗干扰指标体系中各指标与红外导弹脱靶量之间的关系,各干扰因素与脱靶量之间的强、弱耦合关系为抗干扰能力的设计及评估提供了着重点。

本文改变诱饵弹投掷参数、弹目相对态势及目标机动方式,这些参量在本文中统称为干扰量,再利用红外抗干扰仿真平台获取海量数据,建立数据立方体将数据进行预处理,最后通过数据挖掘算法得出干扰量与脱靶量之间的关联规则,根据关联规则分析出各干扰量与脱靶量之间的耦合强弱;同时为飞行员在相应态势下如何投掷诱饵,如何进行战术机动规避导弹提供辅助决策。

1 红外抗干扰数据获取

1.1 红外对抗模型构建

由于本文试验需基于大量的样本试验数据,为此需要构建红外对抗模型,其仿真流程如图1所示。从整个仿真流程来看,红外对抗模型主要包括诱饵弹、目标、导弹3个部分,其中除了解算诱饵弹、目标、导弹的运动模型外,还需要解算红外辐射模型。图中的初始参数包括:①导弹-目标初始态势信息;②诱饵投掷器信息;③目标机动信息;④各对抗实体自身属性信息,如质量、时间常数等。

图1 红外对抗仿真流程Fig.1 Simulation process of infrared countermeasure model

导弹、目标、诱饵弹的运动模型依据各自的质心运动方程与质心动力学方程建立[10],对于红外辐射模型的构建,本文采用单线组谱带模型[11]及计算流体力学的方法分别离线计算目标与诱饵的红外辐射强度。

1.2 干扰量设定

本文试验中干扰量包括诱饵投掷参数(parameters of infrared bait,PIB)、目标机动方式(target maneuvering mode,TMM)及弹目相对态势(missile and target relative position,MTRP)[12-13]。

其中PIB包括投掷总数、每次投掷个数、每组投掷个数、投掷时机、投掷组内间隔、投掷组间间隔、投掷速度、水平投掷角度、垂直投掷角度;TMM包括无机动、左转弯、右转弯、跃升;MTRP包括弹目距离和进入角。

根据实际作战态势及红外对抗模型边界条件的约束,本文制定了如表1所示的干扰量参数设定范围。结合4种目标机动方式,采用控制变量的方法,将所有的干扰量组合所形成的干扰态势遍历一遍,作为输入量导入红外对抗模型中,最终得出50000条不同态势下的脱靶量数据作为后续试验的样本集。

表1 干扰量参数设定范围Table1 Range of disturbance variable parameters

2 基于数据立方体的数据预处理

2.1 构建数据立方体

定义1多维数据模型(multi-attribute data model,MDM)。将不同对抗态势下多维数据进行记录,可将其表达为MDM=(F0;F1;…;Fi;M),其中Fi为数据的维度,M为维度度量。以红外导弹抗干扰过程为例,红外对抗的多维数据模型可以表示为MDM=(诱饵投掷参数;弹目相对态势;目标机动方式;脱靶量;4)。其中,PIB包含9个参量,可表示为:PIB=(Ns,Ne,Nf,Tl,Ti,Te,Vf,θl,θv);MTRP包含2个参量,可表示为:MTRP=(θm,Dr);TMM为1-无机动、2-左转弯、3-右转弯、4-跃升;将脱靶量(miss distance,MD)分为3个等级:MD1＜12m为摧毁、严重毁伤(目标解体或丧失飞行能力);12m≤MD2＜16m为中度毁伤(目标失去作战能力但还能飞行);MD3≥16m为轻微毁伤、逃逸成功。

例如,MDM=(24,2,6,1,0.2,0.8,20,30,60;70,3.5;4;MD1)可解析为:目标携带红外诱饵弹24枚,投掷分为3组每组6枚,每次投掷2枚,当仿真经过1s后开始投掷,1个大组中组内投掷间隔为0.2s,组与组之间的投掷间隔为0.8s,诱饵的投掷速度为20m/s,投掷方向与机体横轴(x轴)夹角为30°、机体纵轴(y轴)夹角为60°;弹目相对态势的初始距离为3.5km,导弹进入角为70°,此时目标采取跃升机动对导弹进行规避,最后脱靶量为MD1级,说明在此红外对抗仿真作战态势下,目标逃逸失败。

定义2数据立方体(data cube,DC)。数据立方体是由数据的维和事实定义的,允许对多维数据进行建模和观察。对于不同红外对抗态势下的仿真结果,按照不同维度中参量的组合构建一个数据集合。按照多维数据模型的集合,所构成的数据立方体有4个维度:PIB、MTRP、TMM、MD。

通过4个维度构成的分组总数,可能的分组是{(PIB,MTRP,TMM,MD),(PIB,MTRP,TMM),(MTRP,TMM,MD),(PIB,MTRP,MD),(PIB,TMM,MD),(PIB,MTRP),(MTRP,TMM),(TMM,MD),(PIB,TMM),(PIB,MD),(MTRP,MD),(PIB),(MTRP),(TMM),(MD),(all)},其中(all)指不对任何数据分组,即不进行分维的原始数据。这些分组形成了数据立方体的方体格,如图2所示。

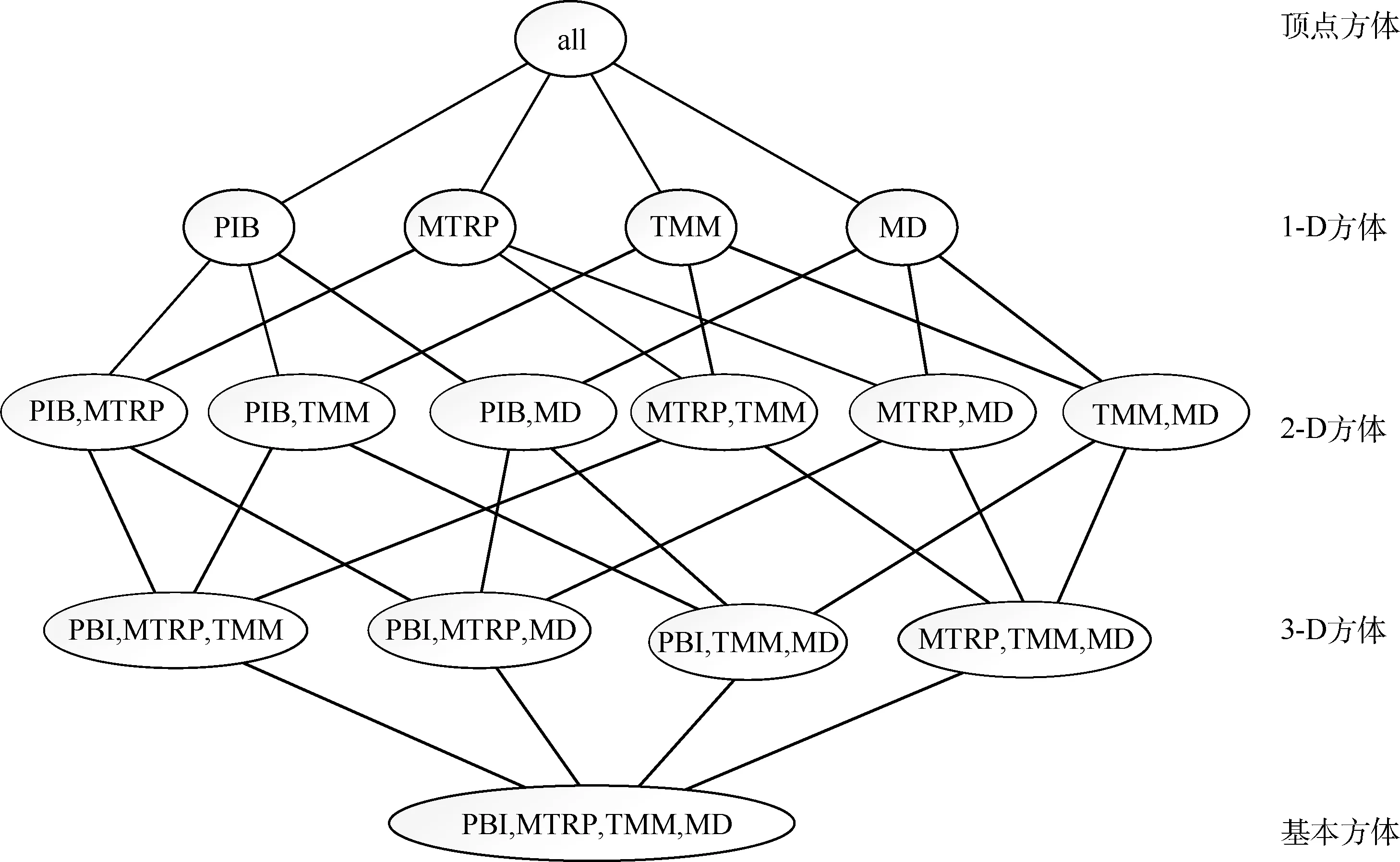
图2 四维数据立方体Fig.2 Four-dimensional data cube

其中基本方体包含PIB、MTRP、TMM、MD这4个维,是低泛化(最特殊化)的方体,该方体中每一条由此四维组成的数据就是红外对抗模型输入量与输出量。顶点方体是最高泛化(最不特殊化)的方体,包含红外对抗模型运行后的所有数据。如果从顶点开始,沿方体的格向下探查,这等价于在数据立方体中下钻;如果从基本方体向上探查,则类似于上卷。通过对数据立方体下钻、上卷等方式,对方体中的数据类型及数据模式进行预处理。

通过图2观察四维数据立方体的数据变得有点麻烦,因此通过降维的手段,把基本方体转换成3-D方体序列。

2.2 数据立方体的降维

由于四维的立方体数据不好进行观察和处理,本文选用MD作为固定维,将MD按3个等级(MD1、MD2、MD3)把数据分为三大类,这样就可将基本方体转化为3个3-D方体,3-D方体的3个维度:诱饵投掷参量(P)、弹目相对态势(M)、目标机动方式(T)。降维后数据立方体示意图如图3所示。

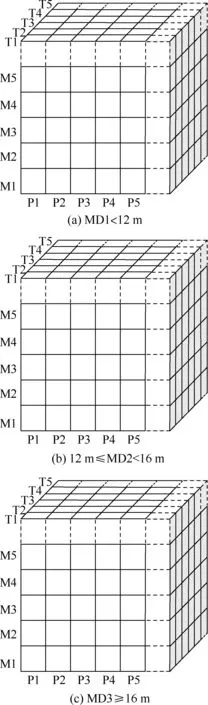
图3 按MD降维后数据立方体示意图Fig.3 Diagram of data cube after dimension reduction by MD

2.3 数据立方体的查询操作

在OLAP软件中关于对数据立方体的操作包括Cube、Roll-up及Drill-down等操作符号[14-15],通过SqlServer的操作步骤,得出降维后数据立方体各参量之间的映射关系如表2～表4所示。以MD1立方体为例,在SqlServer中关于数据立方体的具体查询步骤为

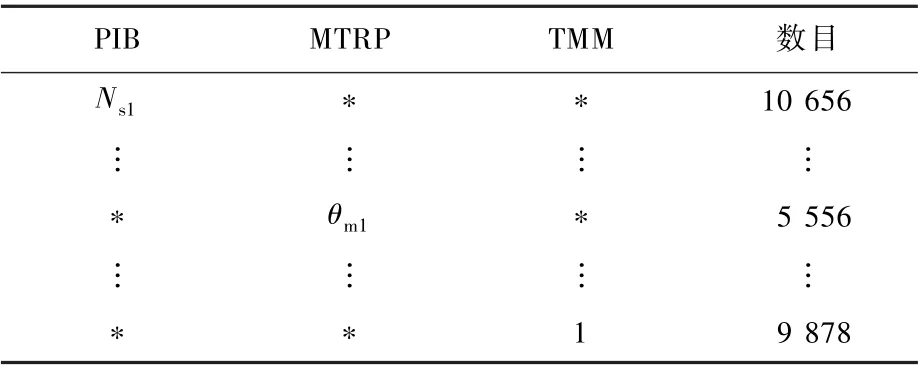
表2 MD1立方体的1-D关系Table2 1-D relation table of MD1cube

表4 MD1立方体的3-D关系Table4 3-D relation table of MD1cube

select PIB,MTRP,TMM,SUM

from MD1

group by PIB by PIB

group by MTRP by MTRP

group by TMM by TMM

该步骤可以解释为从MD1数据立方体中分别以PIB、MTRP、TMM进行分组,并且统计每一个干扰量及其组合的数目。

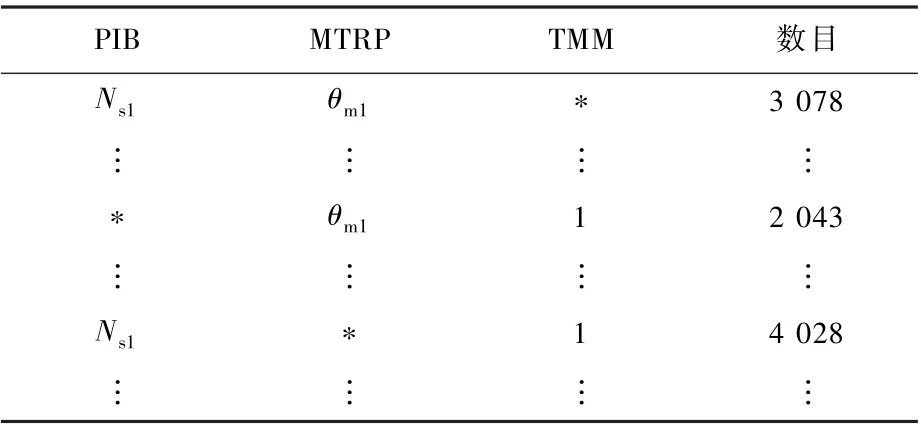
表3 MD1立方体的2-D关系Table3 2-D relation table of MD1cube

3 关联规则生成

3.1 关联规则算法相关概念

Apriori算法与FP-Growth算法是关联规则算法中的经典算法。由于Apriori算法在产生完整的频繁模式集之前需要对数据库进行多次扫描,同时产生大量的候选频繁集,这就使Apriori算法在时间和空间复杂度较大,但FP-Growth算法只需对数据库进行2次扫描,使用事物数据集的压缩来有效地产生频繁项集,因此FP-Growth算法比标准的Apriori算法要快几个数量级[16]。故选择FP-Growth算法作为本试验关联规则生成算法。

定义3关联规则(Rules)。关联规则就是形如X→Y的表达形式,其中X,Y⊆I且X∩Y=φ,I是所有项的集合。关联规则就是要找出支持度、置信度都大于等于支持度阈值与置信度阈值的所有规则。

定义4支持度(Sup)和置信度(Conf)。假设X和Y都是数据集中的事务,支持度就是确定规则可以用于给定数据集的频繁程度,而置信度确定Y在包含X的事务中出现的频繁程度。这2种度量的表示形式如下:

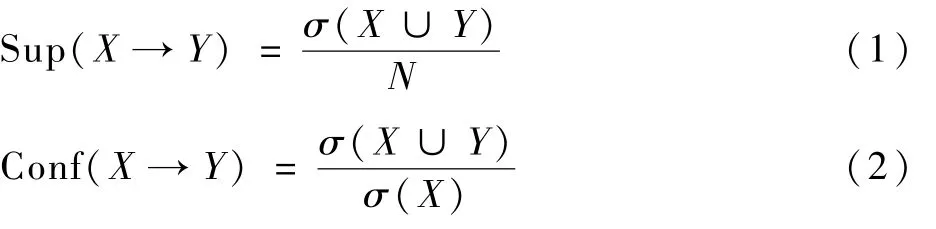
式中:σ(·)表示项集的支持度计数;N为数据集事务总数。

定义5Kulczynski度量指标(Kulc)。仅用支持度-置信度框架来衡量关联规则的好坏存在许多局限性,支持度的缺陷在于许多潜在意义的模式由于包含支持度小的项而被删去;置信度的缺陷在于该度量忽略了规则后件中项集的支持度。为了解决这一问题,引入Kulc度量指标来进行模式评估。

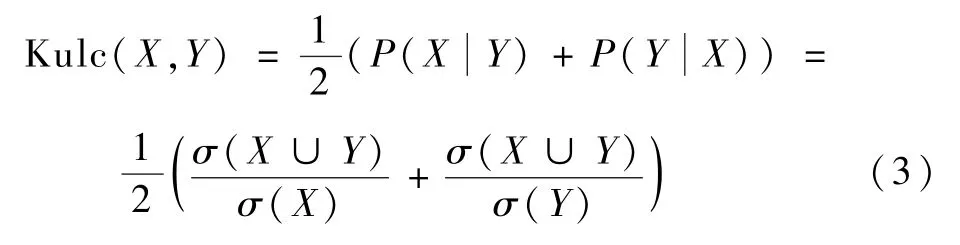
由式(3)可以看出,Kulc度量值仅受X、Y和X∪Y的支持度影响,而不受事务总个数的影响,当Kulc(X,Y)＞0.5,则事务X与Y之间呈正相关;当Kulc(X,Y)＜0.5,则事务X与Y之间呈负相关;当Kulc(X,Y)=0.5,则事务X与Y之间无明显关联,且Kulc(X,Y)的值越靠近0.5,则X与Y之间的关联程度越弱。

定义6不平衡比度量指标(IR)。不平衡比度量指标是评估规则蕴含式中项集X与Y之间的不平衡程度,是对Kulc度量指标的补充。虽然当Kulc(X,Y)的值接近0.5时,事务X与Y之间无明显关联,但是出现这样的关联规则有可能是因为事务中出现了0事务,即不包含任何考察项集的事务,所以得对Kulc(X,Y)接近0.5的值用IR指标进行二次考察,若IR(X,Y)值接近于0,那么事务X与Y之间的确毫无关联;若IR(X,Y)接近于1,则事务X与Y之间关联较强,即分析出的关联规则可用。不平衡比度量指标定义为

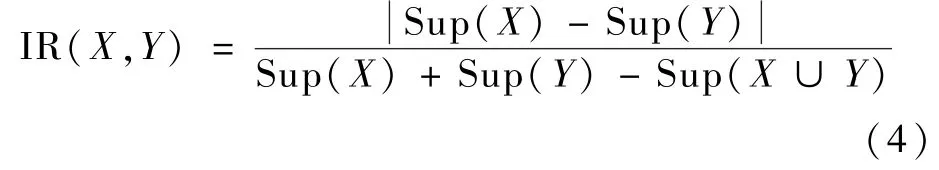
定义7FP树。将数据集中的各个事务数据项按照支持度排序后,把每个事务中的数据项按降序依次插入到一棵以NULL为根节点的树中,同时在每个节点处记录该节点出现的支持度,最终构造出FP树。FP-Growth算法采用分治策略将一个问题分解为较小的子问题,每一次递归,通过更新前缀路径中的支持度计数和删除非频繁项来构建条件FP树。举一具体实例展示FP树及条件FP树的生成过程。

算法第1次扫描数据集,计算出各参数频数,并设定最小支持度,将频数小于最小支持度的参数项进行删除,依据频数将每条数据的参数从大到小重新进行排列,过程如图4所示。

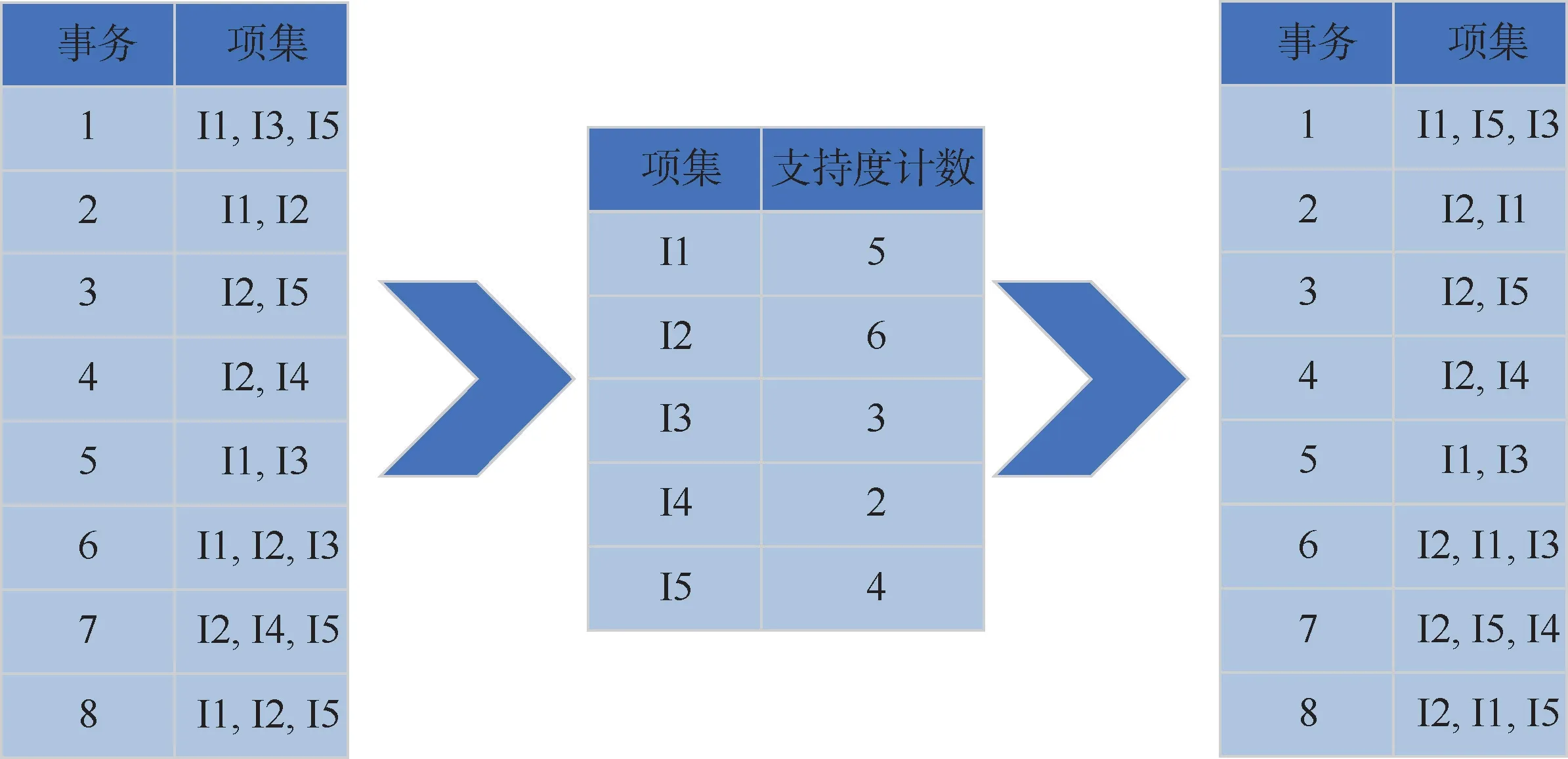
图4 参数频数统计及数据中参数重新排序Fig.4 Parameter frequency statistics and parameter reordering in each piece of data

紧接着算法第2次扫描数据库,从根节点“NULL”出发,依次将每条数据读入,出现相同的节点进行累加,如所给例子,先读入TID1生成第1条分支;之后读入第2条数据形成第2条分支;再读入第3条数据,由于与第2条数据有共同的参量I2,所以在I2节点上计数加1,以此类推将数据集遍历一遍生成FP树,过程如图5所示。

依据生成的FP树依次考察末节点,删除末节点所包含的前缀路径,该路径剩余节点构成的树即为该考察节点的条件FP树。各末节点对应的条件FP树如图6所示。

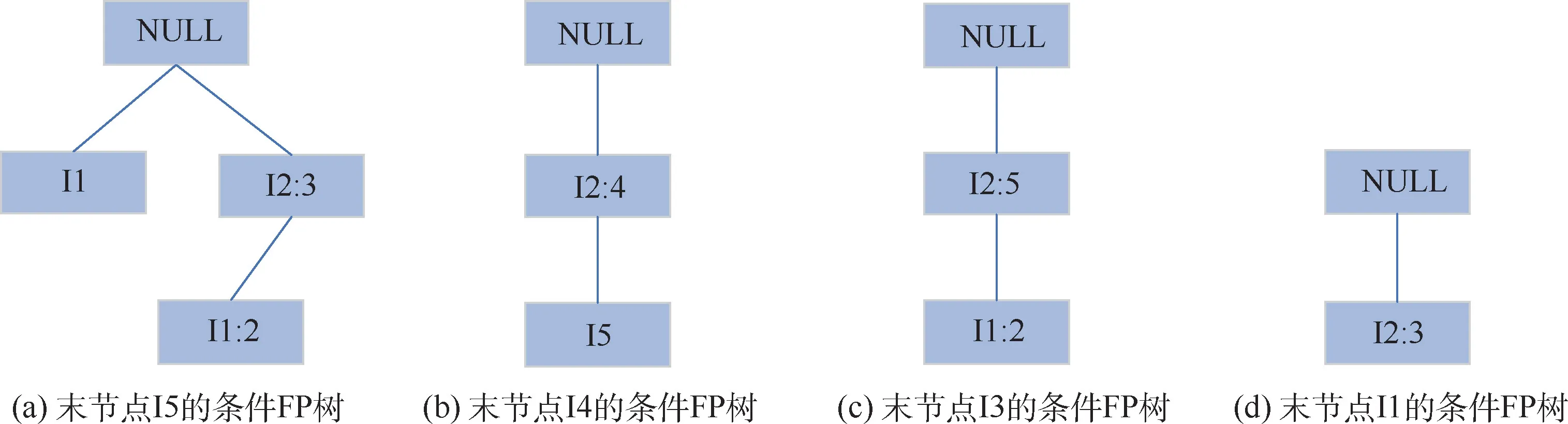
图6 各末节点对应的条件FP树Fig.6 Conditional FP tree for each final node

3.2 干扰量数据格式处理

FP-Growth算法需要将实在意义的干扰量参量转化为数据格式标签,即将不同数据类型的干扰量参量进行统一编号;将带有编号的数据导入FP算法进行挖掘分析;最后根据其编号参量具体的物理意义,得出相应的关联规则。将干扰量参量编号后的结果如表5所示。

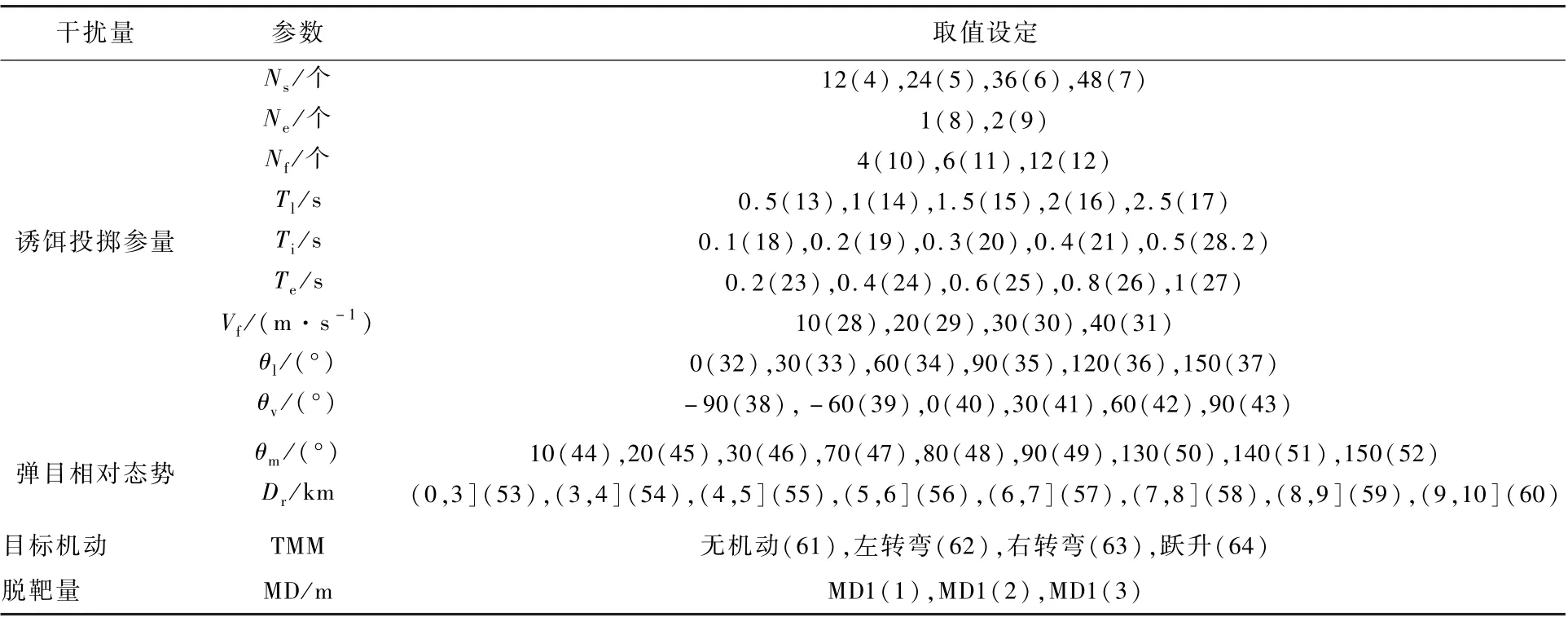
表5 干扰量参量编号Table5Disturbance variable numbering

4 试验分析

通过第2节构建的数据立方体统计出数据集中各事务的支持度计数,来减少FP-Growth算法遍历数据集的次数,从而提高该算法生成关联规则的收敛速度,收敛速度的比较将在4.3节中论述。本文所构建三维立方体,将最后挖掘算法得出的关联规则进行划分:①各方体内部的关联规则挖掘,旨在得出各干扰量之间应该如何组合使用才能对导弹的干扰效果影响最大,从而保证载机的安全;②方体间外联关联规则的挖掘,通过对各个方体之间的关联规则进行比较,得出对脱靶量影响较大的干扰量。

4.1 各方体内部关联规则

由于试验中感兴趣的低命中率结果总数相对于整个数据集合为少数,采取低支持度度量指标,防止将感兴趣的规则剔除掉,故将最小支持度指标(minSup)设置为0.5%,最小置信度指标(min-Conf)设置为0.7;Kulc度量指标的边界条件设定为Kulc＜0.4或Kulc＞0.6;若0.4≤Kulc≤0.6时,则判断不平衡比度量指标(IR),并且最小不平衡比度量指标设置为minIR＞0.9。

1)MD1＜12m内部关联规则

对MD1子立方体中的数据,按照所设置的各指标条件,进行关联规则的挖掘,对挖掘出的关联规则进行筛选。其部分的关联关系如表6所示。

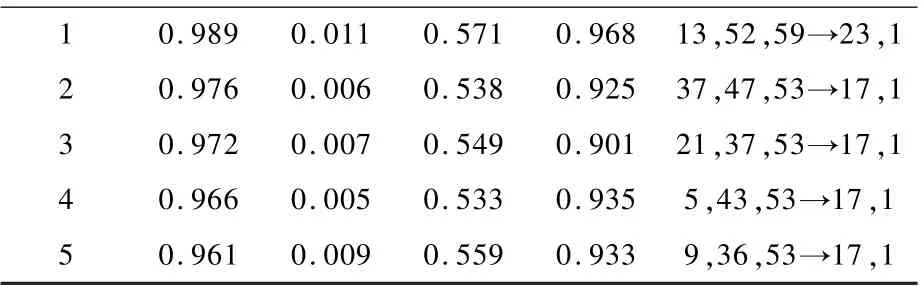
表6 MD1部分内部关联规则(MD1＜12m)Table6 Inner association rules of MD1(MD1＜12m)

序号 Conf Sup Kulc IR 规则

通过分析表6可得到以下结论:

①序号1规则。该规则的置信度达到了0.989,说明了导弹做迎头攻击,在弹目距离较远(8～9km)的情况下,若载机诱饵起投时间早,则载机不应该再采取小间隔投掷策略,否则很快就会将诱饵投掷完毕,在拦截末期目标将无诱饵可用,载机未将导弹完全诱骗,导弹又重新将载机识别,最终脱靶量较低。

②序号2～5规则。表6规则都有较高的置信度,说明当弹目距离非常近的时候(小于3km),红外诱饵弹的起投时机不应该过晚,否则有可能诱饵还未投掷结束,导弹就已经命中载机,干扰效果极差。

通过表6分析可知,根据弹目距离选择诱饵的投掷方式对干扰的效果起到决定性作用,弹目距离远应选择“晚起投+大间隔”的投掷方式;弹目距离近应选择“早起投+小间隔”的投掷方式。

2)12m≤MD2＜16m内部关联规则

针对该立方体中的数据,进行关联规则的挖掘,挑选部分感兴趣的关联规则进行分析,规则在表7呈现。

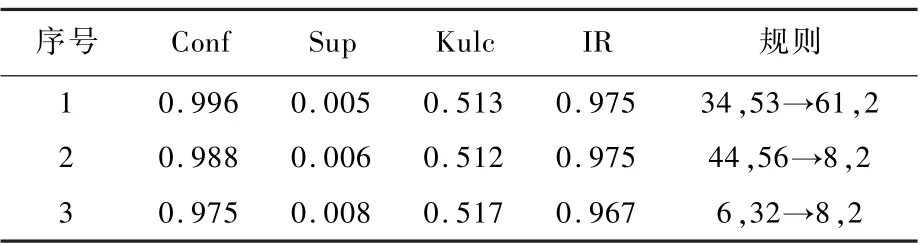
表7 MD2部分内部关联规则(12m≤MD2＜16m)Table7 Inner association rules of MD2(12m≤MD2＜16m)

通过表7规则可以得到如下结论:

①序号1规则。在迎头攻击的情况下,载机无需采取机动就可以获得较好的干扰效果。

②序号2、3规则。若载机的诱饵总数固定,导弹采取尾后攻击方式,当弹目距离较远时,载机可以采取每次单投1个的投掷策略,目的是为了延长红外诱饵的干扰时间,使其持续干扰。

通过表7分析可知,导弹要尽量避免采用迎头攻击方式,若导弹采取尾后攻击,载机要想办法调整干扰策略,使其干扰时间延长,从而增强干扰效果。

3)MD3≥16m内部关联规则

该组数据的挖掘结果如表8所示。

表8 MD3部分内部关联规则(MD3≥16m)Table8 Inner association rules of MD3(MD3≥16m)

对表8数据加以分析可得如下结论:

①序号1、2规则。当弹目距离较远(9～10km)时,若载机采取“晚起投+大间隔”的投掷策略,导弹脱靶的概率达到0.986。

②序号3、4规则。当弹目距离较近(小于3km)时,载机想要保证对导弹的干扰效果,应采取“早起投+小间隔”的投掷策略。

由表8分析可得,弹目距离在9～10km之间时,采取“晚起投+大组间”的投掷策略;在弹目距离小于3km时,采取“早起投+小间隔”的投掷策略,可以获得良好的干扰效果。

通过对各立方体内部关联规则的分析,可以得到以下结论:

1)导弹要尽量避免采用迎头攻击的攻击方式。

2)根据弹目距离的远近,选择合适的起投时机以及投掷间隔。

3)干扰参量的随意组合会造成干扰效果的下降。

4.2 方体间外联关联规则

按照4.1节设置同样的度量指标边界条件,对方体间外联关联规则进行筛选,得到如表9所示部分方体间外联关联规则。

选取表9中最具代表性的部分方体间外联关联规则进行分析。

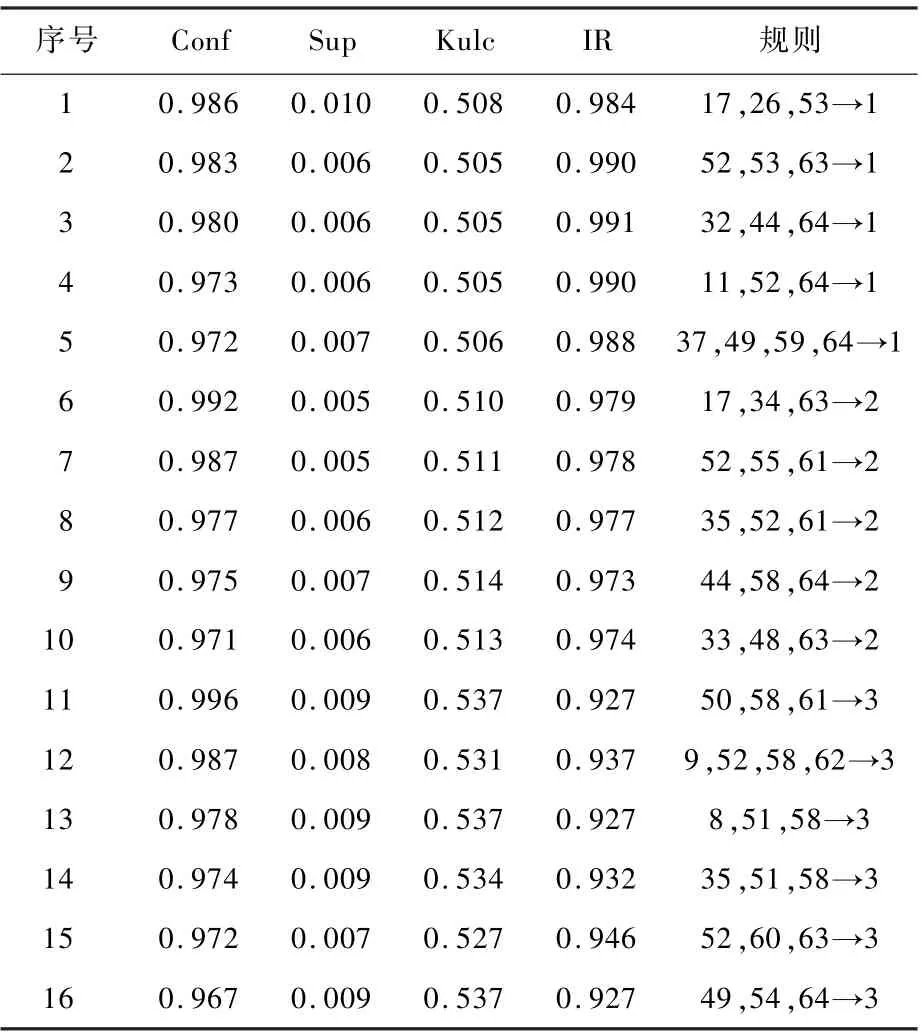
表9 部分方体间外联关联规则Table9 Part of outer association rules

1)序号1规则。17,26,53→1,过了2.5s后目标以每组组间间隔为0.8s开始投掷红外诱饵弹,弹目距离小于3km,在这种干扰态势下导弹脱靶量小于12m的置信度达到0.986。分析原因为弹目距离过近,若目标投掷诱饵的起投时机晚,并且采用大间距时间间隔投掷策略,导弹可能已经进入了盲飞区,此时诱饵已经不能对导弹造成干扰,故干扰效果极差,在这种情况应采取“快速、短频”的投饵方式。

2)序号6规则。17,34,63→2,过了2.5s后目标以60°水平投掷夹角投掷诱饵弹,同时采取右机动规避导弹,在这种干扰态势下导弹脱靶量介于12～16m,置信度为0.992。分析原因为目标诱饵弹起投时机晚,目标采取右机动规避导弹的同时投掷诱饵,并且投掷方向与机动方向一致,这样就使得诱饵尽可能的覆盖了目标,同时增加了覆盖时长,这样对导弹的干扰效果大大加强,最终造成脱靶量上升。

3)序号3与序号9规则。规则3与规则9相比,若导弹采用尾后攻击方式,同时目标采取跃升机动方式进行规避,此时采取的诱饵投掷方式应该是垂直方向投掷而不是水平方向,原因是要让诱饵尽可能的将发动机尾焰进行遮挡,使得诱饵在导引头视场中停留时间足够长,从而增加导引头的识别误差,降低命中精度。

4)序号11～15规则。通过这5条规则可以发现都有一个共同的干扰因素,即导弹以大进入角方式对目标进行追踪,进入角大于130°的范围属于前半球面,攻击方式属于迎头攻击,在这种情况下目标蒙皮对发动机尾焰遮挡严重,目标释放的红外诱饵弹为高辐射能量区域,极易诱骗导弹朝诱饵弹方向飞去,以致于目标花费极低的代价,仍可造成较大脱靶量,如规则11,目标无需采取任何机动方式,导弹依旧未跟踪到目标。

5)序号4规则。由序号11～15规则分析可知,当导弹做迎头攻击时,目标只需花费少许代价便可使干扰效果显著。但如果导弹做迎头攻击时,同时目标采取跃升机动方式进行规避,这使得被蒙皮遮蔽的发动机尾焰暴露在导引头视场中,从而使得干扰效果大大下降,故导弹为迎头攻击时,载机最好不要采取跃升机动对其进行规避。

6)序号2、7、11规则。虽然序号7规则进入角大于序号11规则的进入角,但是由于弹目距离的不同造成干扰效果不同。在序号11规则中,由于弹目距离远,虽然导引头有足够时间识别目标并做弹体姿态调整,但由于目标蒙皮对尾焰的遮蔽,使得目标与诱饵的红外辐射能量差异过于悬殊,导引头识别误差越来越大,最终跟丢目标;序号7规则,由于弹目距离较近,诱饵还未将导弹完全诱骗,此时导弹已经进入盲飞区,将不再受诱饵干扰,故干扰效果下降,脱靶量下降;而序号2规则,最后的结果更能说明这一结论,弹目距离太近(小于3km),即使导弹以大进入角进入,相对态势较差,但仍能保证较高命中率。

7)序号5与序号16规则。当导弹的进入角为90°时,目标采取跃升机动进行规避,此时导弹速度与目标速度垂直,两者相对速度达到最大,目标采取的机动方式虽然导引头能够识别,但是在这种情况下导弹没有足够的过载对弹体姿态进行快速调整,如序号16规则,又因初始弹目距离较近,就更没有足够的时间给弹体进行姿态的调整,同时加上红外诱饵弹的干扰,在“双重干扰”的条件下,造成了最后脱靶量较大。但序号5规则,红外诱饵弹的投掷方向与导弹来袭方向同向且异侧,干扰效果大大降低,与此同时弹目距离较远,导弹有足够的时间进行弹体姿态的调整,故脱靶量大大降低。

通过对上述关联规则的分析可以得到以下结论:导弹的进入角与弹目距离是影响干扰效果的主要因素;诱饵的投掷方向要与目标机动及导弹来袭方向配合使用,使得诱饵弹对发动机尾焰的遮蔽时间尽量长,将会提升干扰效果。

4.3 规则挖掘效率验证

为了说明在不同数据量下的传统FP-Growth算法与基于数据立方体处理数据后的FP-Growth算法(DC_FP)的挖掘效率,本试验分别在数据量为1000,5000,10000,15000,20000,50000进行2种算法的对比,置信度设置为0.7、支持度设置为0.5,对比结果如表10所示。

表10 不同数据量下算法效率对比Table10 Comparison of algorithm efficiency with different data volumes

该对比试验是在同一电脑硬件下完成的,由对比的结果可知,传统的FP-Growth算法与DC_FP算法在小数据规模下,算法效率相当,但随着数据规模的增大,传统的FP-Growth算法与DC_FP算法之间的计算效率差距也越来越大,尤其当数据量超过10000条后,传统的FP-Growth算法的挖掘效率下降明显,原因是由于数据维数较多(13维),造成每条数据划分为的子问题多,同时又要遍历数据集统计各项集的支持度计数,故造成了算法性能的下降。