基于障碍物代价势场的移动机器人避障算法
2022-11-30迟胜凯谢永芳陈晓方彭帆
迟胜凯,谢永芳,陈晓方,彭帆
(中南大学 自动化学院,长沙 410083)
随着机器人技术的快速发展,机器人在工业、服务业、安防等领域的应用越来越广泛,机器人也越来越多的出现在生活中。移动机器人最重要的功能是路径规划和避障,导航的目的是找到从起点到终点具有避障能力的最优或次优路径[1]。现实世界的环境是动态变化的,需要不断更新地图中的障碍物信息,使机器人在现实环境中实现灵活的自主移动。因此,在保证路径规划最优或次优的前提下,如何让机器人对场景中的静态和动态障碍物快速的做出响应,同时保证路径的平滑度和安全性,对于机器人的避障来说非常重要。
机器人所处的环境通常是三维的,三维环境地图[2-3]是描述真实三维世界最直接的方法,在三维地图中可以获得障碍物更多的形状、轮廓、姿态、语义等信息,对于辅助机器人的导航和避障来说意义重大。而基于三维点云地图的三维路径规划[4]具有很高的时间复杂度和空间复杂度,不利于实时避障的实现。因此在二维地图场景下利用三维障碍物信息,实现基于二维地图的导航和路径规划,对于提高机器人避障的灵活性是很有必要的。
栅格法环境建模是移动机器人导航的经典方法,该方法将机器人所处的实际环境分割为大小相同的栅格,每个栅格的不同值对应地图的不同障碍物占用状态[5]。因此在栅格地图下利用三维场景信息及三维传感器数据,可以大大提升移动机器人导航与避障的灵活性与安全性。在栅格地图场景下,常用的路径规划算法有A*算法、人工势场法、蚁群算法、快速扩展随机树(rapidly-exploring random tree star,RRT*)算法、遗传算法、D*算法等[6]。A*算法是求解最优路径非常有效的算法,但是当路径规划的场景较大时,并且存在障碍物遮挡时,A*算法的计算量就会非常大,内存占用严重,并且运算时间长,路径规划的效率较低,赵晓等[7]针对此问题提出了基于跳点搜索的改进算法,通过筛选跳点进行扩展,直到生成最终路径,扩展过程中使用跳点代替A*算法中大量可能被添加到有效点集合和无效点集合的不必要节点,从而减少计算量。王洪斌等[5]针对多目标复杂场景,提出了A*算法与动态窗口法相结合的混合算法,通过设置多个临时目标点,利用目标成本函数对所有目标进行优先级判定,进而利用改进的A*算法规划出一条经过多个目标点的最优路径,一定程度上改善了算法的效率问题,但是对于导航路径的安全性及路径平滑性的问题,依然没有很好的解决。Liu等[8]采用了改进蚁群算法进行全局路径规划,在搜索全局路径的过程中,将信息素扩散与势场力相结合,使信息素沿障碍物势场力的方向扩散,提高了蚁群算法的收敛速度,但蚁群算法为找到全局最优路径,搜索空间必须足够大,会消耗大量的内存空间,依然存在最优路径搜索效率低的问题。林依凡等[9]提出了一种无碰撞检测改进RRT*运动规划算法,针对RRT*算法碰撞检测过程中耗时过长的问题,提出使用在代价函数中增加碰撞风险评估函数的方法取代所有的碰撞检测计算,提高了算法的寻路效率,但是并没有改善导航的路径平滑性不好、算法不稳定的特点,且没有考虑与障碍物的安全距离。薛学华等[10]提出了一种改进人工势场法,针对局部最优值问题提出了一种自适应参数调整回溯法,解决了传统人工势场的路径不可达与局部最优值问题,通过人工势场法与可视图法切换的策略克服了人工势场目标不可达问题,但是该算法同样没有考虑导航路径的安全性及平滑性,且得到的路径长度通常不是最优的。
Zafar和Mohanta[6]对目前现有的移动机器人的路径规划和避障算法及改进方案进行了研究和对比,现有研究在解决同一场景下机器人避障问题时只考虑了单一的路径评价指标,如只考虑路径最短、平滑度最优、耗能最少或算法的效率最高,在单一指标上能够达到较优的效果,因此只能适用一些特定的场景。以往研究的另一个局限是,在进行静态或动态环境下局部路径规划过程中,没有考虑机器人的大小,也没有考虑移动中的障碍物对于移动机器人避障的影响。而在一些工业应用场景下,不仅要求路径尽可能地短,出于安全考虑需要机器人和某些障碍物保持安全距离,并且要求路径具有较高的平滑度。
基于以上原因,本文提出了一种基于障碍物代价势场的动态路径生成及路径调整算法。根据激光雷达、深度相机等传感器数据获取动态障碍物运动状态信息。然后由栅格地图构建障碍物的代价势场,根据机器人的形状、大小及其他避障参数选择某一合适高度的等势曲线,通过求解由机器人当前位置、目标点、等势线及其切线得到的最小生成子树,获得初始候选路径。对初始候选路径采样获得初始候选路径锚点。并在代价势场下对初始候选路径锚点的障碍物代价和路径长度代价进行调整,得到最终的路径。算法在保证路径和障碍物的安全距离以及较好的路径平滑度的同时,能够使规划得到的路径尽可能地短。对于动态移动的障碍物,通过引入障碍物速度对代价势场的影响,使得在移动障碍物场景下也能获得较好的结果。
1 机器人避障问题建模
1.1 机器人模型
在平面环境中,差动转向移动机器人的机械结构简单、运动灵活、稳定性高,是目前较为流行的地面移动机器人。本文假设机器人装有稳定的底层控制系统,可以通过陀螺仪、激光雷达、里程计等传感器数据完成对机器人速度、姿态的跟踪。设E-N为机器人所处的世界坐标系,X-Y为机器人本体的坐标系,如图1所示,机器人的当前状态可以用一个向量[e,n,θw]表示,其中[e,n]表示机器人在世界坐标系中的坐标,θw表示机器人的航向角。设机器人左右两侧驱动轮距离为W,驱动轮直径为L,右轮和左轮角速度分别为和,机器人的运动状态可以表示为
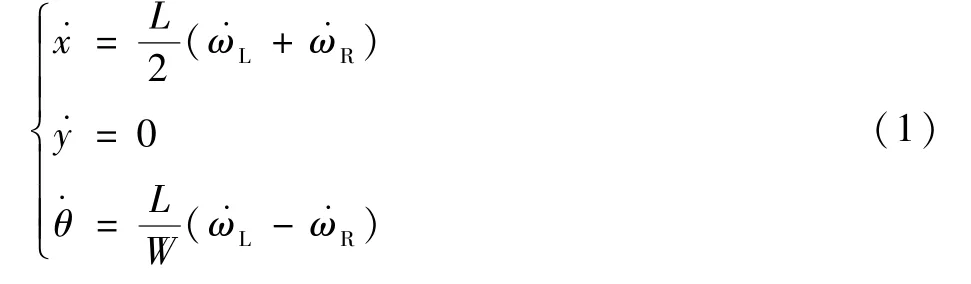

图1 差动转向机器人的俯视示意图Fig.1 Top view of differential steering robot

1.2 动态地图模型
虽然机器人只会在一个二维的平面内运动,但机器人所处环境是三维的,而直接在三维地图下进行路径规划和避障,会使计算的复杂度大大增加,不利于实时的实现和大尺度环境下的应用。为了在导航过程中充分利用三维数据,实现本文的避障算法,通常基于多线激光雷达数据实现动态地图的更新,通过建立由三维点云数据到二维占用栅格地图的动态映射来更新动态障碍物地图信息。由本地机器人在动态二维地图的基础上完成避障任务。
机器人在进行导航和避障之前会建立一个全局场景的静态栅格地图,假设这个初始场景的栅格地图不会发生变化。机器人在运动过程中会对激光雷达产生的点云数据进行实时处理,根据具体机器人的大小和尺寸进行滤波去除无效的点云信息,利用可能会与机器人发生碰撞的障碍物有效点云信息更新对应的障碍物占用栅格地图[11](occupancy grid map),得到针对不同动态障碍物的动态概率栅格地图,即不同栅格中存在障碍物的概率。根据占用栅格地图中的障碍物表示方法,对于地图中的任意栅格,定义栅格状态算子s,p(s=0)表示该栅格被障碍物占用的概率,使用p(s=1)表示该栅格不被障碍物占用的概率,二者的和为1,使用二者的比值Odd(s)=p(s=1)/p(s=0)描述当前栅格的障碍物占用状态,初始状态下默认p(s=1)=p(s=0)。
在地图更新过程中假设不同栅格间的状态变化互不影响,对于地图中的任一栅格单元,假设在t时刻之前的障碍物占用状态为Oddt-1(s),在t时刻有新的测量值zt,其在t时刻的障碍物占用状态按式(3)进行计算,Odd(s|zt)表示在zt发生的条件下s的发生概率。

由贝叶斯公式可知
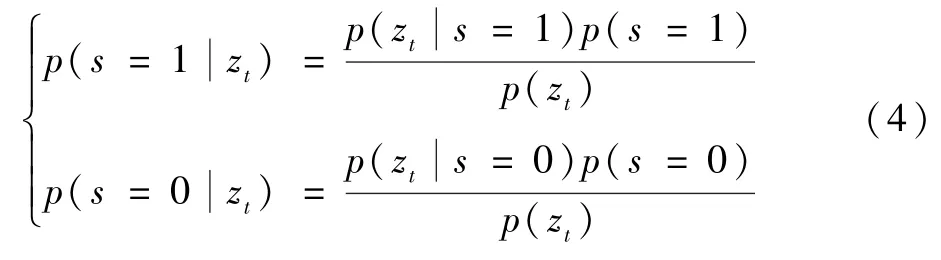
由式(4)代入式(3)后得
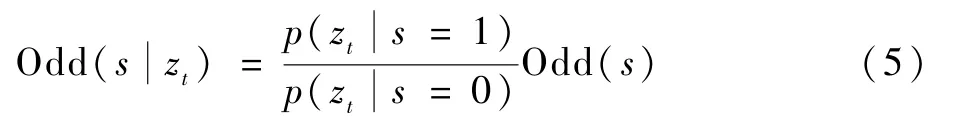
同时对式(5)两边取对数可得
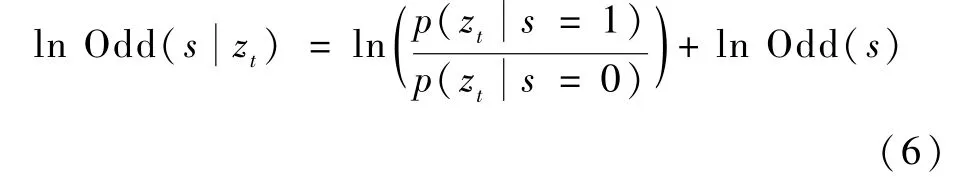
因此,只需根据当前传感器测量值对ln(p(zt|s=1)/p(zt|s=0))进行更新,即可实现障碍物地图数据的更新,记lt为t时刻栅格单元的对数占用状态式,lt-1为t-1时刻栅格单元的对数占用状态式,lmeas为传感器测量值的对数描述形式,则可以简化为lt=lt-1+lmeas。 测量值的模型有2种状态,分别为free和occupied,带迭代更新过程中都是定值。这样,即可基于占用栅格地图对动态障碍物进行描述,lt的值越大,则表示对应栅格存在障碍物的概率越大。在此基础设ρ为更新后得栅格障碍物概率描述式,Cmax表示地图中允许的栅格代价最大值,为一个常数。则当栅格的概率描述值lt<0时,ρ=0。当0≤lt<Cmax时,ρ=lt/Cmax,当lt>Cmax时,ρ=1。
假设本地机器人的全局静态栅格地图是由m1行m2列的栅格组成,则全局静态栅格地图可以用一个二维矩阵M(x,y)表示,栅格障碍物概率为

则由激光雷达数据得到的局部动态障碍物地图可以表示为M′(x,y)(其中x与y满足条件0<x<m1,0<y<m2)。在执行动态避障任务时局部动态障碍物地图会和全局静态地图进行叠加。
1.3 静态障碍物的表示
本文基于三维传感器数据得到了机器人对应的二维概率栅格地图,提出了基于障碍物代价势场的机器人障碍物表示算法。静态障碍物栅格的占用情况由栅格代价值C和栅格存在障碍物概率ρ这2个参数描述。先需要建立全局静态栅格地图的代价势场。设ρop=ρ为静态障碍物代价势场中的栅格障碍物概率,其中ρ为由占用栅格地图更新得到的障碍物概率,下标p为距离当前栅格最近且障碍物概率不为0的栅格、o为当前栅格。对于障碍物概率ρ≠0的栅格,其障碍物代价Up=Cmaxρop。对于障碍物概率ρ=0的栅格,障碍物代价为
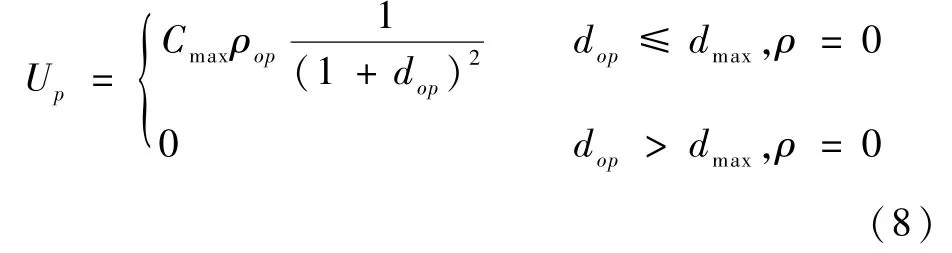
式中:若p(xp,yp)为距离当前栅格最近且障碍物概率不为0的栅格坐标,ρop为栅格p的障碍物概率;dop为p到当前栅格的欧氏距离;dmax为障碍物栅格所能影响的最远距离,为一个常数。这样可以得到静态栅格地图的代价势场,如图2所示,栅格的边长为单位1,黑色栅格代表障碍物概率ρ≠0的栅格,带有灰度的栅格为由式(12)计算得到的代价势场。

图2 障碍物附近的代价势场栅格示意图Fig.2 Schematic diagram of cost potential field grid near obstacle
1.4 动态障碍物的表示
在实际生产过程中机器人面对的不仅有静态的障碍物,还需要对场景中的动态障碍物做出灵活的响应。由三维场景下的激光数据可以获得动态障碍物相对于机器人的速度。根据机器人在世界坐标系下的姿态[e,n,θw],可以得到当前时刻动态障碍物坐标系相对于世界坐标系下的速度。定义Oobs[x,y]和v分别为动态障碍物当前时刻的位置和速度,其中[x,y]为动态障碍物对象位置,向量v为动态障碍物的移动速度,动态障碍物的移动速度为
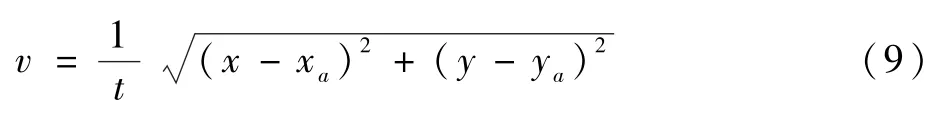
式中:A(xa,ya)为上一时刻动态障碍物的坐标;t为2次坐标更新的时间差。设B(xb,yb)为地图中障碍物概率ρ=0的任一栅格坐标,p(xp,yp)为动态障碍物Oobs中距离点B最近且ρ≠0的栅格坐标。令向量d=(xb-xp,yb-yp),障碍物速度对代价势场的影响为
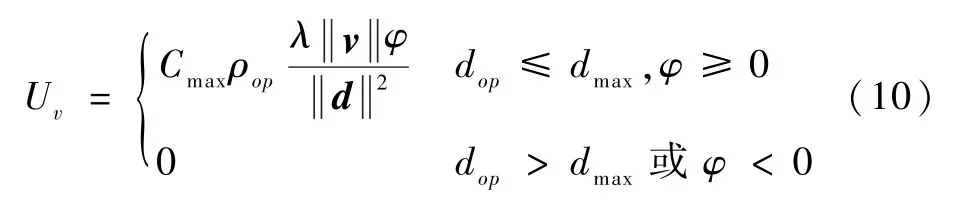
式中:λ为障碍物速度对代价势场的影响系数,值越大表示障碍物速度对障碍物代价势场的影响越大;ρop为栅格p的障碍物概率;φ为向量v和向量d夹角的余弦值,即

由式(8)和式(10)可得,动态障碍物场景下的障碍物代价为

2 路径生成与避障
2.1 切线的计算
为了计算避障过程中的初始候选路径,根据第1节本文算法计算栅格地图中的障碍物代价势场。如图3所示,在栅格地图中,设点R为机器人的当前位置,黑色栅格表示障碍物概率不为0的区域,白色栅格表示障碍物概率为0的区域,由式(12)更新障碍物代价势场,然后根据具体机器人的形状、大小、避障规则等选择合适高度的等势曲线。图3中红色曲线为障碍物的一条等势曲线,由于在栅格地图中长度的计算是不连续的,栅格地图中的等势曲线可以用图3中的绿色栅格表示。为方便计算,设点A为等势曲线的起点,按顺时针方向,等势曲线可以由一系列离散的栅格a1,a2,…,ane表示,其中ne为等势曲线包含栅格总个数。其长度lne按如下方法计算:

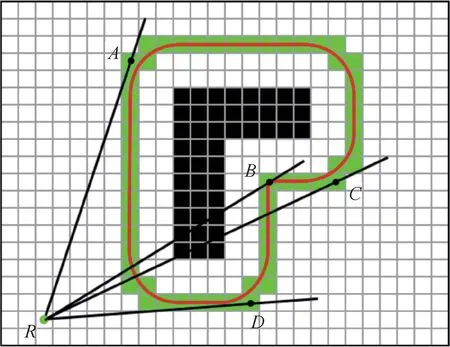
图3 基于代价势场计算切线及等势曲线长度Fig.3 Calculate tangent and equipotential curve length based on cost potential field
式中:di(i=1,2,…,ne-1)为栅格点ai到ai+1的曼哈顿距离,dne为栅格点ane到a1的曼哈顿距离。
为计算等势曲线的切线,需要计算等势曲线中栅格点与机器人当前时刻位置P0(x0,y0)间的斜率。设按顺时针方向栅格点ai(i=1,2,…,ne)坐标表示为(xi,yi),则经过栅格点ai的斜率si为
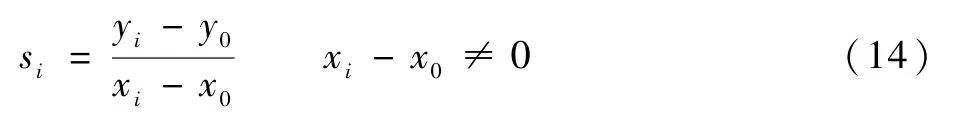
沿顺时针方向依次计算栅格斜率,在顺时针方向上斜率出现极值的栅格点即为等势曲线上的切点,如图3中的点A、B、C、D。对于出现斜率的绝对值无穷大的栅格点,需要进行单独判断,即判断等势曲线中其所在邻域内的栅格点是否出现在过该点与机器人当前位置R间连线的同一侧,如果是,则可判断为切点。
为了保证切点的有效性,需要保证在按顺时针方向寻找切点的过程中,相邻切点间的等势曲线长度大于常数dm,且相邻的有效切点不能出现相同的斜率,dm表示等势曲线上相邻切点间允许的最短等势曲线长度,一般设置为一个较小的数,其值越大则等势曲线上所允许的切点越稀疏。如图3中如果切点B与切点C间的长度小于dm,则可以认为切点B或切点C是无效的。对于求出的任意有效切点,如图3中的切点A,其到点R的连线长度表示为切点A到机器人当前位置R间的欧氏距离。
2.2 候选路径生成
根据得到的障碍物代价势场和切线的计算方法,可以得到不同障碍物的等势曲线及相应的切线。为了更好地描述在避障过程中候选路径的生成方式,如图4所示,图中没有画出具体的网格,其中黑色实线为障碍物的边界,包含实时检测到的动态障碍物,灰色曲线为其中一条障碍物代价值为hc的等势曲线。假设机器人当前位于点R,机器人当前的目标点为点G,为了得到最初的备选路径,分别计算经过点R和点G的障碍物等势曲线的切线,如图4的红色直线和绿色直线所示,为分别经过点R和点G的若干个切点。由于图中存在3个不连通的障碍物,等势曲线分为独立的3段,根据图4中切点所在的等势曲线可以将所有的切点分为3组,分别为set1={1,6,10,12}、set2={2,3,8,11}、set3={4,5,7,9},其中点R和点G自成一个分组。
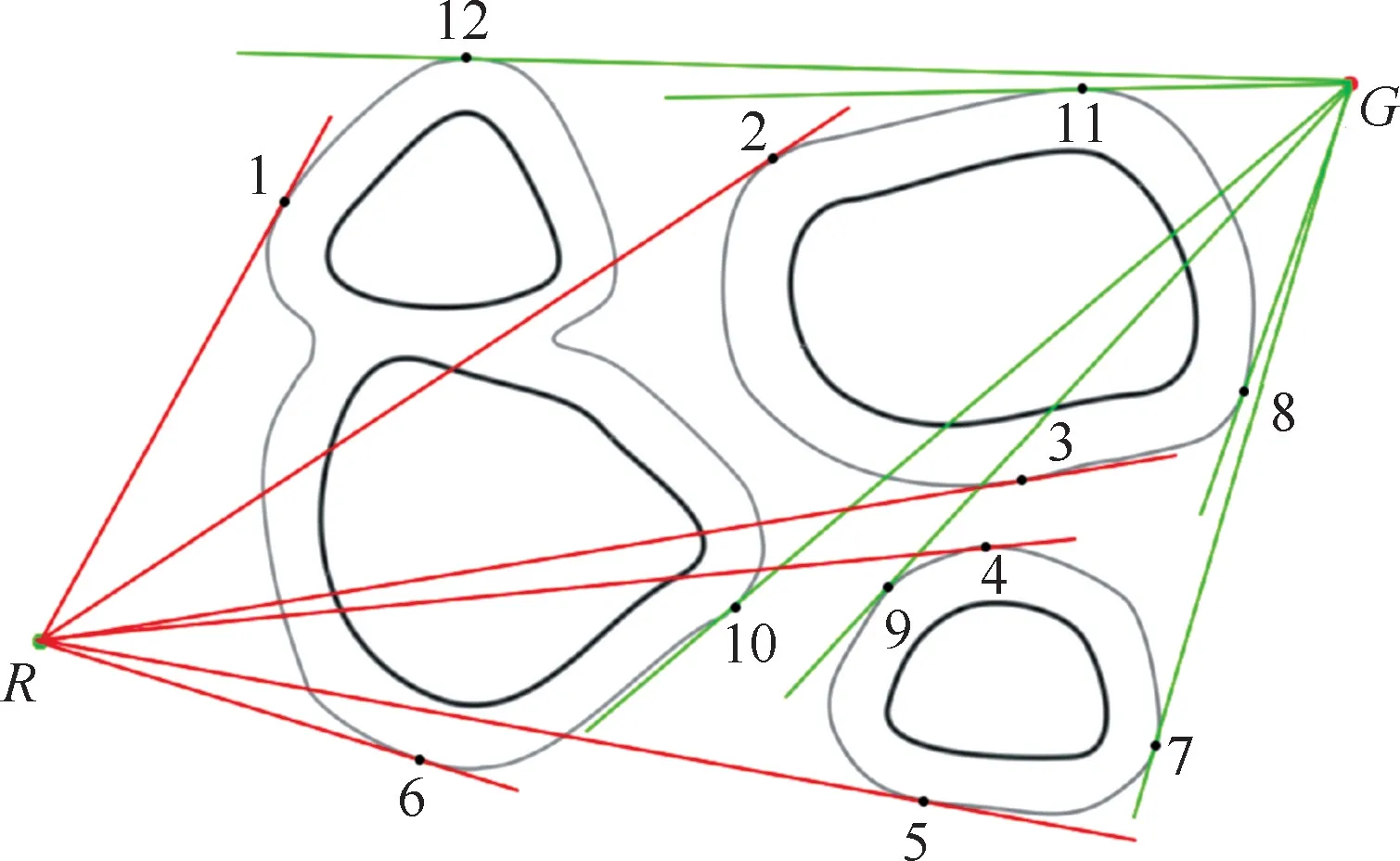
图4 障碍物等势曲线的切点Fig.4 Tangent point of obstacle equipotential curve
在实际求解过程中,每个分组内的切点数目是不确定的,假设包含起始点和目标点在内共有nt个节点,每个节点可以和剩下的nt-1个节点产生连接,而每2个节点间的连接是无向的,无需计算2次,因此可以得到连接的边数为nt(nt-1)/2,实际上在同一个分组内的点是不需要进行连接的;所以最终得到的有效连接数会少于nt(nt-1)/2。如图5所示,图中绘出的点10和点12的部分有效连接。
对2点之间的代价做如下定义:对于同一个分组内的任意2点,连接代价为其所在等势曲线上2点之间较短的一条曲线长度,即栅格代价较小的一侧。对于不在同一个分组内的两点,如果其间存在直线连接,并且没有穿越等势曲线,即没有穿过障碍物代价值为大于hc的栅格,其连接代价为2点之间的欧式距离,如图5中点R到点1之间的连接;如果其间的直线连接穿越了等势曲线,其连接代价为相应的等势曲线部分与2点间直线部分的长度之和,如图5中点12到点9之间的连接,其连接代价包含了两部分,一部分为点12和图中点p之间曲线连接中较短的一段等势曲线的长度,另一部分为点p到点9之间直线连接的长度。
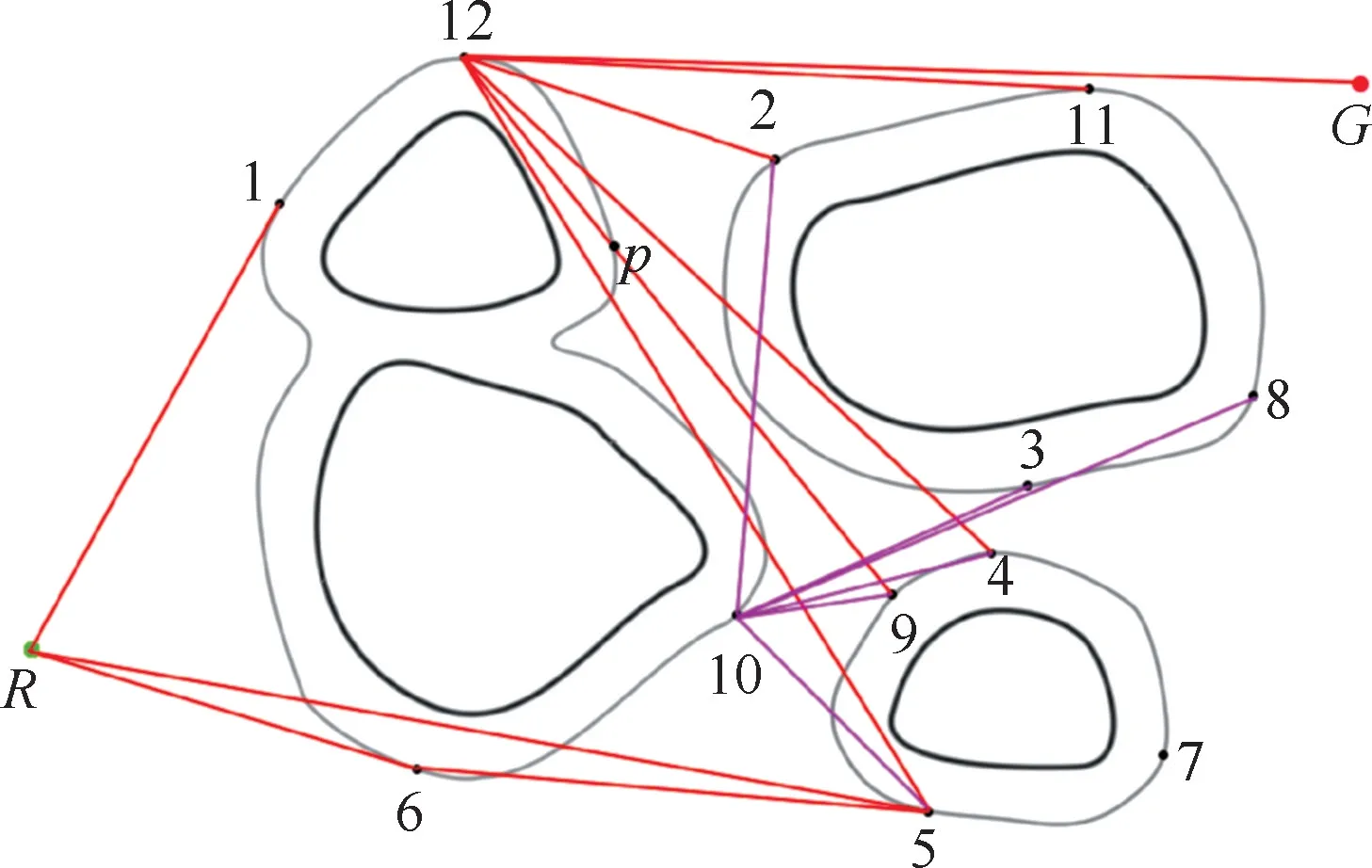
图5 基于等势曲线切点生成的部分连接代价Fig.5 Partial connection cost generated based on equipotential curve tangent points
应用切线计算方法和代价定义,可以得到包括机器人当前位置和目标点在内的所有切点之间的有效连接及相应的连接代价,所有的节点及其间的连接代价构成了一个包含起始点和目标点的无向图。为了找到一条可以从起始点到目标点的有效且连接代价最小的候选路径,需要对无向图进行遍历,可以采用深度优先或广度优先算法,或基于最小生成树的求解算法,求解包含起始点和目标点的最小子树,即为代价最小的有效路径。如图6所示,图中展示了3条连接代价较小的路径。
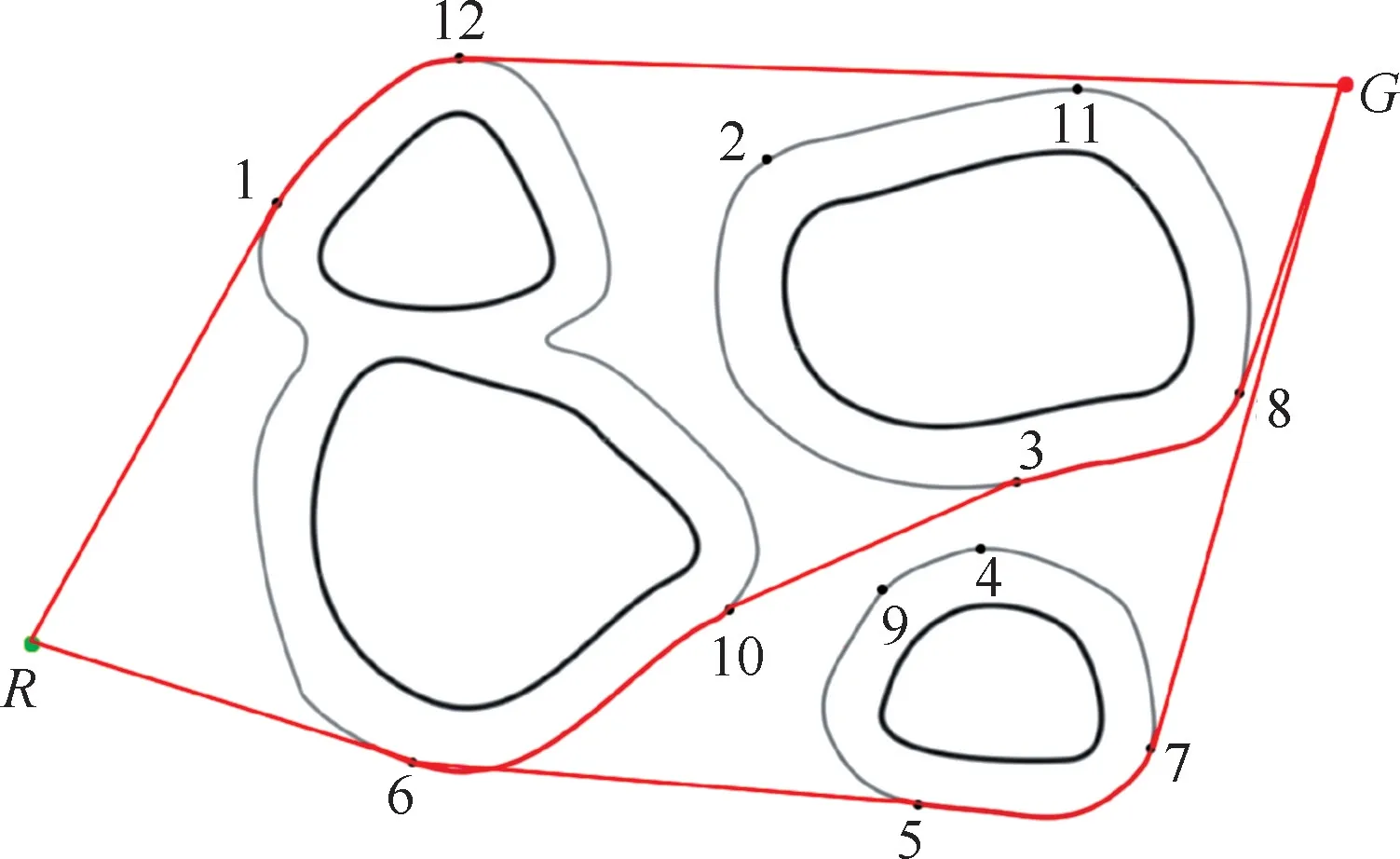
图6 由最小生成树得到的3条代价较小的初始路径Fig.6 3initial paths with lower cost obtained from the minimum spanning tree
通过路径生成规则,最终可以得到1条无碰撞的有效候选路径,记为P*,如图7所示,其中红色曲线为在U型障碍物中的初始候选路径,R为机器人的位置,G为当前目标点。此时得到的路径已经相对较为平滑,但对于机器人来说并不是一条代价最优的路径,需要对路径进行进一步的调整。
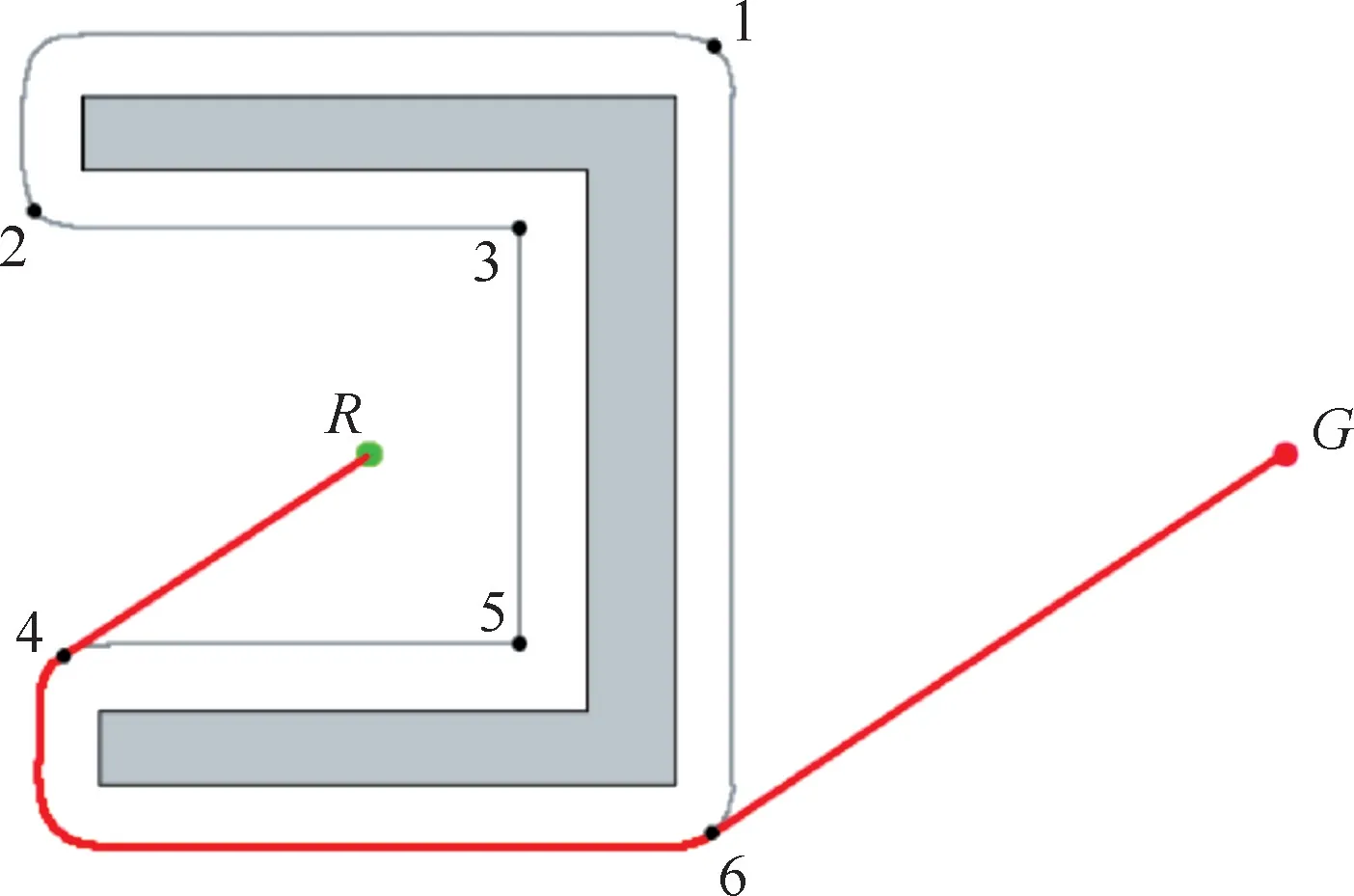
图7 U型障碍物中候选路径生成示意图Fig.7 Schematic diagram of candidate path generation in U-shaped obstacle
2.3 机器人不同初始姿态下的候选路径

图8 初试姿态及最小转向半径约束下的初始路径Fig.8 Initial path under constraints of initial attitude and the minimum turning radius
2.4 候选路径调整
在栅格地图中,初始候选路径是由紧密相邻的栅格表示的,不利于后续路径的调整,因此,需要对初始候选栅格路径按照一定的规则进行采样,得到一系列离散的点,称之为锚点。机器人的路径可以用一系列的锚点ps,p1,p2,…,pe表示,其中,ps表示路径起始点,pe表示路径终点。在采样过程中使用曼哈顿距离来表示栅格地图中2个栅格之间的距离。在调整过程中,相邻锚点间的距离过小会使锚点所受合力因相互抵消而变小,需要更多的调整轮数,同时也会增大计算量,距离过大则会使锚点过于稀疏,路径的平滑度变差,因此,为保证整条路径中锚点稀疏程度的一致性,设Dmax为路径调整过程中的采样间距,约定在对候选路径进行采样时,满足采样后相邻2个锚点之间的距离Di在小于常量Dmax的前提下取最大值。此时采样后的候选路径P*,可以由锚点集合P*={ps,p1,p2,…,pe}表示,如图9所示。
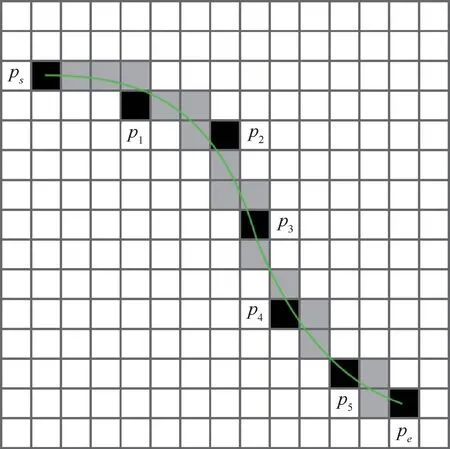
图9 栅格地图中初始路径采样表示Fig.9 Sampling representation of initial path in raster map
下面定义一种路径调整算法,将候选路径P调整为近似最短的安全路径。设锚点ps,p1,p2,…,pe所在栅格的障碍物代价值为cs,c1,c2,…,ce。则候选路径的障碍物代价Cobs为
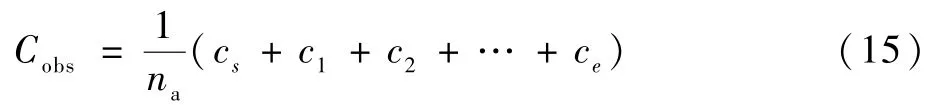
式中:ci为锚点所在栅格的代价值,cs为机器人当前位置的栅格代价值;ce为目标点的代价值;na为采样锚点的个数。
设锚点ps,p1,p2,…,pe中相邻锚点间的距离代价值为h1,h2,…,he。则候选路径的长度代价Hobs为
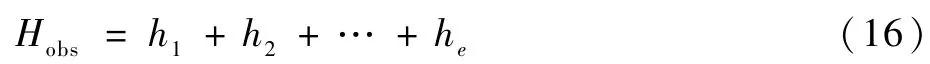
式中:hi(i=1,2,3,…,e)为相邻锚点之间的曼哈顿距离。此时机器人由当前位置到目标点加权代价Ccost为
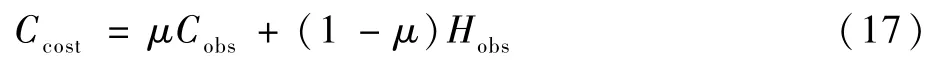
式中:μ为障碍物代价和距离代价对应的权值系数。
为了进一步对路径进行调整,定义相邻锚点之间存在吸引力。通过锚点之间的引力可以进一步调整候选路径的长度。约定每个锚点只会受到相邻锚点的影响而不会受到其他锚点的影响。设p1的坐标为(i1,j1),p2的坐标为(i2,j2),p3的坐标为(i3,j3),f1表示由点p2到p1的引力向量,f2表示由点p2到p3的引力向量,如图10所示,可以计算锚点p2受到的合力F2=f1+f2。此时锚点p2由于受到合力F2的作用沿F2的方向移动。若合力F2表示为(Fx,Fy),则锚点p2调整之后的坐标为p2(i2+σFx,j2+σFy),其中σ为调整增益,满足0<σ<1。
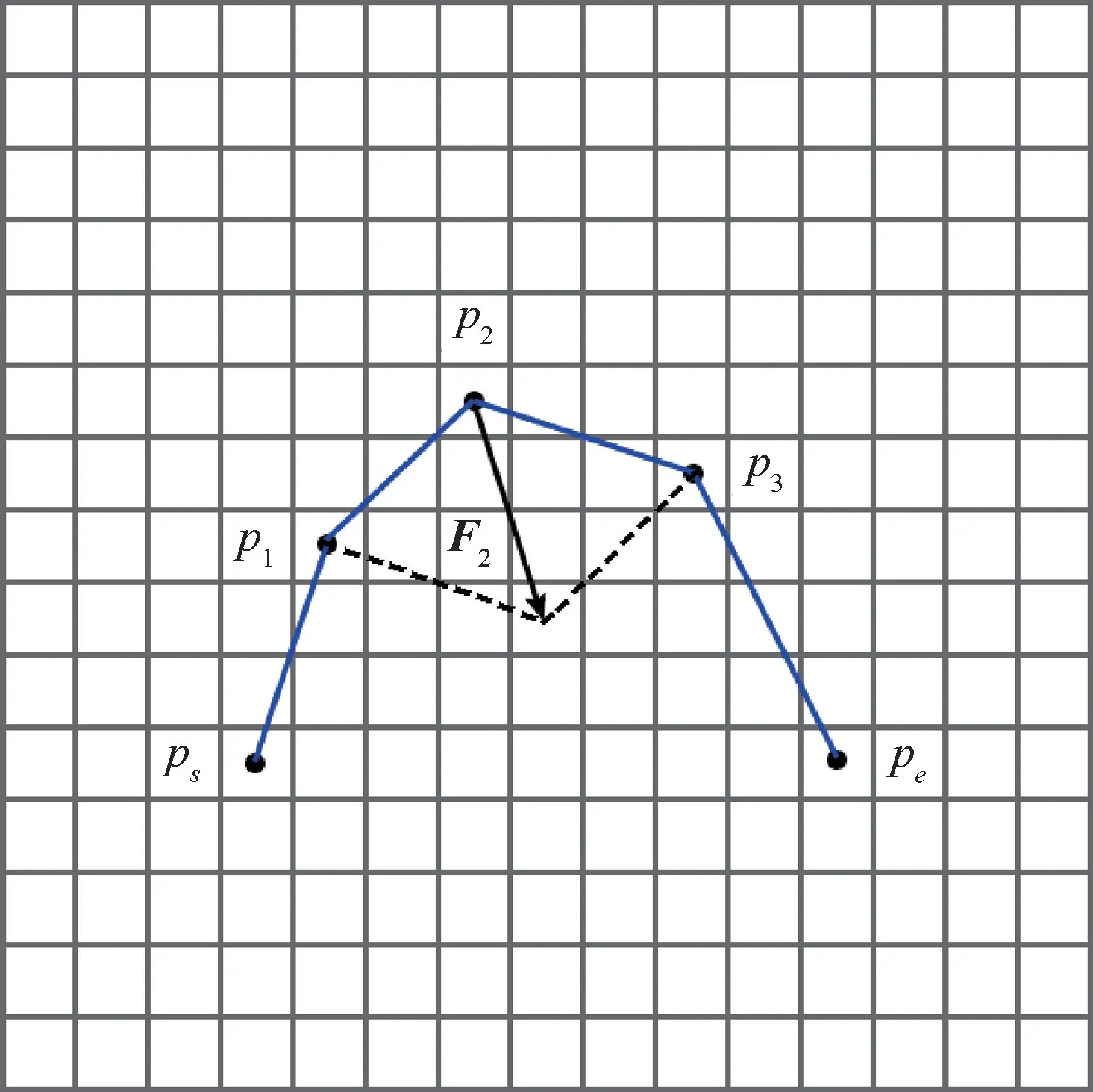
图10 候选路径中锚点p2所受合力F2Fig.10 Resultant force F2on anchor point p2in candidate path
为保证调整过程中整条路径中锚点稀疏程度的一致性,约定在路径调整过程中相邻2个锚点的距离Di满足约束条件:dmin<Di<2dmin,其中dmin为相邻2个锚点的最小距离,一般取dmin=0.75Dmax,并且初始锚点ps和目标点锚点pe为固定点,在调整过程中不会发生变化。当出现2个不相邻锚点pi-1和pi+1之间的距离Di<dmin时,可以通过删除锚点pi来满足约束条件。当2个相邻锚点pi-1和pi之间的距离Di>2dmin时,可以通过插入锚点pnew来满足约束条件,pnew的坐标为
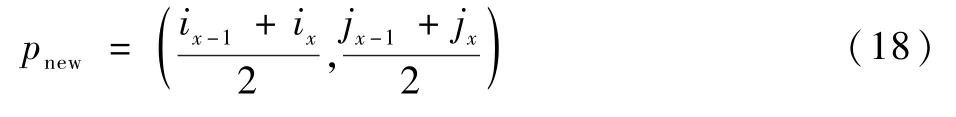
本节给出了在满足距离代价最优的条件下候选路径的调整方案,下面考虑在满足障碍物代价最优的条件下候选路径的调整方案。
在建立障碍物的二维栅格地图时,建立了从障碍物边界向外梯度下降的代价势场,用以表示机器人经过此处的障碍物代价。候选路径P*是由障碍物等势曲线得到的,因此可以基于障碍物代价势场对路径P*进行调整,使路径的总代价Ccost最小。
对于栅格地图中候选路径的每一个锚点,按照当前位置梯度下降的方向进行调整。需要计算每一个锚点处的梯度大小和方向,对于候选路径中的任意锚点p(i,j),以p点为中心的3×3栅格进行卷积计算。由梯度的计算式:
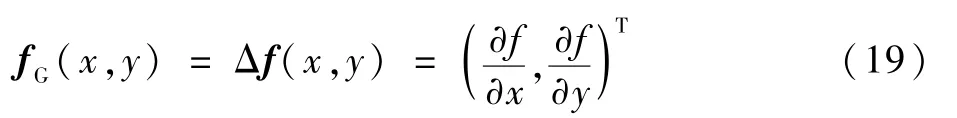
定义E(x,y)为代价势场中以锚点p为中心的3×3矩阵,则锚点p在x方向上的梯度为

可以得到锚点p的梯度大小为

由式(23)计算锚点p的梯度方向:

为了避免候选路径在调整的过程中因梯度方向的改变导致调整后的路径不平滑,定义单位向量g=(Gx/G,Gy/G)为梯度的方向向量。锚点p在x方向上的梯度调整量为

在y方向上的梯度调整量为
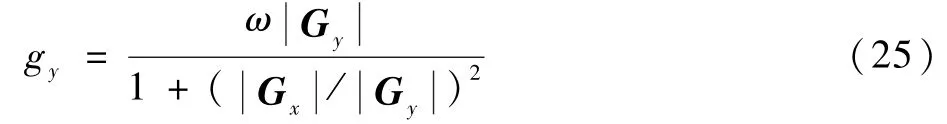
式中:ω为梯度调整量的增益系数。则锚点p在梯度调整后的坐标为p(i-gx,j-gy)。梯度下降的方向为当前待调整锚点在障碍物代价势场作用下的调整方向。候选路径的总代价Ccost为
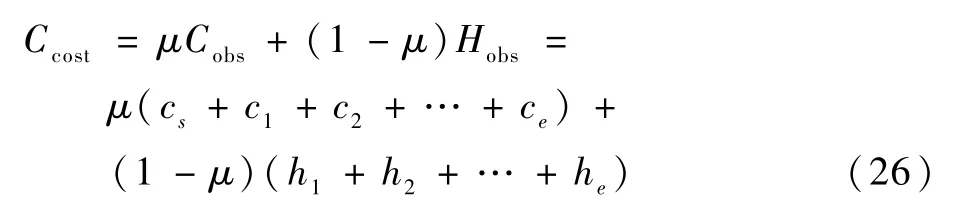
为了保证路径调整的可靠性,路径在每一步调整的过程中需要满足如下约束条件:
1)若hc为初始候选路径中所选等势曲线对应的障碍物代价值,在路径调整过程中候选路径中的任何一个锚点都不会从当前所在栅格移动到障碍物代价值高于hc的栅格。如果针对当前锚点的调整会使得调整之后的锚点所在栅格的障碍物代价大于hc,则跳过对当前锚点的位置调整继续调整下一个锚点。
2)如果考虑机器人的初始姿态及最小转弯半径R0,则应当保证调整之后的路径锚点不会出现在最小转向圆内部。如果针对当前锚点的调整会使得调整之后的锚点与最近的转向圆的圆心距离小于R0,则跳过对当前锚点的位置调整继续调整下一个锚点。
3)为了保证路径在调整过程中的平滑度,设Rmin(Rmin>R0)为路径调整过程中的最小曲率半径,对于任意相邻的3个锚点,其确定的圆半径r不小于最小曲率半径Rmin。在路径调整过程中,对锚点沿梯度方向调整和沿相邻锚点合力方向上的调整均会影响该锚点处的曲率圆半径,而在调整过程中不存在2种调整方式都使锚点处的曲率圆半径变小的情况,在对锚点沿梯度方向调整过程或沿相邻锚点合力方向上的调整过程中,针对已满足最小转弯半径条件的锚点,如果调整后的结果会破坏最小转弯半径的条件,则跳过对当前锚点的位置调整继续调整下一个锚点。如果初始路径中存在不满足最小转弯半径条件的锚点,针对这样的锚点,如果经过路径长度或势场代价的调整会使调整后的结果对应的曲率圆半径减小,则跳过对当前锚点的相应调整继续调整下一个锚点。因此,通过本文算法可以保证路径的平滑度,使路径满足最小转弯半径的约束条件。路径中锚点的转弯半径按式(27)进行计算。
图11为锚点p1、p2、p3所确定的曲率圆,p1的坐标为(i1,j1),p2的坐标为(i2,j2),p3的坐标为(i3,j3),圆心坐标O(x,y)为p1、p2与p2、p3所决定的2条中垂线交点决定,即解下面二元一次方程组:
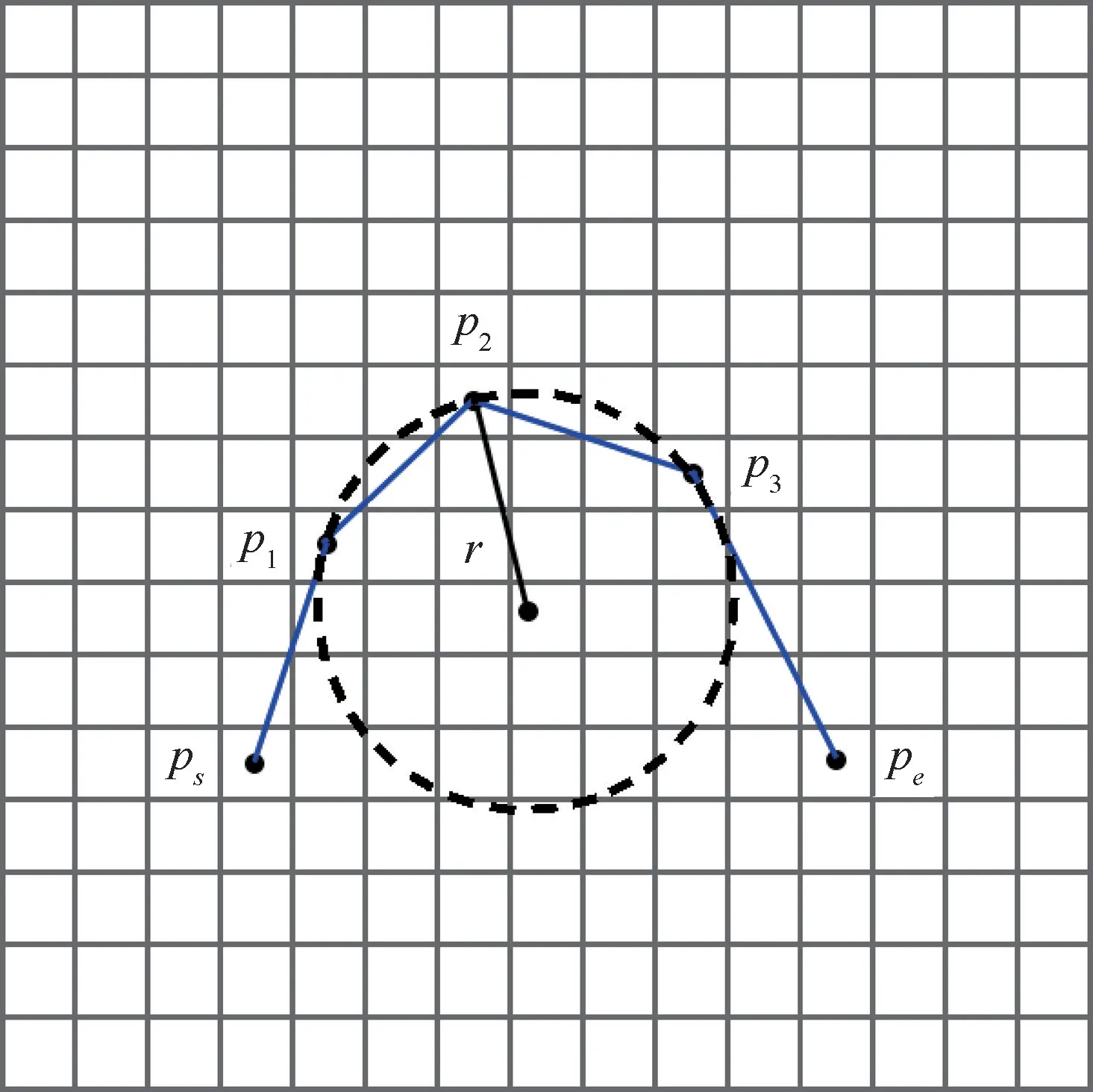
图11 锚点p2对应的曲率圆半径Fig.11 Radius of circle of curvature corresponding to anchor point p2

则p1、p2、p3所确定的曲率圆半径为
本文提出如下路径规划算法来调整候选路径P*,具体过程如下:
步骤1以Dmax为采样间距对初始候选路径进行采样,使得采样后相邻2个锚点之间的曼哈顿距离Di在小于常量Dmax的前提下取最大值,得到候选路径锚点集合P={ps,p1,p2,…,pe}。在调整过程中任意相邻的2个锚点的曼哈顿距离Di满足约束条件dmin<Di<2dmin,其中dmin为任意2个锚点的最小距离。
步骤2执行以下循环:
1)计算锚点pk(k=1,2,3,…,e-1)所受到的合力F(pk)。
2)尝试沿F(pk)方向移动锚点pk,判断从起始点到当前锚点的Cobs是否减小,如果是,则更新当前锚点。
3)判断锚点是否满足距离约束条件,如果Dk<dmin则删除锚点,如果Di<2dmin则插入新锚点。
4)循环执行第2步直至完成集合中所有锚点的调整。
步骤3执行以下步骤:
1)计算锚点pk(k=1,2,3,…,e-1)处的梯度大小和方向,并沿着负梯度的方向根据梯度的绝对值大小移动锚点pk。
2)判断锚点是否满足距离约束条件,如果Dk<dmin,则删除锚点,如果Di<2dmin则插入新锚点。
3)重复第1步和第2步,直至完成集合中所有锚点的调整。
4)比较第3步调整之后的路径总代价Ccost是否比调整之前小,如果是则第3步调整生效,否则不生效。
步骤4重复执行步骤2和步骤3并迭代更新锚点,直至Ccost的变化量ΔCcost<Ccon或循环达到一定次数,则退出循环。其中Ccon>0为一个给定的阈值。
根据本文提出的局部避障算法,可以得到一条由采样锚点构成,相对较短且安全的路径。机器人在实际路径跟随的过程中可以采用分段2次或3次样条插值法对调整后包含有限锚点的路径进行跟随。
3 实验与仿真
为了验证本文算法的特性,在MATLAB中进行了仿真。设定栅格地图的分辨率为1200×1000m。在本节中,分别验证了本文避障算法在静态障碍物环境中及包含移动障碍物的动态场景下的性能。在场景中,静态障碍物可以是墙、机器和设备。动态障碍物可以是行走的人,移动的设备或其他机器人。如图12所示,机器人可以通过静态栅格地图及基于传感器的障碍物信息生成包含障碍物速度信息的代价势场,并基于本文算法实现动态避障到达目的地。本文重点针对动态障碍物场景下单个机器人的避障进行仿真测试实验。
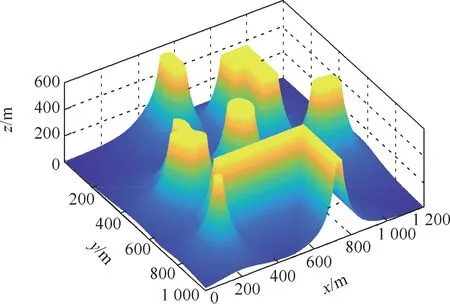
图12 静态栅格地图的代价势场Fig.12 Cost potential field of static grid map
3.1 静态场景下的避障分析
在计算机仿真中,通过计算栅格地图中障碍物栅格的代价,可以得到如图12所示的代价势场,高度越高的区域表示机器人由此处经过的代价越大。在更新障碍物代价势场时可以得到代价势场的等势曲线,图13为5组对应不同障碍物代价值的等势曲线。由图12与图13可知,等势曲线对应的代价值hc取值越大,则等势曲线越靠近障碍物。因此,为保证移动机器人导航过程的安全性,避免与障碍物发生碰撞,机器人导航过程中障碍物代价值hc的选择应使得等势曲线与障碍物的边界间的最短距离dc略大于0.5倍机器人的宽度或机器人外接圆半径,由图13可知hc的取值过小会使得路径过于远离障碍物进而无法通过一些狭窄的通道,因此实际应用中应根据机器人的具体外形参数选择合适的hc。其中令式(8)中dop的值取机器人的外接圆半径,此时计算出的Up的值即为hc对应的障碍物代价临界值。
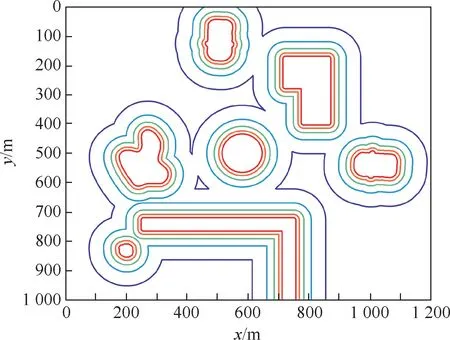
图13 障碍物代价势场的等势曲线Fig.13 Contour plot in cost potential field of obstacles
假设机器人当前位于点(550,900)m,向目标点栅格(950,100)m行进,如图14所示,其中黑色区域代表障碍物。取障碍物代价势场的最大值Cmax=600,初始候选路径中所选等势曲线对应的障碍物代价值hc=200,可以在图12所示的代价势场中得到对应代价值hc=200的若干段平滑的等势线。
然后分别寻找经过起始点和目标点的等高线的nt个切点,不同分组内的点,其间的连接代价包含栅格地图中的障碍物代价Cobs和距离代价Hobs。使用经典的Prim算法可以得到包含nt-1条边的最小生成树,最优候选路径即为最小生成树中包含起始点和目标点的最小子树,如图14中的蓝色曲线所示,即为最优候选路径由采样之后的锚点组成的路径。此时的路径虽然可以用于机器人的导航,但路径的代价和平滑度都不是最优的,需要进行调整。根据2.4节中的路径调整算法,对候选路径进行调整,这里障碍物代价和距离代价对应的权值系数μ取0.65,最终得到图14中红色曲线所示的调整后的最优路径。
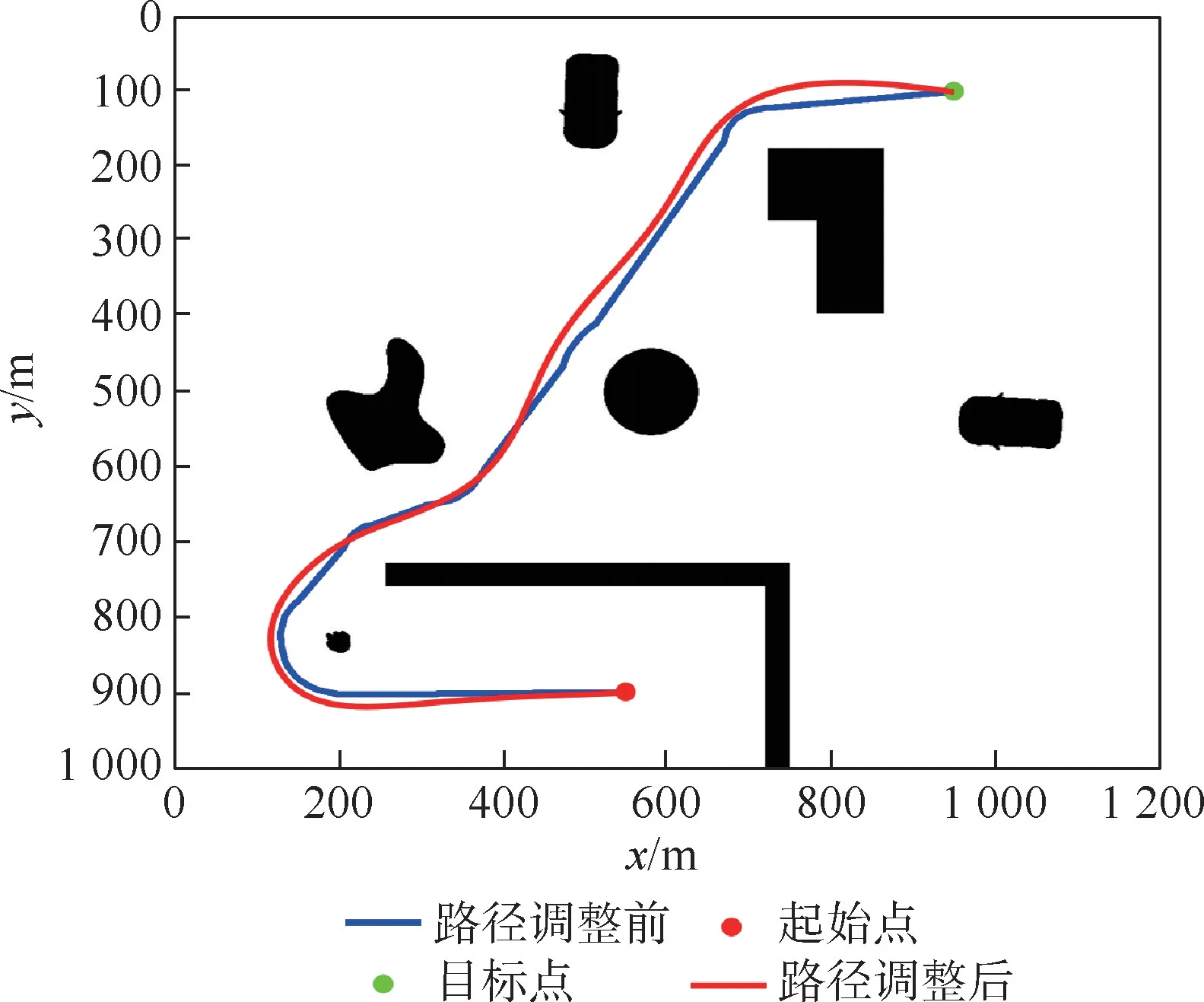
图14 静态障碍物场景中本文算法避障效果Fig.14 Obstacle avoidance effect of the proposed method instatic obstacle scene
3.2 动态场景下的避障分析
为了测试本文算法在动态场景下的性能,设定了如图15所示的动态障碍物场景。假设机器人从R点出发,目标点为G,其中A为移动的行人障碍物,B和C为2个移动的小车障碍物,在机器人避障的过程中其位置会发生变化。黑色的区域为静态障碍物。场景中的障碍物小车B和C及行人障碍物A运动轨迹为随机的曲线。在避障过程中动态障碍物的位置和速度会发生变化,因此,在生成动态障碍物的代价势场时需要考虑障碍物的速度大小和方向。按照2.4节提到的算法生成动态障碍物的速度代价势场,和静态地图的代价势场进行叠加,得到包含动态障碍物信息的代价势场。图16为按照第2节提出的路径生成和调整方案在实现动态避障过程中机器人与动态障碍物交互的仿真图。当机器人移动到图16(a)中位置时,动态障碍物代价势场及实时路径如图16(b)所示,当机器人移动到图16(c)中位置时,动态障碍物代价势场及实时路径如图16(d)所示。通过对比发现,机器人可以很好地根据障碍物的运动状态对当前局部路径进行调整,获得较好的避障效果。在动态障碍物场景下机器人避障路径及与动态障碍物的交互结果如图17所示,R为机器人的起始位置,G为机器人的当前目标点。图17展示了机器人及动态障碍物在运动过程中的运动轨迹,其中蓝色的路线为障碍物小车B的移动轨迹,黄色的路线为障碍物小车C的移动轨迹,橙色路径为行人障碍物A的移动轨迹。红色路径为机器人在避障过程中的运动轨迹,可以看出,在动态移动障碍物场景下机器人可以保持较为平滑的运动轨迹。图18展示了机器人在移动的过程中距离动态障碍物A、B、C及当前目标点G的实时距离,其中横坐标是移动机器人从起始点出发运行的时间,纵坐标是和动态障碍物之间的距离。由于在避障过程中引入了障碍物速度对代价势场的影响,在障碍物前进方向上的区域会产生对应的障碍物速度代价。可以看出,由于机器人在运动过程中通过障碍物速度可以考虑动态障碍物未来一段时间的位置对避障过程的影响,在移动障碍物场景下具有较高的灵活性。
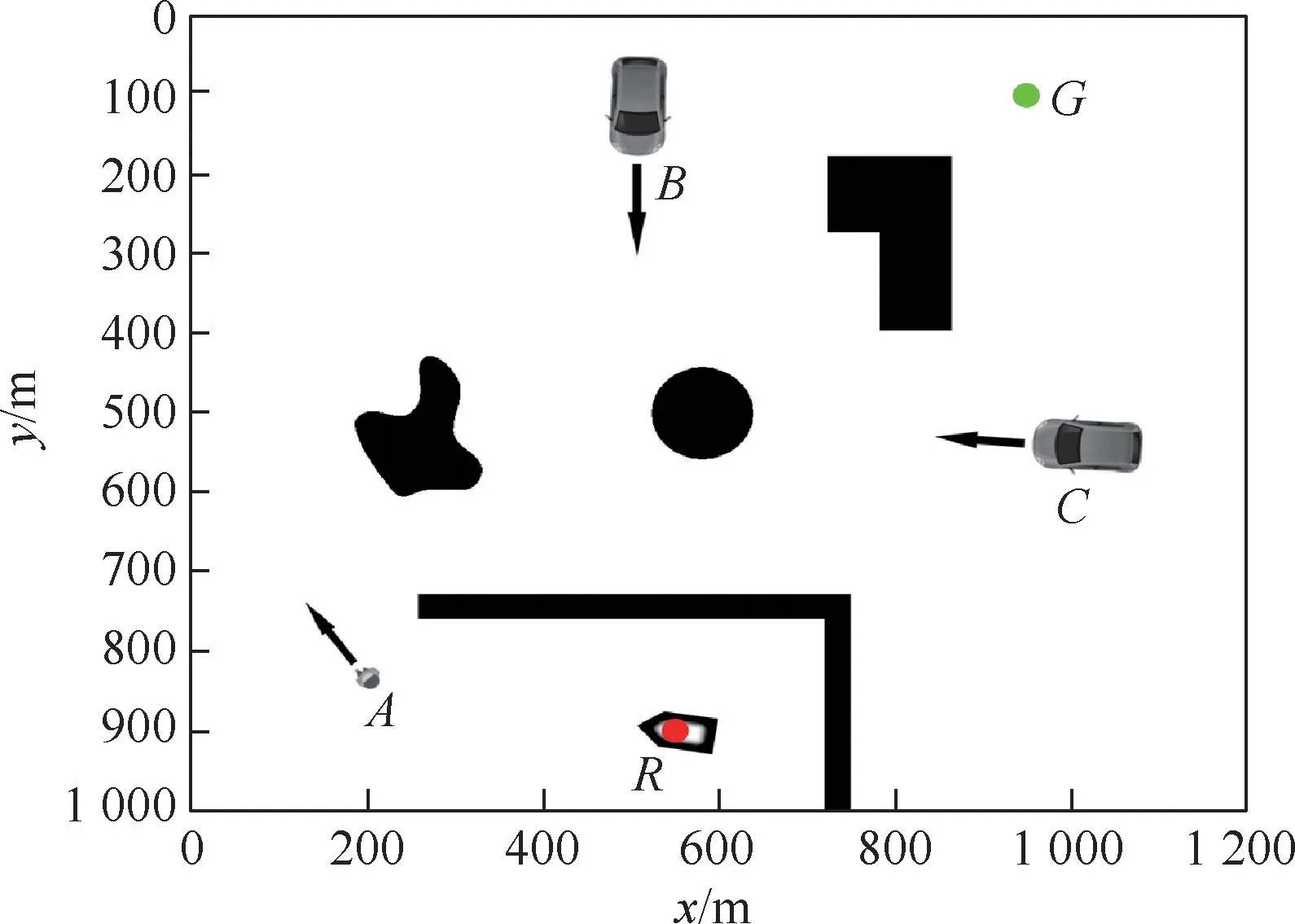
图15 初始动态场景中障碍物运动状态Fig.15 Obstacle motion state in initial dynamic scene
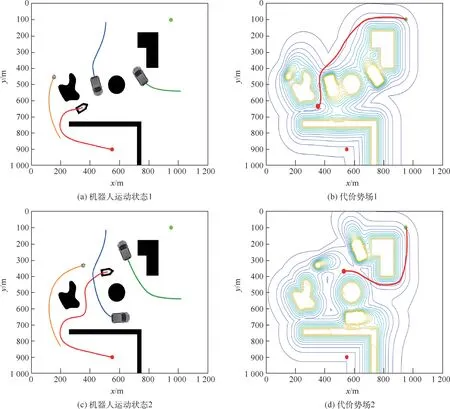
图16 动态场景中机器人实时避障路径Fig.16 Real-time obstacle avoidance path of robots in dynamic scenarios
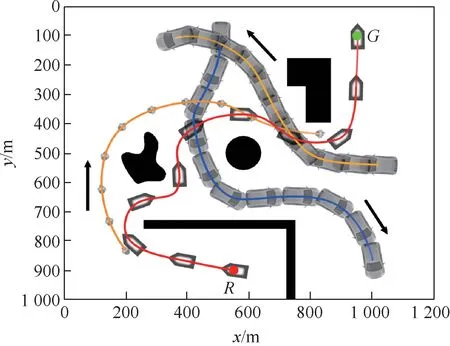
图17 机器人与动态障碍物交互过程中的运动轨迹Fig.17 Movement trajectory during interaction between robot and dynamic obstacles
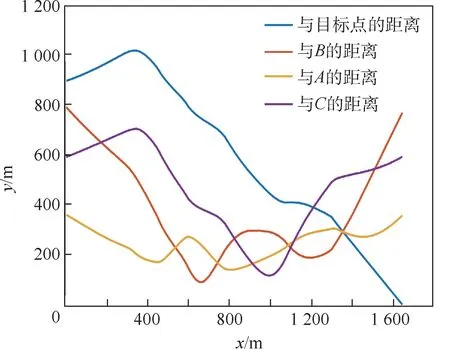
图18 机器人距离障碍物A、B、C及目标点的实时距离Fig.18 Real-time distance of robot from obstacles A,B,C and target point
3.3 不同算法的结果比较
本文提出了一种基于等势线和最小生成树的路径生成及代价势场下的路径调整算法。本节中,为了比较不同路径规划算法的特性和性能,构建了如图19所示的障碍物场景,对比了模拟人工势场(APF)算法、RRT*算法、A*算法和本文算法。为了方便不同算法搜索时间及搜索空间的对比,定义了地图遍历率的评价指标,其值定义为在完成1次路径规划过程中,栅格地图中被访问过的栅格数量与地图总栅格数量的比值,反映了算法的空间搜索效率。同时基于式(17)的路径评价指标,本文对比了4种算法在时间消耗及路径代价上的量化指标,如表1和表2所示,其中障碍物权值系数μ取0.40。
经典的APF算法[13]定义了2个主要的势场:引力势场和斥力势场。引力势场会吸引机器人向着目标点移动,障碍物产生的斥力势场会排斥机器人。最终机器人由受到的虚拟引力和虚拟斥力的合力牵引着向目标点移动,但是他也存在着一些缺点,如局部最优值问题和目标不可达问题。如图19中的绿色曲线所示,由于存在局部最优值,APF算法无法完成路径规划。当不存在局部最优值时,如图20所示障碍物场景,APF算法可以在人工势场中根据梯度下降法或邻域搜索法快速完成路径搜索,具有较高的时间效率及较低的地图遍历率,然而由表1和表2中的数据可知,由于没有考虑路径和障碍物间的距离及路径平滑度等因素,其路径具有较高的长度代价和加权代价,并不是最优的选择。RRT*算法[14]是以起始点为根节点,通过随机采样的算法增加叶子节点,生成一棵随机扩展树,当存在叶子节点进入目标区域,就得到了从起始点到目标点的路径。他的优点是实现较为简单,速度快,无论自由度多少,多复杂的约束都能适用。但缺点也非常明显,如图19和图20中的橙色曲线所示,由于其路径的随机生长方式,其生成的路径通常包含棱角,不够光滑,并且靠近障碍物,具有较高的时间代价和障碍物代价。根据RRT*算法中扩展树的随机生长方式,算法在执行过程中需要对整个地图空间内进行随机采样,会产生很多无效的栅格采样点,因此其地图遍历率较高。其路径规划参数对比如表1和表2所示,其路径长度代价和障碍物代价都相对较高,并且不是最优的。
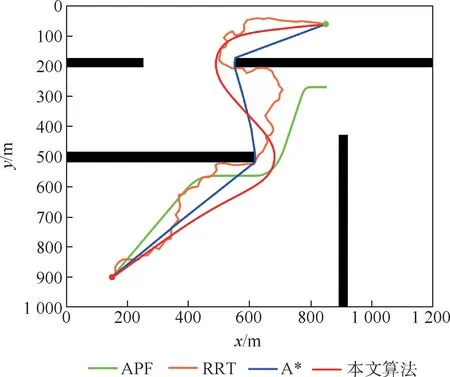
图19 场景1中不同算法的路径规划结果对比Fig.19 Comparison of path planning results of different methods in Scenario1
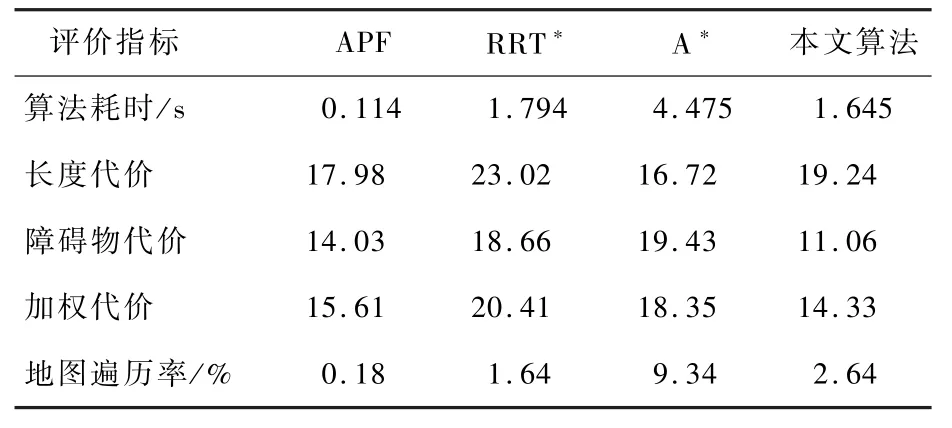
表1 场景1中不同算法路径代价指标的10次平均值对比Table1 Ten mean comparison of path cost indexes of different methods in Scenario1
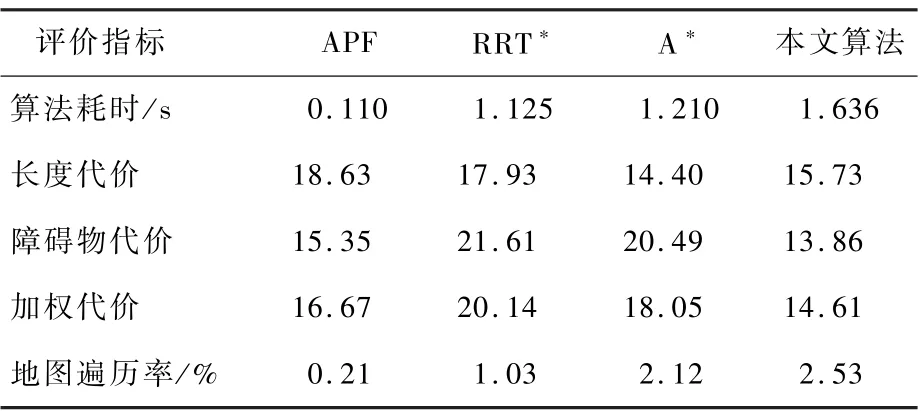
表2 场景2中不同算法路径代价指标的10次平均值对比Table2 Ten mean comparison of path cost indexes of different methods in Scenario2
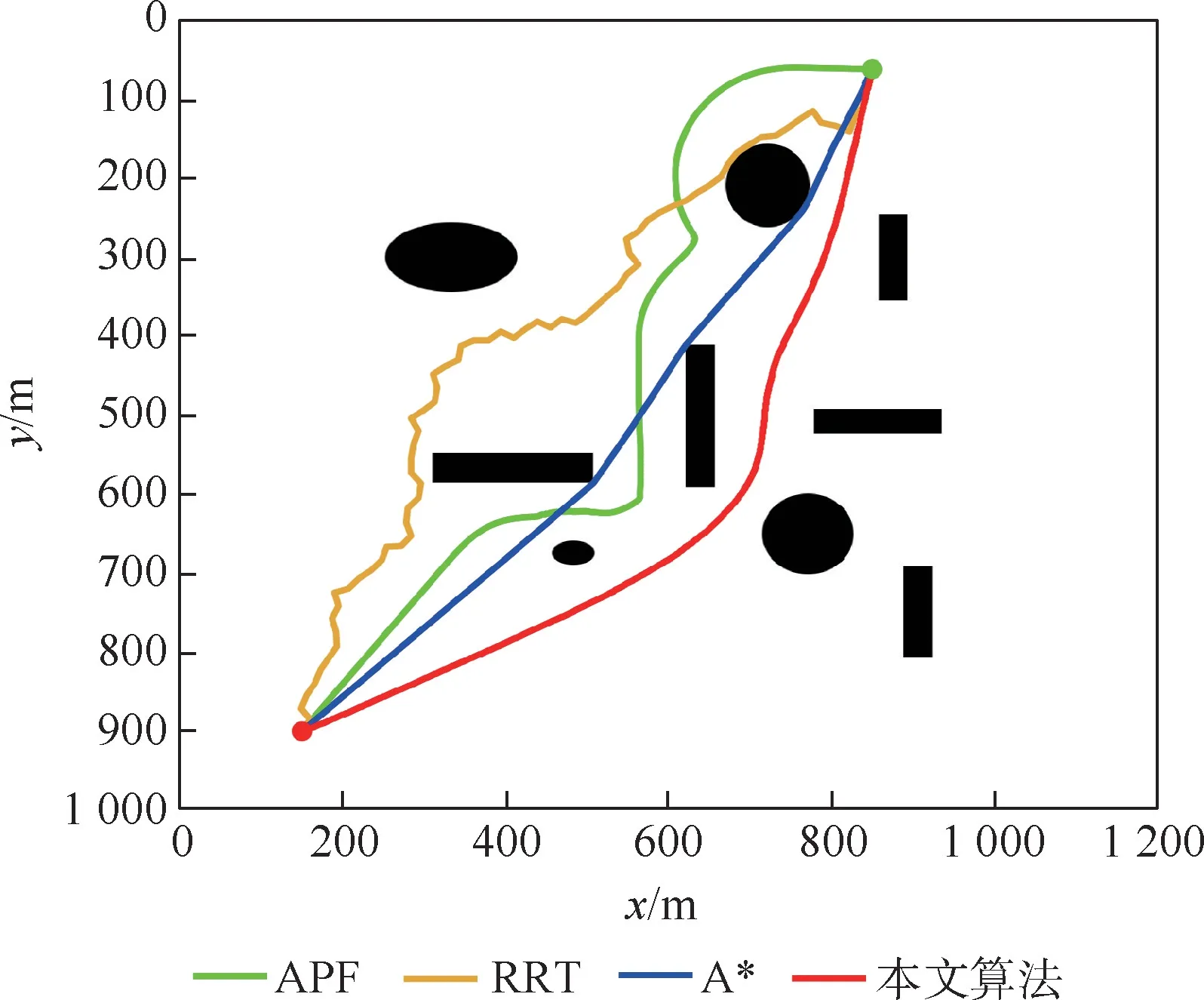
图20 场景2中不同算法的路径规划结果对比Fig.20 Comparison of path planning results of different methods in Scenario1
A*算法[15]的显著特点是基于栅格地图完成路径的搜索,由起点开始,每次优先选择距离起点代价和距离终点的预计代价之和最小的节点作为下一个要遍历的节点依次遍历,直到到达终点。A*算法没有考虑和障碍物的安全距离,并且生成的路径不够平滑,如图19和图20中的蓝色曲线所示。在实际应用过程中需要进行进一步的优化。在目标点被障碍物遮挡且地图分辨率较高的栅格地图场景中,A*算法会有大量的无效节点栅格被加入有效点集合,因此搜索过程中花较多的时间查找有效点集合,仿真中耗时高于另外3种算法,并且具有较高的地图遍历率,同时路径的障碍物代价值也相对较高,在实际过程中很容易与障碍物发生碰撞。当目标点不被障碍物遮挡或存在较少的障碍物遮挡时,如图20所示仿真场景,算法的地图遍历率和耗时相比图19仿真场景有所降低。APF的时间复杂度相对较低,并且具有较小的障碍物代价值,但由于其存在局部最优问题,在存在局部最优值的场景中无法完成避障任务。RRT*算法采用概率随机树的方式生成避障路径,也存在障碍物代价高的问题,并且由于树的生长方式是随机的,在相同的场景下每次的时间消耗和障碍物代价都可能发生变化。由表3的数据可知,RRT*算法在相同场景下进行多次的路径规划仿真时,算法的长度代价方差与障碍物代价方差都比较大,得到的路径具有随机性,这对于移动机器人的动态避障是不利的,相比之下APF、A*及本文算法在多次重复实验时差较小,具有较高的稳定性。本文算法同时考虑了路径长度,障碍物代价,路径平滑度等多种因素,通过求解代价势场等势线切点和求解最小生成子树的方式获得初始路径,假设锚点间存在引力,并且会受到代价势场的影响,通过调整路径锚点获得有效路径,由表1和表2的数据可知,本文算法在时间复杂度和障碍物代价值上都具有较好的指标,同时也具有良好的地图遍历率指标。

表3 场景2中不同算法路径代价方差对比Table3 Variance comparison of path costs of different methods in Scenario2
3.4 复杂场景下的自主避障
本节测试了在相对较为复杂的场景下本文算法的避障效果,并对比了APF算法、A*算法和本文算法的不同表现,栅格地图的大小同样是1200×1000m,如图21所示,黑色栅格区域为障碍物,红色点(300,900)为起始点,绿色点(900,60)为目标点。选择高度为hc=120的等势线可以在代价势场中得到图22红色曲线所示的初始候选路径。为了方便比较,地图中没有设置局部最优值,保证了APF算法也能够完成避障。

图21 复杂场景下的避障结果对比Fig.21 Comparison of obstacle avoidance results in complex scenarios
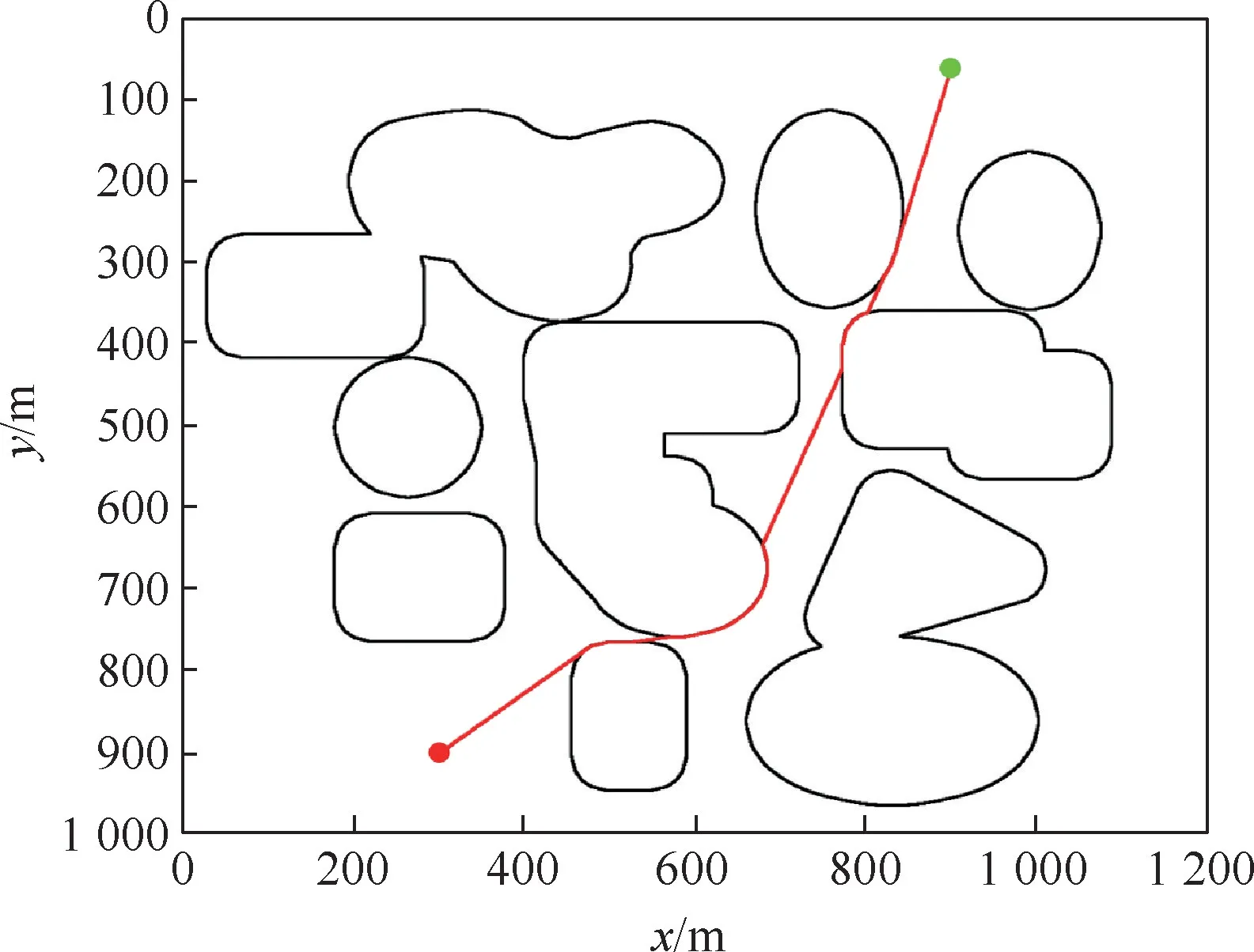
图22 基于等势曲线生成的初始候选路径Fig.22 Initial candidate path generated based on equipotential curve
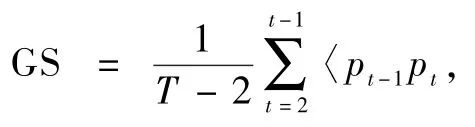
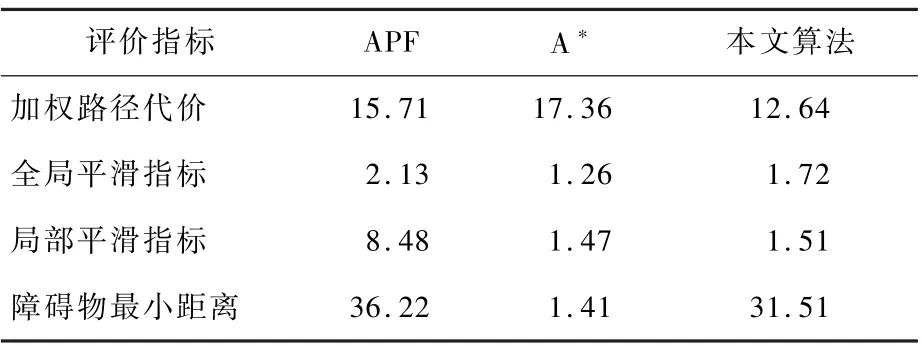
表4 不同算法评价指标的10次平均值对比Table4 Ten average comparison of cost indexes of different methods
实验结果表明,本文算法通过对候选路径在路径长度和障碍物代价上的调整,得到的路径具有较好的平滑性和安全性,同时加权路径代价也相对较小。
4 结 论
针对动态障碍物场景下的移动机器人安全避障问题,本文提出了基于障碍物代价势场的避障路径生成及调整算法,并进行了仿真验证。
1)本文所提算法可以得到较为平滑的路径,能够在和障碍物保持安全距离的前提下做到路径最短。在静态场景下,如果障碍物本身的位置不会发生变化,通过所提算法动态的生成可行路径,并在机器人不断运行的过程中对路径进行调整,可以获得可靠的导航和避障结果。
2)对于移动的障碍物,所提算法加入了其移动速度对障碍物代价势场的影响,在障碍物前进方向的区域范围内产生较强的代价势场,为机器人规避移动中的障碍物预留了充分的裕量,使得机器人可以对障碍物未来的运动态势进行一定程度的预测,对于移动中的障碍物也能够达到较好的响应效果。
3)所提算法综合考虑了路径的长度和障碍物代价,相比其他算法,在路径平滑指标、长度代价等单一指标上不是最优的,但是通过所提算法对路径的调整使路径具有较好的安全性及较小的加权代价,有利于实际应用中实现良好的路径跟踪和避障。
