基于GA-SVR的城市交通运输碳排放预测研究

高金贺， 郑宝珠， 周伟昊， 李 鹏

(东华理工大学 土木与建筑工程学院，江西 南昌 330013)

目前，在研究城市交通运输领域的碳排放问题时，通常关注影响因素分析和节能减排预测两大类。如在影响因素方面，陈亮等(2017)对STIRPAT模型进行改进，针对其中的主要影响因素开展全面的分析且进行整体排序；Lin等(2009)基于IPAT模型增加了能源与城市化率2个影响因素指标，而且还利用STIRPAT模型来深入探讨各个指标所带来的影响；武翠芳等(2015)则是以STIRPAT模型为基础来探讨了从1999年到2011年吉林省的碳排放数据，对交通能源利用过程开展全面的分析，并且根据所得的结果提出了相应的建议。多数研究人员主要针对影响因素和碳排放二者之间的关联性，构建IPAT、Kaya等式或者GM(1，1)模型，从而对交通运输碳排放总量进行准确预测(聂锐等，2010；Waggoner et al.，2002；Shahbaz et al.，2015；胡茂峰等，2022)。

然而，传统的预测方法存在回归不稳定、影响因素不确定等一些问题，从而会降低预测的科学性和准确性。对于复杂的非线性预测系统来说，如果训练和测试的样本不足，将会产生误差，并且烦琐的计算过程也会使得最终计算精度降低(陈亮等，2018)。

综上所述，笔者通过分析STIRPAT模型中各个因素，选择了7项城市发展的重要指标数据作为基础因素；同时，为了减少传统预测误差，通过构建遗GA-SVR模型来预测北京市交运领域的碳排放量，并进行深入讨论。

1 影响因素选取与模型建立

1.1 碳排放影响因素选取

STIRPAT模型是York等(2003)基于回归方法考察各类因素对城市环境和交通碳排放的随机影响模型，并且其模型指标的选取可以根据地区实时状况进行拓展改进。根据现有规范和前人研究的成果可知，城市交通运输行业碳排放主要影响因素包括内部发展模式方向、对外交流发展水平和城市环境变化3个方面(陈亮等，2017；宋杰鲲，2012),因此选择人口总量、人均GDP、机动车保有量、旅客周转量、货物周转量、城镇化率和碳排放强度作为影响因素指标。其中人口与人均GDP能够反映出城市发展方向，机动车保有量、旅客周转量和货物周转量代表了城市对外交流的发展水平，城镇化率和碳排放强度则代表了城区的环境变化等因素。

碳排放强度是反映经济增长速度的指标之一，其公式为：

(1)

式中，I为碳排放强度(t/万元)，Pt为交通行业碳排放量(t)，Gt代表地区生产总值(万元)。

1.2 预测模型建立

1.2.1 遗传算法基本原理

河南尉氏县及商丘、周口一带流传的一则关于腊八粥的传说，把腊八节食粥习俗与我国古代思想家、教育家孔子结合起来，由此把腊八食粥俗的起源推至春秋时代，与史书记载相差甚远。传说孔子带领72门徒周游列国。这天，他们来到陈蔡坡被困到弦歌台，师徒疲惫不堪，人无食充饥，马无草喂养。孔子思虑再三，嘱子路和冉求到西山找范丹老祖借点粮草。二人走了几天，在一座山神庙里，见到一位老人。老人蓬头垢面，破衣烂衫，脚踏藤条捆绑的烂鞋，庙内空空荡荡。两人上前询问，果然是范丹老祖。老祖看过孔子的信，上下打量子路和冉求，冷冷地说道：“看你老夫子的脸面，我出道题，若答得出，就借给你们粮草，若答不出，就啥也别想。”

遗传算法主要被用来模拟在自然选择以及遗传过程中所存在的各类生物现象，如基因突变、染色体交叉以及繁殖等(刘志强等，2013)，它们会在遗传进化之后形成新种群个体来作为相应的候选解，再按照适应度函数即选择指标从这些候选解中选取适应度较优的个体，根据遗传算子在选择、交叉或突变后再次产生新的候选解群，重复上述过程最终得到收敛指标。遗传算法可以在众多解决方案中搜寻出最佳方案，并且可以减少陷入局部最优解的风险，可有效保证全局最优解的选取。

1.2.2 支持向量机基本原理

支持向量机最先由Vapnik团队提出，它主要基于线性可分最优超平面而逐步发展而成(邓乃扬等，2009)，其核心思想是使用核函数为高维原始样本的映像构造一个最优超平面(秦耀祖等，2021)，如图1所示。图中不同形状的点(圆圈和方框)分别代表不同的样本集，H为两类不同点的分界线，H1和H2分别为经过两类不同样本且到分界线距离最近的两条不同直线；在支持向量机中，将使得H1到H2之间的距离为最小的距离时称之为分类间隔，使得间隔最大时的超平面称为最优超平面H。二维线性分类中，H、H1、H2的方程可表示为：

(2)

式中，w为H方程的斜率，x为因变量，b为常数。

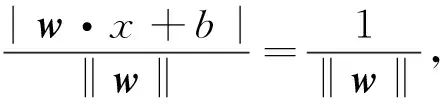
(3)

采用Lagrange函数按乘子求解法转为对偶函数得到最优超平面分类函数：

(4)

f(x)=sgn{w*·x+b*}

(5)

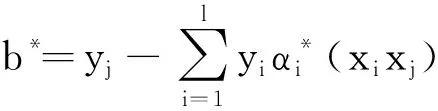
当训练集线性不可分时，引入惩罚因子C和松弛变量ξi≥0，i=0,…,l，再引入非线性映射函数φ，使目标函数变为最小：

(6)

训练算法使用特征空间中的内积φ(xi)φ(xj)，并引入核函数K(xi,xj)=φ(xi)φ(xj)，使其实现非线性到线性分类的转换。本次主要研究径向基核函数K(xi,xj)=exp(-g‖xi-xj‖2)，其中g为核函数参数。

1.2.3 算法实现

目前，支持向量机已经被大量地应用于多分类领域中(Smola et al.，2004；Kennedy et al.，1997)，但影响城市交通运输碳排放的因素较多，且各影响因素之间有一定的重叠性和相关性，仅用原始的支持向量机进行预测会对结果产生不利影响(解少博等，2013；卢建中等，2015；李松等，2012)。而基于遗传算法优化支持向量机模型可通过先测试惩罚参数C、核函数参数g等参数的最优解，解决被检测事件的错误率；再利用该方式训练支持向量机，训练和测试结果的相关系数和均方误差较单独使用支持向量机的结果更加精确。因此，将遗传算法与支持向量机相结合，建立用于预测城市交通碳排放的GA-SVR模型。具体步骤如图2，取模型预测准确率作为遗传算法(GA)中的适应度函数值。

2 数据来源与实例分析

2.1 数据来源

以北京市的基础数据进行实例分析，数据均来自历年《北京市统计年鉴》，样本时间为1995—2019年，收集了人口数、城镇化率、货物周转量和碳排放强度等7项影响因素，如表1所示。

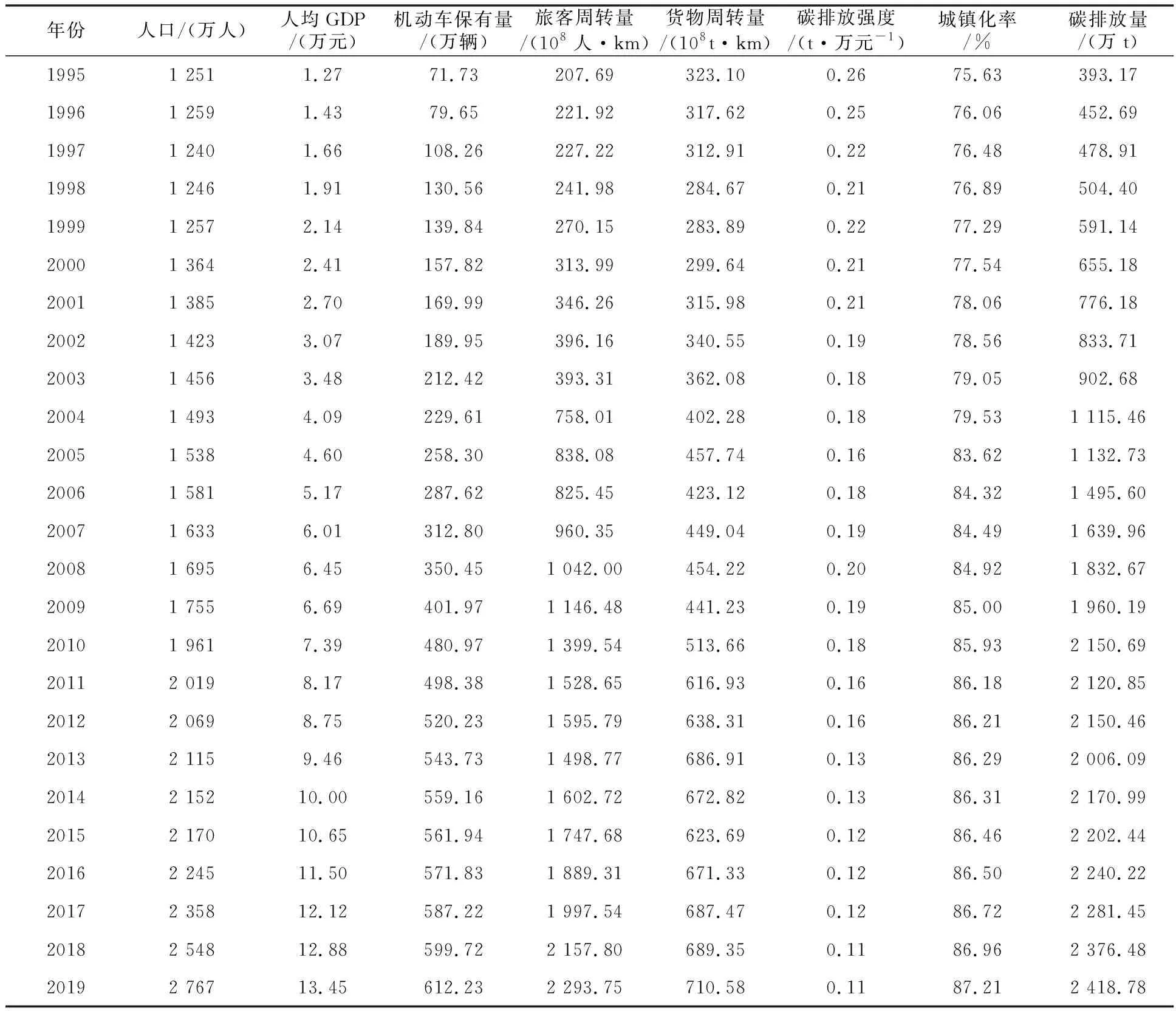
表1 交通运输碳排放及其影响因素数据

2.2 MATLAB运行结果及回归分析

依据GA-SVR预测模型的基本流程，采用前十二年的相关数据来构建训练集，再以此后的十三年数据作为该模型所需的测试集。在本研究中，最大的种群数量为默认值20，而最大进化代数的值则为200，参数C的变化范围取默认范围(0,100)，参数g的变化范围取默认范围(0,100)，经过GA算法优化计算后，得到的最优惩罚参数C和g分别为94.946 5和0.005 340 6，均方误差(MSE)为0.032 756，图3为GA优化的适应度曲线变化图。

按预测过程处理分析训练集和测试集数据，得到回归值与真实值对比，如图4所示。其中，训练回归方程为Q=1.030 3M-10.905 7，相关系数为0.982 81，MSE为 0.007 162； 测试回归方程为Q=1.037 4M-46.043 4，相关系数为0.962 42，MSE为0.007 470。变量M为原始碳排放量(万t)，变量Q为预测碳排放量(万t)。

在图5中，详细列出了预测值和真实值之间的比较结果，此时该算法对训练集和测试集的平均回归精度达到了95%以上，可为城市交通碳排放数据进行较为准确的预测。

2.3 未来城市碳排放预测

2.3.1 影响因素预测分析

根据北京市各项统计数据及历史年鉴，深入探讨从2020年到2023年该领域碳排放指标的主要影响因素，根据样本数据可确定各影响因素年平均增长率，预测2020—2023年间北京市各影响因素值如表2所示。

表2 2020—2023年间各影响因素预测值

2.3.2 碳排放预测分析

将2020—2023年交通运输碳排放7项影响因素预测值归一化后带入模型中，得到北京市的交通运输碳排放预测值。由表3预测结果可知，碳排放量仍将逐年提高，说明随着时间的推移，减少碳排放量依旧刻不容缓。因此，北京市应控制人口和机动车保有量等指标的增长；此外，还应当大力普及清洁燃料，研究新型的节能减排工艺技术，并逐渐实现实用化，适当增加对新能源车辆的使用；与此同时，合理安排绿色出行结构，积极向低碳化方面发展，提高交通运输的科技水平。

表3 交通运输碳排放预测值

3 结语

(1)利用遗传算法对支持向量机进行优化，建立城市交通碳排放的GA-SVR预测模型。运用模型得到的GA-SVR均方误差为0.032 756，训练集拟合的相关系数和均方误差分别为0.982 81和0.007 162，测试集拟合的相关系数和均方误差分别为0.962 42和0.007 470，训练集和测试集的平均精度达到了95%以上。

(2)通过预测结果可知，城市交通运输碳排放量依旧呈上升趋势，到2022年既有可能突破2 500万t，人口和机动车保有量等指标的增长将会进一步引起城市交通运输碳排放量的增长。城市交通仍面临较大环境压力，故北京市不仅应该加大绿色公共交通数量投入，还需要进一步推广节能减排与清洁燃料等方面的技术成果。