砂岩型铀矿溶质迁移的数学模型及数值算法

张 文, 丁子荣, 沈 启, 王海涛， 阮周生

(1.东华理工大学 理学院,江西 南昌 330013; 2.合肥铁路工程学校,安徽 合肥 230000;3.东华理工大学 核应用技术研究所,江西 南昌 330013)

砂岩型铀矿是我国主要的铀矿床类型之一，研究深部砂岩型铀矿原地浸出的溶质迁移渗流规律，对于丰富和提高地浸采铀的基础理论认识和技术发展具有重要的理论意义与应用价值。

由于砂岩型铀矿储层的渗透系数较低，导致固液及液液界面的作用力较大，溶浸液很难迁移渗流。针对低渗透多孔介质渗流理论方面，许多学者开展了不同程度的研究并取得了一定成果(Mudd，2001；魏恒等，2013；阙为民等，2002；尹升华等，2006，2008，2013；李超等，2007；曾晟等，2011；Mellado et al.，2009；赵贺永，2015；李衡等，2019；Zhang et al.,2016；焦养泉等，2020；何润发等，2020)。溶质在多孔介质中的迁移一般以对流与机械扩散为主，基于Fick扩散定律的对流扩散方程是描述溶质运移行为模式的经典模型(Zheng et al.，2002)，即溶质浓度在迁移过程中满足的动力学模型为：

(1)

式中，u(x,t)表示在空间位置x处、t时刻的溶质浓度，k为扩散系数(k>0)，v为对流系数(v>0)，f(x,t)为源项，f(x,t)>0时为源，f(x,t)<0时则为汇。然而，用对流扩散方程模型来描述溶质的运移过程时，并不能很好地模拟穿透曲线的提前穿透或拖尾现象。若用微观粒子的扩散过程来解释这种不足，则表现为Fick定理描述的是微观粒子向相邻一个单位空间的扩散，但是在各向异性多孔介质中，微观粒子的扩散可能向相邻多个单位空间扩散。从随机过程的角度去看，经典扩散为微观粒子的局域性运动，是中心极限定理的直接结果，迁移过程遵守Fick定律，统计规律表现为均方位移与时间呈线性依赖关系；反常扩散现象表现为微观粒子的非局域性(时间和空间)运动，是一种复杂系统的扩散过程，迁移过程不再遵守Fick定律，均方位移与时间呈现出非线性的依赖关系。描述反常扩散现象的方法和模型主要有分数布朗运动、广义的扩散方程、连续时间随机游走模型等。近年来，在很多复杂系统中均观察到这种反常现象，如金融市场以及多孔介质中的扩散等(张继伟，2021；Podlubny,1999)。

针对不满足布朗运动的反常扩散行为，通过Eulerian推导提出分数阶Fick定理(Schumer et al.，2001)。在此基础上，关于流体在多孔介质中迁移的分数阶对流扩散方程也被推导出来，其能够很好地描述分形几何、幂律现象及记忆过程等反常扩散现象(Wheatcraft et al.，2008)。由于分数阶微积分适合描述反常扩散过程，在各种科学和工程领域得到了关注，但其非局部性质的缺点导致很难计算出分数微分方程的解析解，于是寻求更简单高效的数值方法来求解分数阶微分方程成为众多学者研究分数阶微分方程的核心问题之一。笔者结合Caputo-Fabrizio时间分数阶导数与对流扩散方程，研究深部砂岩型铀矿地浸过程中溶质迁移的数学模型与数值解法。

1 数学模型

假设含铀溶液的浓度u(x,y,z,t)是一个与三维空间(x,y,z)和时间都有关的量，考虑含铀溶液在砂岩型铀矿地浸迁移的机理。根据质量守恒定律，小区域中浓度变化由物质流入流出引起，用连续性方程的微分形式表示为：

(2)

F=-ku

(3)

(4)

当考虑流体中的静水压力时，由外力、重力、浮力、毛细管力等共同作用引起的压力差会导致流体介质整体的流动，对浓度变化也将做出通量贡献。根据质量守恒定律可得对流扩散方程：

(5)

(6)

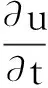
(7)

为使得表达形式更为简洁，考虑空间方向为一维形式，则：

(8)

(9)

(10)

2 时间分数阶导数的数值计算

2.1 Caputo-Fabrizio时间分数阶导数的计算格式

根据Caputo-Fabrizio导数的定义(Caputo et al.，2016)

(11)

式中，a表示区间[a,t]的起始端点满足相容性条件，即：

当α→0+时有：

(12)

以及当α→1-时有：

(13)

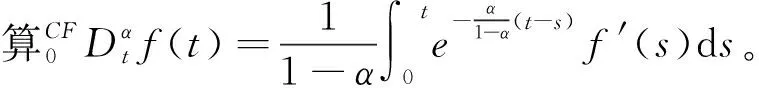
(14)

令

(15)

(16)

(17)

(18)

令

(19)

易知hj-i(t)为一个r次多项式，且满足关系

(20)

于是有

(21)

令

(22)

(23)

则

(24)

(25)

且逼近误差为：

(26)

(27)

[f(t0)，f(t1)，…，f(tr-1)]T

(28)

[f(t0)，f(t1)，…，f(tn)]T

(29)

于是有

(30)

若记系数矩阵

In·Ωn,r=Gn=(gn,gn-1,…,g0)(n+1)

(31)

(32)

其中

2.2 Caputo-Fabrizio时间分数阶导数的数值模拟

为了直观展示分数阶导数数值计算格式(32)的精确性，有利与Li等(2016)的计算结果进行比较，下述2个算例函数均选自Li等(2016)。不同的是， Li等(2016)中讨论的为奇异核函数(t-s)-α分数阶导数，采用了更为复杂的4次或5次多项式以达到4阶或5阶精度。

算例1，选取函数f1(t)=t6，易知分数阶导数的精确解为：

算例2，选取函数f2(t)=e2t-2t-2t2-

表1和表2分别给出了算例1和算例2的计算误差和数值精度。以上2个算例表明，选取2次或3次Lagrange插值多项式进行逼近时，能达到3阶或4阶精度，因此在进行Caputo-Fabrizio时间分数阶导数对流扩散方程初边值问题的数值模拟时，采用2次Lagrange插值多项式进行模拟。

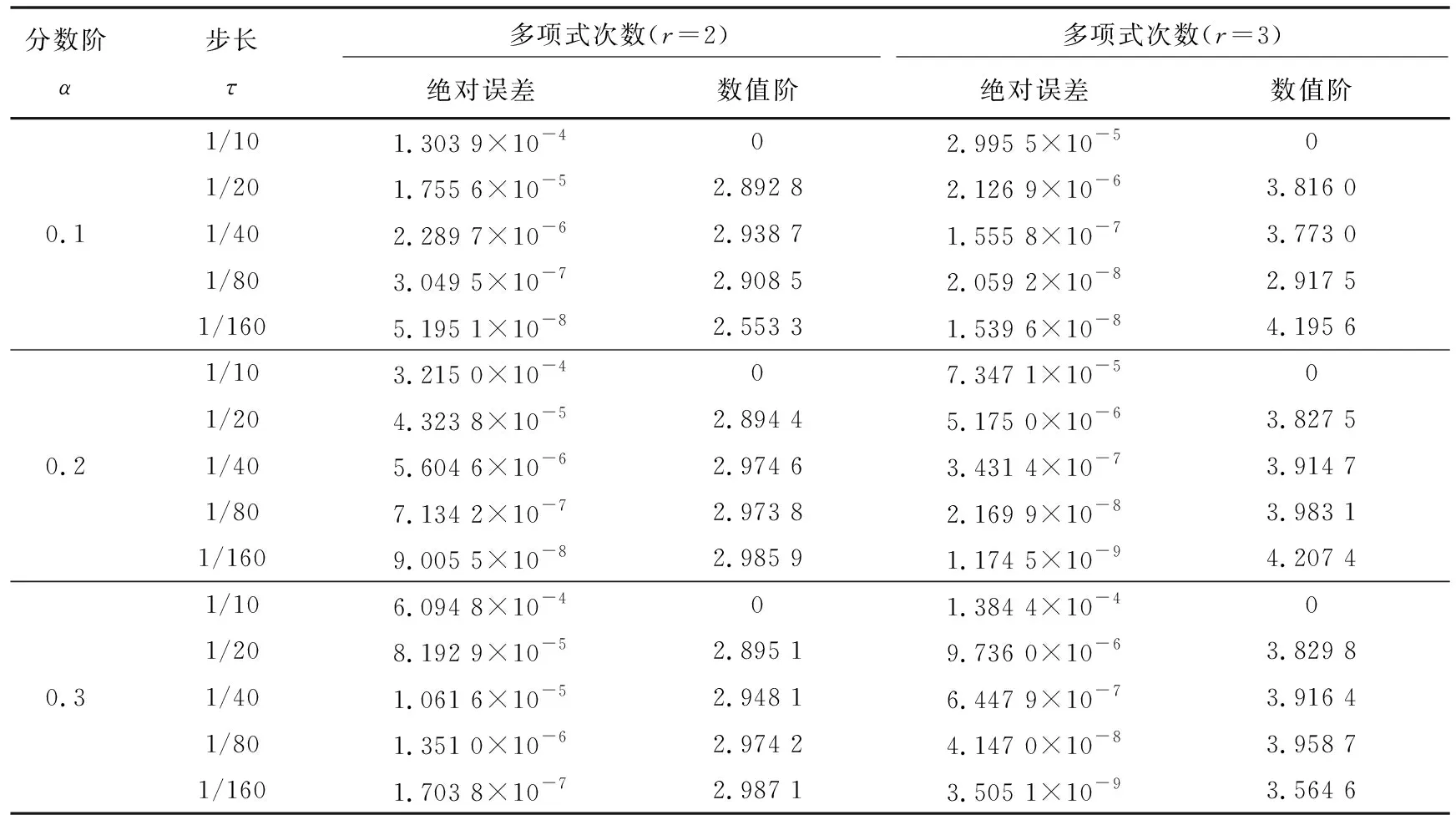
表1 算例1的数值结果

续表

表2 算例2数值结果

3 数学模型在地浸采铀中的应用

将分数阶导数的计算格式嵌入式(10)得出数学模型(10)的计算格式，并应用于我国西部某铀矿采冶区，结合铀矿采冶区的探测数据，进一步验证数学模型(10)的有效性。

3.1 溶质迁移数学模型的离散格式

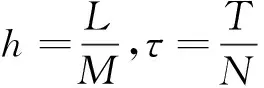
(33)

(34)

于是，式(10)中第一个方程的数值计算格式可表示为：

(35)

式中，

初始条件(m=0,1,…,M)：

(36)

边界条件(n=0,1,…,N)：

(37)

最终，式(10)的离散数值格式为:

(38)

整理后便有(m=1,2,…,M-1,n=1,2,…,N-1)：

(39)

其矩阵形式为：

HU=F

(40)

式中，

由求解三对角方程的追赶法易解出U，进一步便能逐层求解出un(n=0,1,2,…,N)。

3.2 数学模型砂岩型铀矿地浸中的应用

根据国际原子能机构的统计数据(World Nuclear Association，2021)，原位浸出模式(图1)已在铀矿开采中广泛使用，如加拿大的麦克阿瑟河铀矿、哈萨克斯坦的特尔库特蒙库姆铀矿以及澳大利亚的奥林匹克坝铀矿。适合原位浸出模式的矿床通常具有2个特点:①具有一定渗透性的疏松砂岩型铀矿床；②矿层上、下层具有较稳定的顶、底板隔水层。目前，地浸采铀技术主要有酸法浸出和碱法浸出。以美国为首的西方国家基本采用以二氧化碳和氧气为体系的碱法浸出工艺，俄罗斯、哈萨克斯坦等国家基本采用以硫酸为体系的酸法浸出工艺，我国根据砂岩型铀矿不同的矿床地质与水文地质条件来选择酸法或碱法浸出工艺。

我国西部某砂岩型铀矿采冶区采用以硫酸为体系的酸法浸出工艺，在注液井和抽液井之间放置中子测井仪，可以获取矿体中的剩余铀含量的监测数据。为方便对监测数据进行了归一化处理，下面通过式(10)模拟在一维空间下铀元素的迁移过程。

选取源项函数：

(41)

则易知式(10)所对应的精确解为u(x,t)=exsinx,φ(x)=0,φ(t)=sint,ψ(t)=e·sint。根据监测数据估计出环境参数: 分数阶α为0.001，扩散系数k为10-8和对流系数v为10-6。

通过计算数值解与精确解的相对误差:

可以看出，数值格式(40)计算稳定、精度高，该数学模型能较好地模拟原位浸出问题。

4 结论

基于含铀溶液在砂岩型铀矿地浸迁移的机理，建立了溶质迁移的时间分数阶对流扩散方程数学模型，利用数值方法推导了Caputo-Fabrizio分数阶导数对流扩散方程精度较高的数值格式，并通过算例验证了格式的高精度和高效率。将所建立的数学模型应用于我国西部某砂岩型铀矿地浸采铀中，结果显示数学模型是可靠的、数值算法是高效的。由于监测井孔代价高昂，监测数据非常有限，导致反演环境参数(分数阶α、扩散系数k和对流系数v)并不理想，下一步课题组将引进正则化等方法，针对如何准确反演环境参数、预测剩余铀含量等方面展开研究。