基于遗传算法的榫槽部位模拟件设计方法

2022-11-28张志佾王佰智张峻峰

航空发动机 2022年5期

艾兴，叶璇，李坚，张志佾，王佰智，张峻峰

（1.中国航发湖南动力机械研究所，湖南株洲 412002；2.中国航空发动机研究院，北京 101304）

0 引言

在航空发动机零部件上具有多个几何不连续部位，通常这些部位存在应力集中，在高温、高压和高转速等高负荷疲劳载荷下，均可能发生疲劳失效，严重影响航空发动机的结构完整性[1]。关键零部件的疲劳试验和寿命评估是航空发动机零部件安全性和可靠性评价的重要研究内容，但这些零部件存在制造成本高、考核部位多、试验系统复杂、试验费用昂贵等问题。在航空发动机零部件寿命评估方法及试验考核局部应力状态方面，开展能反映真实构件局部应力状态的模拟件疲劳试验，并根据少量的真实构件疲劳试验数据验证模拟件设计的准确性。真实构件的模拟件试验可以弥补零部件试验成本高、试验件少的不足，具有重要的工程价值[1]。榫槽部位是航空发动机关键部位，几何特征较为复杂，应力较高，在结构强度评估中需要重点关注。

近年来，国内外学者针对航空发动机榫接部位特征模拟件设计方法进行了研究。针对航空发动机涡轮叶片榫头部位疲劳试验，Issler等[2]设计出了能够表征涡轮叶片服役状态时的模拟件，其应力分布与涡轮叶片服役时的相似；Ruiz等[3]在25T双轴疲劳试验机的基础上设计了相应的模拟试验件和夹具，通过横、纵双向加载，实现了轮盘榫连接结构的模拟；黄致建等[4]在单轴疲劳试验的基础上设计了可反映真实工况的燕尾形榫连接结构的微动疲劳模拟试验件及加载夹具，开发了变摩擦系数的接触边界元计算程序，可快速计算等厚度盘燕尾形榫头/榫槽接触区域的应力分布；陆山等[5]提出了基于任意最大应力梯度路径的轮盘模拟件优化设计方法；刘廷毅等[1]、由美雁等[6]、杨兴宇等[7]针对不同零部件的结构特征设计了不同类型的模拟件。

上述研究表明，榫头/榫槽部位模拟件设计大多仅考虑了特征部位最危险点的应力或应变，而忽略了特征部位应力梯度的影响，导致模拟件的试验寿命无法反映真实情况。在进行模拟件设计时，如果只依靠设计者的经验或者采用试凑的方法，将会使设计工作量大增，不但不能获得最优解，甚至最终导致设计失败[8-9]。在优化算法中遗传算法具有简单通用，鲁棒性好，可获得全局优化解等优点。因此，本文将遗传优化算法与商用有限元软件Abaqus相结合，提出了考虑了应力梯度影响的航空发动机榫头/榫槽特征部位模拟件设计方法。

1 模拟件设计原则

在进行模拟件设计时，需要考虑材料制备等工艺引起的初始损伤、结构特征所产生的应力梯度及温度梯度等带来的影响。一般需要遵循以下原则：

（1）模拟件要与零部件材料及其性能保持一致；

（2）模拟件试验温度载荷条件与零部件服役温度载荷条件相同；

（3）模拟件应力最大值相同，且应力最大值对应的点附近一定区域内的应力梯度分布与零部件相同。

2 模拟试验件优化目标获取

2.1 危险点第1主应力方向

利用文献[5]获取应力梯度路径的方法，对工程零部件进行疲劳分析时，可将第1主应力最大位置作为零部件的危险位置（即裂纹萌生点），裂纹开裂面与裂纹萌生点第1主应力方向垂直，裂纹沿尖端第1主应力垂直方向扩展，扩展轨迹在3维空间中呈一曲面。为了获得裂纹扩展轨迹，需要对裂纹尖端第1主应力的方向求解。

结合商业有限元软件分析零部件在真实载荷条件下的应力分布情况，获得零部件任意位置处的各应力分量分别为σx、σy、σz、τxy、τxz、τyz，第1主应力σ1对应的应力方向分别为l1、m1、n1，任意1点处的3维应力状态如图1所示。根据弹性力学的平衡方程和余弦关系依次可求得l1、m1、n1，从而确定第1主应力方向。

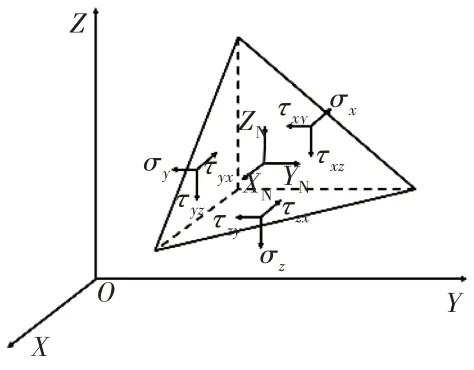
图1 任意1点处应力状态

2.2 第1主应力梯度路径

以垂直于危险点第1主应力方向（l1、m1、n1）的法向平面为裂纹扩展危险截面。第1主应力梯度路径获取方法如下：以O点为圆心，以固定长度Δr为半径步长分别绘制一系列圆，找出特征点（每个圆上最小主应力点），将这些特征点连线，获得零部件危险部位最大第1主应力梯度路径P0Pn

[5]，如图2所示。零部件的裂纹扩展行为受该平面上应力状态的影响，该曲线可近似表征零部件危险点裂纹扩展轨迹。

图2 零部件危险部位最大第1主应力梯度路径P0Pn

3 模拟件设计优化方法

3.1 模拟件结构设计

根据模拟件设计原则，在进行模拟件设计时，需要保证零部件考核部位的最大主应力与其附近的最大应力梯度保持一致。针对航空发动机榫头/榫槽特征，初步设计包含双边V形缺口的平板模拟件，如图3所示。对该模拟件施加轴向载荷时，缺口处的应力分布可以模拟榫头/榫槽服役时的应力状态。通过控制双边V形缺口的几何参数（A、B、R）调节缺口根部应力梯度分布，从而实现航空发动机榫头/榫槽的模拟件设计。

图3 模拟件结构

3.2 模拟件优化数学模型建立

上述模拟件需要通过控制双边V形缺口的几何参数（A、B、R）最终获得所需要的缺口根部应力梯度分布，此时需要通过对榫头/榫槽部位的物理模型进行抽象分析，进而建立特征模拟件数学优化模型，该模型主要包括航空发动机榫槽部位优化数学模型的建立、设计变量的确定、目标函数的选取及约束条件的设置等工作[10]。

航空发动机榫头/榫槽特征模拟件形状优化设计可采用的数学模型[11]为

x为优化设计变量，该变量是由n个变量组成的n维向量x=（x1…xn）；f,g,h是与变量x1…xn相关的函数，f(x)是优化目标函数；hi(x)为等式约束条件，i=1，…，m；gj(x)为不等式约束条件，j=1，…，r；S为设计变量的搜索域，是1个n维空间。

利用文献[5]的方法确定最大应力梯度路径，零部件危险部位路径P0Pn上第1主应力分布如图4所示。在开展模拟件优化设计时，将零部件危险部位处最大第1主应力梯度路径P0Pn上各点应力与模拟试件P0Pn上对应各点应力1范数‖ΔS11‖1=‖S11s-S11g‖进行对比。优化目标定义为：特征模拟件第1主应力最大梯度路径上的对应各点应力1范数‖ΔS11‖1=‖S11s-S11g‖达到最小。

图4 零部件危险部位路径P0Pn上第1主应力分布

针对如图3所示的双边V形缺口模拟件，将Python语言与Abaqus有限元分析相结合，进行榫头/榫槽模拟件结构的详细设计。设计变量范围为：A=[20.0，…，30.0]；B=[15.0，…，28.0]；R=[1.0，...，3.0]，通过调整设计变量（A、B、R），优化使得模拟件缺口处沿拉伸方向应力和零部件危险部位第1主应力梯度路径P0Pn上对应点应力的差值最小。模拟件设计优化流程如图5所示。

图5 模拟件设计优化流程

3.3 基于遗传算法的模拟件优化设计

优化设计需要遵循一些运算规则，以获得区域内的最优解。遗传算法[12-13]是一种常用的优化算法，模拟了生物界自然选择和遗传机制，将物种变异和自然选择的过程用于优化选择。遗传算法规定自然界中的每个物种由种群来体现，种群在每一代进化过程中都可能发生基因重组、突变以及引入外来种群，种群中只有适合生存的个体存活，不适应的将被淘汰，最终形成最大适应度的个体[14]。根据预定义的准则函数，需要预先定义处理问题求解的种群运算法则，改进种群法则，规定迭代次数等，最终获得最优解[15]。遗传算法流程如图6所示。

图6 遗传算法流程

遗传算法的优化过程如下：

（1）第i=0代种群随机初始化：G（0）=｛X（1），X（2），…，X（N）｝（其中N为群体个数；i为群体对应的代）。

（2）计算G（i）中所有个体的适应度，利用选择算子生成父代群体Pr。

（3）选择主要是使群体中适应性好的个体的下一代有较高的存活概率。利用给定的概率对父代群体进行交叉变异生成子代群体P。

（4）将i增加1，判断是否满足准则函数。若满足则算法终止；若不满足，则从第（2）步继续迭代运算，直至满足准则函数。

遗传算法基于群体搜索策略和群体中个体间的信息交换，搜索不依赖于梯度信息[16]。因此，遗传算法简单通用，尤其适用于解决传统搜索方法难以处理的复杂非线性问题，便于开展模拟件全局寻优设计工作[17]。该方法不需要设计者对系统有太多了解就可以开展迭代优化选择，变异的存在使得遗传算法可以避免陷入局部最优解，从而获得全局最优解。由于遗传算法计算量庞大，循环迭代，当设定初始种群不合适或者突变概率设定较小时，会出现过早地收敛于局部最优解的情况，从而未得到全局最优解。

4 模拟件设计

4.1 模拟件外观设计

采用双边V形缺口进行榫头/榫槽模拟件设计，并考虑试验件的夹具和载荷量程等，模拟件外观尺寸如图7所示。从图中可见，模拟件试样长、宽、厚分别为170、50、1mm。

图7 模拟件外观尺寸

4.2 模拟件优化结果分析

根据榫头/榫槽应力计算结果可知，危险点位于靠近榫槽槽底部位，该部位存在明显的应力集中。危险点附近的环形路径如图8所示。采用第3.1节中的方法求得通过最危险点处的最大主应力方向（图8中箭头方向），采用第3.2节中第1主应力梯度路径及应力分布的获取方法，结合Abaqus软件的Path命令，以最危险点为中心，以Δr=0.1 mm、2Δr=0.2 mm…8Δr=0.8 mm为半径步长作一系列圆弧，找出每个圆弧上最小第1主应力点，可获得榫槽危险部位路径P0Pn上第1主应力分布，如图9所示。

图8 危险点附近的环形路径

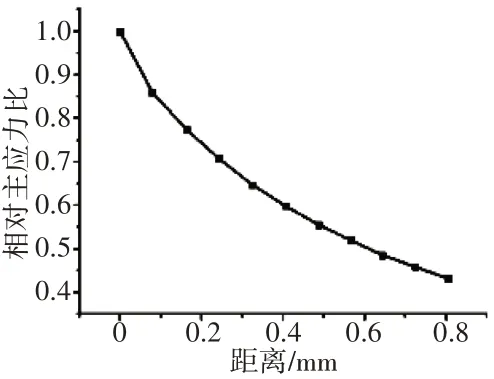
图9 榫槽危险部位路径P0Pn上第1主应力分布

按照第3.2节中的优化流程，以图9给定的榫槽危险部位路径P0Pn上第1主应力分布曲线为目标进行模拟件优化分析，得到优化结果（如图10所示），其中A=31.2、R=1.3、B=10.8，用优化分析得到的几何模型进行应力计算（端部施加100 MPa拉应力），其结果优化目标对比如图11所示，横坐标为主应力方向上距离最危险点的长度（此处取工程裂纹近似长度为0.8 mm）。从图中可见，模拟件与零部件槽底的危险部位第1主应力梯度路径上应力分布吻合得很好。