小格点中的大智慧——对一道课本习题的拓展探究

范明明 郑 金

(广东省佛山市南海外国语学校,528200)

对于教材中的习题,如果仅仅是就题论题,必然会使学生感觉太简单,没有做到由浅入深,更不足以激发学生学习的积极性[1].近日,笔者在处理北师大版课标教材八年级上册第43页第4题时,有意识地引导学生进行由浅入深的拓展探究,最大化地发挥和利用了该习题的教学价值.

一、原题呈现

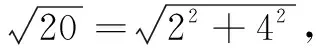
二、拓展探究

1.方法巩固,夯实基础

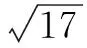
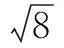
评注虽然大多数同学都能快速解答原题,但仍然有少数同学不能独立完成.为了使班上所有同学都能熟练掌握利用“勾股定理”构造一条长度为无理数的线段的方法,笔者设计了问题1.通过原题的练习和问题1的巩固,同学们基本都能深刻理解并熟练掌握此种构图方法.

2.问题升级,提升难度

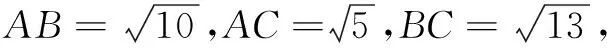
评注相对于问题1来说,问题2中的三条线段在位置上不再是相互独立的而是有了一定的关联性,即要首尾相连组成三角形,这也是该问题的难点所在.在教学时,笔者通过逐步引导,形象直观地突破了这一难点,求三角形的面积自然变得水到渠成.上述探究过程,不仅培养了学生的运算能力、直观想象、逻辑思维,更渗透了建模思想和数形结合思想,为后面问题的研究作了铺垫作用.

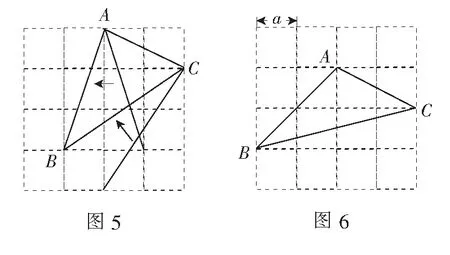
3.深度探究,提升思维

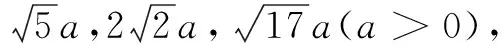
评注问题3将问题2中确定的边长变为不确定的边长,旨在引导学生将特殊问题转化为一般问题,除了进一步渗透数形结合思想和建模思想外,还重点体现了由特殊到一般的数学思想.当然,运算能力、直观想象、逻辑思维也得到了更进一步的发展.

4.变式拓展,提高能力

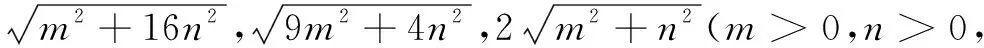
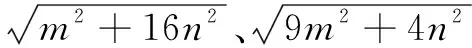
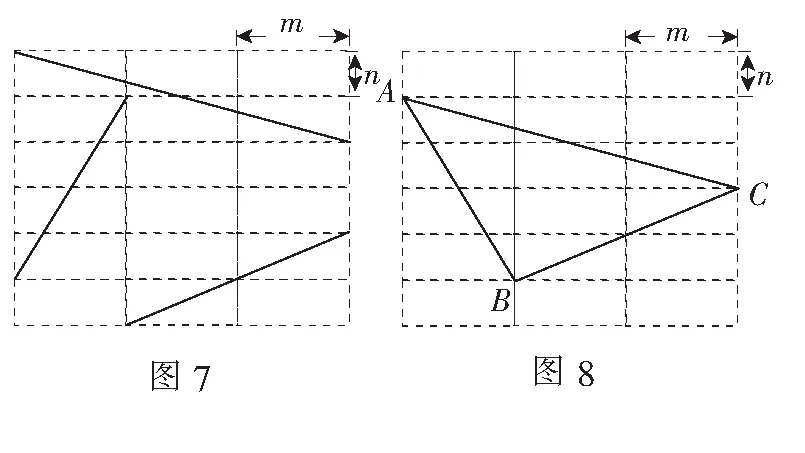
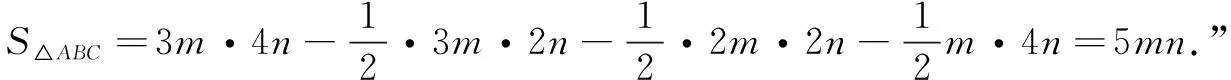
评注问题4是对问题3的进一步拓展,旨在引导学生理解求此类问题的本质,促进数学素养培育的真实落地.问题4虽然变得更复杂,但万变不离其宗,变的是在构图时需要将正方形方格变为长方形网格,不变的是数形结合思想以及建模思想的运用.

三、感悟与思考

1.立足教材资源,适度拓展探究

叶圣陶先生说过:“教材无非就是个例子.教材只能作为教学的依据,要教得好,使学生受益,还要靠教师善于运用.”[2]《义务教育数学课程标准(2011年版)》中也特别强调,教师在教学活动中要创造性地使用教材,在教材内容所要求的知识和方法的基础上,结合学生的实际情况,进行适当的变式或拓展,以满足不同层次学生的需要.

正方形网格中的作图,作为尺规作图的补充和拓展,对学生的直观想象能力、逻辑推理能力、运算能力以及创新能力的培养都有着积极的作用,在近年来越来越受到人们的重视.笔者以教材中的一道网格作图题为出发点,在引导学生掌握利用勾股定理进行构图的基础上,继续帮助学生巩固方法、夯实基础,再用所学的知识与方法进行拓展研究.这不仅激发了学生的学习兴趣,也促进了学生数学能力及核心素养的提升.

2.渗透数学思想,提升思维能力

知识是载体,方法是手段,思想是核心,提高数学核心素养的关键在于要帮助学生在掌握知识的基础上形成对数学思想方法的认识、理解和运用.换句话说,“数学思想方法蕴含在数学知识形成、发展和应用的过程中,是数学知识和方法在更高层次上的抽象和概括”[3].因此,教师在平时的教学活动中不能只关注对具体知识的传授,更要注重对数学思想方法的渗透,真正达到提升学生的数学能力和落实培育学生的数学核心素养这一最终目的.

笔者引导学生从画一条线段出发,到构造一个三边长都确定的三角形并求面积,再到求一个三边长都不确定的三角形的面积,层层递进、逐步深入.学生在画图过程中,需要经历从有网格到无网格、从正方形网格到长方形网格的变换过程.可以说,笔者以根据“勾股定理”画一条长度为无理数的线段为知识和方法的载体,引导学生总结利用网格求三角形面积问题的一般方法,更将建模思想、数形结合思想以及从特殊到一般的数学思想渗透其中,让学生在理解知识、掌握方法的基础上更体会了数学思想的重要价值,有效地促进了学生的数学思维能力的提升.