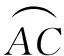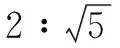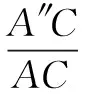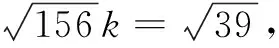“连杆变换”模型及其应用

苑建广

(河北省晋州市教育局教研室,052260)

一、“连杆变换”模型

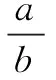
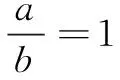
当θ=0°时,连杆变换退化为位似变换.

“连杆变换”模型有时被称作“瓜豆原理”,取“种瓜得瓜,种豆得豆”之意,它常常以隐蔽的方式藏在题目背景中,作为压轴题的常用命题素材.

二、“连杆变换”模型的应用

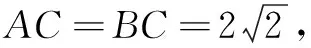
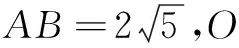
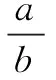
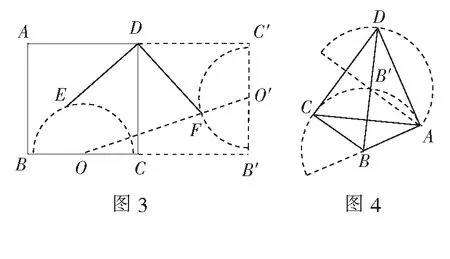
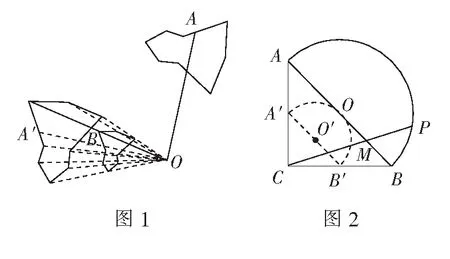
例3(2022年宝鸡模拟题)如图4,四边形ABCD中(B,D在AC的异侧),AB=BC=3,AC=AD,∠ACD=60°,则对角线BD的长不可能是( )

(A)5.3 (B)5.5 (C)6 (D)6.5

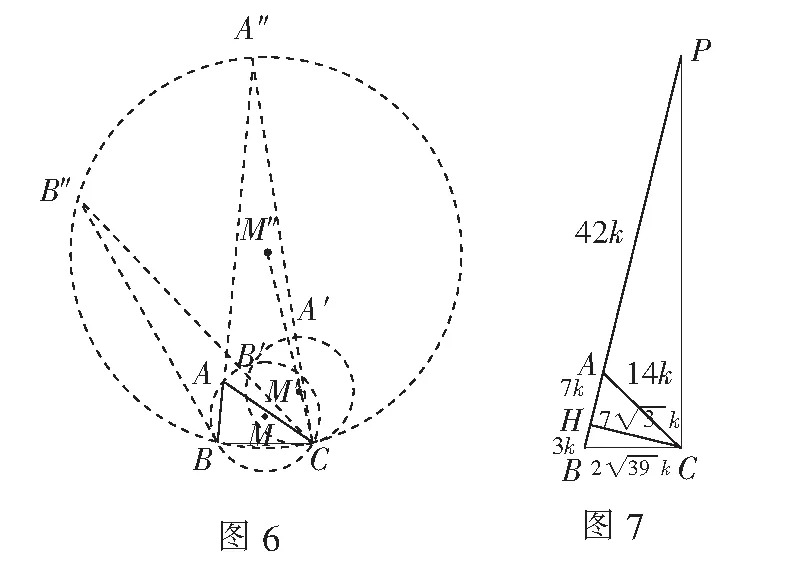
显然,BD的最小值大于AB=3,而BD取最大值时,BD经过圆心B′.又∆BAB′是正三角形,可知∆BAD是直角三角形,所以BD=2AB=6,即3

(A)一直变小,且最大值为5

(B)一直变小,且最小值为0

(C)先变大再变小,且最小值为0

(D)先变大再变小,且最大值为5

分析从构造“c+3b”出发,考虑延长BA至点A″,使AA″=3b,则BA″=c+3b.

显然,∆A″AC的形状固定:∠A″AC=120°,AC=b,AA″=3b.

易知∆B″BC∽∆A″AC,则∠B″BC=∠A″AC=120°,所以点B在圆M″上.

显然有,当BA″为直径时,c+3b最大.

《义务教育数学课程标准(2022年版)》明确指出:“模型观念主要是指对运用数学模型解决实际问题的清晰的认识,知道数学模型……，感悟数学模型应用的普遍性.”本文正是基于这一考虑,对“连杆变换”模型的特征及应用上的技巧做了一些梳理.上述几个问题的突破,是在探索的过程中发现其中隐藏了“连杆变换”模型,从而顺利打开思路.