一类圆内接四边形的系列结论及应用——以一道中考模拟题为例

虞 会

(浙江省宁波市镇海蛟川书院,315201)

一、试题呈现

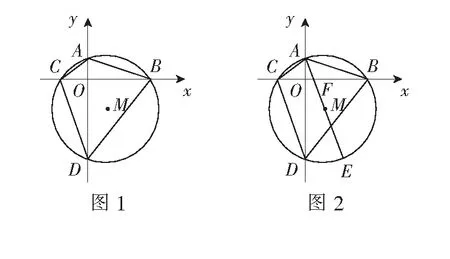
(1)∠DAB=______(请用α的代数式表示),并求证:DA=DB;

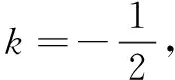
(3) 如图2,连结AM并延长,交BC于点F, 交⊙M于点E,

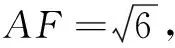
② 若3BF=2OD,请直接写出四边形ABDC的面积.

此题为2022年宁波市镇海区中考模拟卷中的一道压轴题,涉及圆的基本性质、直角三角形、勾股定理、相似三角形等相关知识,三小问难度层层递进,全面考查了学生分析问题,解决问题的能力.从学生的答题情况来看,第(1)、(2)问学生尚能解决,第(3)问很多学生难以入手,究其原因还是对特殊圆内接四边形的认识不足.

二、图形分析

笔者发现,在去掉平面直角坐标系的背景后,此题可归结为圆中的一类内接四边形(两条对角线互相垂直且一条对角线等于一条边的圆内接四边形)问题.

1.图形初步认识

如图3,已知在⊙O的内接四边形ABCD中,AB=AC,AC⊥BD,从此图中可以得出哪些结论?

从角的方面考虑:

结论1:若∠CAD=α,则图形中所有的角都可以用α来表示.

特别地,∠BAC=∠BDC=2α.

从线段的方面考虑:

结论2:因为AC⊥BD,所以有四组线段满足勾股定理.

结论3:由于四边形ABCD内接于⊙O,故有两对相似三角形.

结论4:(托勒密定理)AB·CD+AD·BC=AC·BD.

从角和线段相结合的方面考虑:

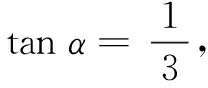
2.图形变式认识

变式1如图4,已知在⊙O的内接四边形ABCD中,AB=AC,AC⊥BD,连结AO交BD于点F,连结CF,从此图中又能得出哪些关键结论?

结论6:∆ABF≌∆ACF≌∆ADC,

结论7:CD+DE=BE.

由结论6,可得BF=CF=CD,FE=DE,从而可证结论7.

结论7 其实就是阿基米德折弦定理,如果知道此定理,则在图形初步认识里面就可以得出结论7.

结论8:∆AFD∽∆ABC(手拉手相似),Rt∆AEF∽Rt∆BEC,Rt∆ABE∽Rt∆FCE.

变式2如图5,已知在⊙O的内接四边形ABCD中,AB=AC,AC⊥BD,连结BO交AC于点G,从此图中又能得出哪些关键结论?

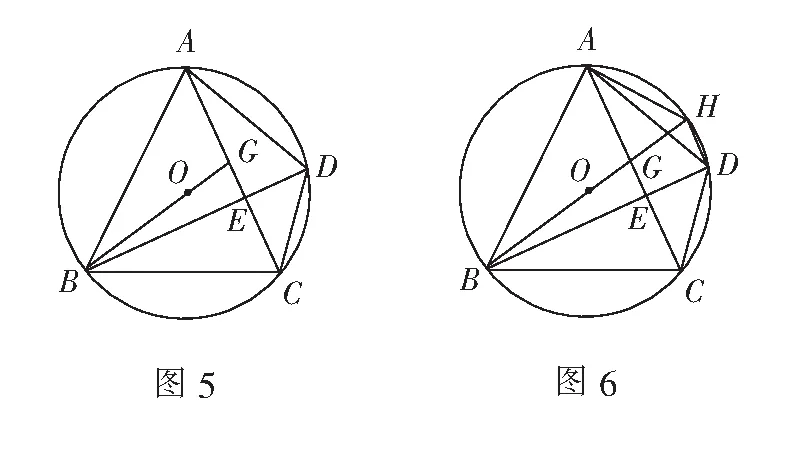
结论9:∆ABG∽∆DBC和∆ABD∽∆GBC(手拉手相似).

结论10:若已知AG,CG的长,则可求得图中所有线段的长.

结论11:如图6,若延长BG交⊙O于点H,连结AH,DH,则四边形AHDC为等腰梯形.

变式3如图7,已知在⊙O的内接四边形ABCD中,AB=AC,AC⊥BD,连结CO交BD于点H,延长CO交AB于点Q,从此图中又能得出哪些关键结论?

结论12:CQ∥AD.

结论13:DC=DH.

结论14:BH=2DE.

∵BE=DE+DC(结论7),

DC=DH(结论13),

∴BH=BE-HE

=DE+DH-HE=2DE.

结论15:∆ECH∽∆EBC.

三、试题解答

(1) 由圆的性质,可得∠DAB=∠DCB=90°-α.

∵∠DBC=∠CAD=90°-2α,

∠ABC=∠ADC=α,

∴∠DBA=90°-α.

∴∠DAB=∠DBA,进而得DA=DB.

在Rt∆AOC中,由结论5,可得

OC∶OA∶AC=3∶4∶5.

由结论15,可得∆OAF∽∆OBA,

解得OB=5,∴BF=4.

② 由结论14,可知BF=2CO.

∴3×2CO=2OD,即3CO=OD,

在Rt∆AOC中,由结论5,可得

AO∶CO∶AC=3∶4∶5.

四、解后思考

正如章建跃博士在《几何研究中的数学思维方式》中所说:几何学的课题就是研究和理解几何图形的本质与结构.本质是指事物的根本性质,是事物自身组成要素之间相对稳定的内在联系;结构是指事物内部各组成要素之间的相互联系、相互作用的方式.在近几年的中考模拟或者中考试题中,对压轴题的要求往往是去模型化,更加关注学生的思维,更趋向于考查学生的分析问题,解决问题的能力.所以,教师在平时讲解几何综合题时,一定要追本溯源,让学生学会拆分复杂的图形,厘清基本图形之间的相互联系,能迁移所掌握的基本图形性质,这样才能提高学生应用知识,解决问题的能力.