“歪打正着”话“存在”

朱明明

(江苏省如东高级中学,226400)

存在性问题涉及的数学知识点多、综合性强,在中学数学中有重要的地位.解决这类问题时常由于对“存在性”的理解发生偏差,导致转化不“等价”,从而引发错误,特别是在“歪打正着”得到正确结果的情形下,错误隐蔽更深且不易觉察,需要引起重视.

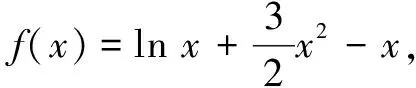
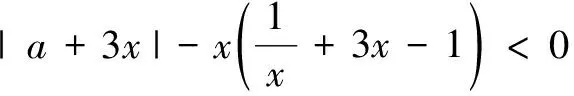
-3x2-2x-1

①

亦即

(-3x2-2x-1)min

②

令g(x)=-3x2-2x-1,x∈[1,2],易得g(x)min=-17.令h(x)=3x2-4x+1,x∈[1,2],易得h(x)max=5.故a∈(-17,5).

剖析本解答结果正确,过程上似乎也没什么问题.事实果真如此吗?

我们知道,命题“∃x∈[m,n],使a>g(x)”等价于命题“a>g(x)min,x∈[m,n]”,命题“∃x∈[m,n],使a

但是,命题“∃x∈[m,n],使g(x)

那么,上述解答给出的结果为什么恰好是正确的呢?

在同一坐标系中画出g(x)与h(x)的图象,可以发现在区间[1,2]上g(x)为减函数,h(x)为增函数,从而g(x)min与h(x)max在x=2时同时取得!由此可知上述解答中从① 式推出② 式并不具备一般性意义,有点“歪打正着”的感觉!

无独有偶,请看下一道题.

探究本题是某地高考模拟题.刘卫东老师在文[1]中结合对原参考答案的剖析,通过分类的方法给出了从正面思考的解题过程,并指出:一般地,对∀x∈D(区间),“命题p∨q恒成立”并不等价于“命题p恒成立或命题q恒成立”,而且要解决p∨q型恒成立问题比较困难.因此,刘老师建议解题时最好避免将问题转化为这种形式.笔者思考的是,如果解题时转化成了该形式,有没有一种方法可以做下去呢?经过探索,笔者发现借助否命题从反面来考虑,即利用命题“∀x∈D,p∨q恒成立”的否定“∃x∈D,p且q”来实施解答.

综上,注意到U={c|0