一道高考解析几何题的思考与探索

常梨君 金一鸣

(江苏省常州市田家炳高级中学,213000)

解析几何在高中数学学习中占有举足轻重的地位,近几年高考对直线与圆锥曲线相交问题的考查更是主流.这类问题的常见解题思路为:将条件和结论坐标化,联立直线与圆锥曲线方程,利用韦达定理解决问题.解析几何问题的解题思路是清晰的,但多元变量运算的繁、难是导致学生“畏算”的主要因素.若解题方法选取得当,则会将大大降低运算难度,实现“巧算”.本文以2022年新高考I卷第21题第(1)问为载体,探讨解析几何问题解决的常见解题策略(此题的背景和方法也可推广到椭圆和抛物线).

一、试题呈现

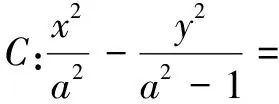
(1)求l的斜率;

二、解法赏析

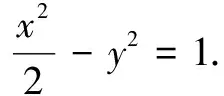
1.常见解法

解法1(设而不求)

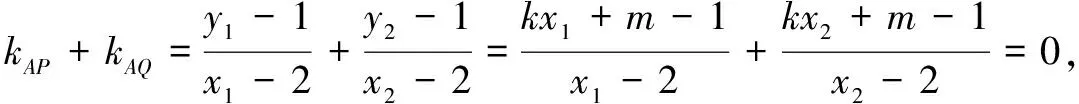
2kx1x2+(m-2k-1)(x1+x2)-4(m-1)=0.

①

当m=1-2k时,直线PQ的方程为y=kx+1-2k,过定点A(2,1),不合题意,舍去.所以k=-1.

评注从结论出发,设出目标直线PQ的方程(含双参k,m),借助条件kAP+kAQ=0构建k和m的方程,找出k和m的等量关系,得到定值,这是通性通法,易想但运算量不小.

解法2(设而求之)

设直线AP，AQ的斜率分别为k1,k2,点P(x1,y1),Q(x2,y2).

由k1+k2=0,得直线PQ的斜率

评注由kAP+kAQ=0联想到设出直线AP,AQ方程,联立双曲线方程求出点P,Q的坐标,再由直线斜率的定义直接求定值,也是常见方法.但此法适用的前提是直线与双曲线的两个交点之一已知,利用韦达定理的积式可求另一交点,运算量同样大.

由同一点出发的双曲线的两条割线(形似),应当具有类似的性质,如直线的方程、交点的坐标等相似性.以此为基础,可从函数与方程的角度出发,构造同构方程解决问题.

解法3(利用点P,Q在同一直线上构造同构式)

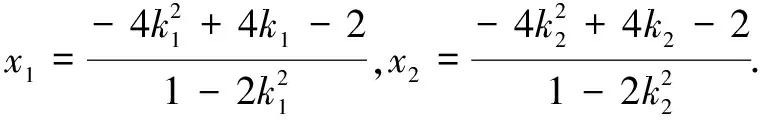
由题意知直线PQ的斜率存在,可设其方程为y=kx+m,将点P,Q的坐标代入并整理,得

其中的p=2+4k+2m,q=4+4k,r=2k-m+1.

解法4(利用点P,Q是三条曲线的公共点构造同构式)

由题意可设直线PQ,AP,AQ的方程分别为y=kx+m,y-1=k1(x-2)，y-1=k2(x-2).

能够称之为旅游资源的生态环境一定是美的、舒适的、自然的，能够带给旅游者一定的身心慰藉，带来舒适的体验和情绪的是放，这样的生态环境能够成为旅游资源开发的重点。因此，要实现地区旅游资源的开发和利用，首先应该要保护好、整治好地区的生态环境，不断提升旅游资源的质量和水平，才能将地区打造成优质的旅游地带。

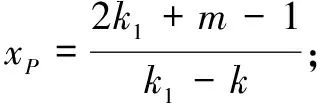
②

其中的p=2+4k+2m,q=4+4k,r=2k-m+1.

同理可得

③

由② ③ 两式可知k1,k2为方程px2-qx+r=0的两个不等实根,下同解法3,不难得到k=-1.

评注将形的相似性用相同结构的两个方程刻画,多变量方程中提取主元抽象出同构方程,是同构法解题的基本思路.但由k1+k2=0联想到构造关于k的二次方程,整体处理,这个视角的转变才是难点,是有数学高级思维参与的数学运算,体现了设而不求的解题思想,相应运算量适中.

3.新思路2——齐次化方程法

解法5由直线PQ不过点A,设其方程为m(x-2)+n(y-1)=1.

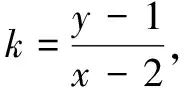
(4n+2)k2+(4m-4n)k-4m-1=0.

④

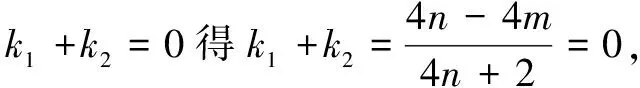
评注以公共点A(2,1)为基础,构造出类似结构的割线方程和双曲线方程;再由k1+k2=0出发,利用“1”的代换,直接构造出关于k的二次方程,可谓神来之笔.究其本质,乃是坐标系平移变换,即将点A(2,1)平移为坐标原点.

4.新思路3——点差法

点差法在解决中点弦问题时有很好的优势,但在数学教学中不能将这种印象固化为一种技巧.“点差”的本质是利用二次方程的加减整体消元,得到斜率与两个点坐标和的关系式.根据这个思路,可得解法6.

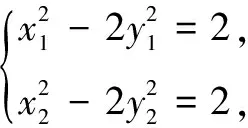
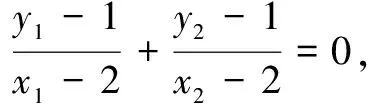
x1y2+x2y1-(x1+x2)-2(y1+y2)+4=0,

⑤

x1y2+x2y1+(x1+x2)+2(y1+y2)+4=0.

⑥

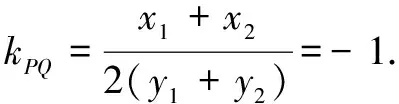
三、结束语

《新课标》明确指出:数学运算是在明晰运算对象的基础上,依据运算解决数学问题的素养,要求学生理解运算对象,探究运算方向,选择运算方法,设计运算程序,求得运算结果[1].学生基于运算对象选择的路径不同,导致的运算长度和繁简程度也不同.上述六种解法体现了不同数学思想指导下的不同运算策略的选择,“设而不求”和“设而求之”是解析几何中常用的数学思想,选择解法1和解法2表明学生“能够在熟悉的情境中了解运算对象,提出运算问题”,属于数学运算核心素养水平一.后续四种解法引入了“同构”、“齐次化”、“点差”思想,实现了不同程度上的运算简化,这要求学生要有在综合情境中创造性地转化运算问题的能力,属于数学运算核心素养水平三.由此可见,高水平的数学运算一定有逻辑推理的参与.

将解析几何问题从“联立求解”转移到“识图析图”,从繁琐的数式运算转向分析推理型运算,让学生体会更多“设而不求”、“整体运算”的计算精髓.只有这样，才能真正提升运算素养,培养学生不怕算的毅力,以适应新高考对学生数学核心素养的要求!

(后续)