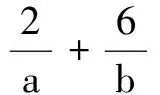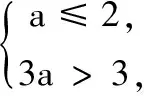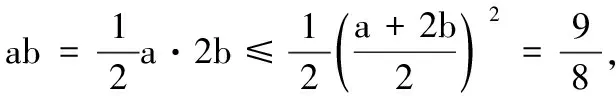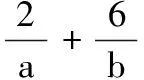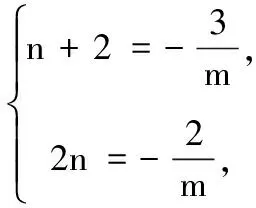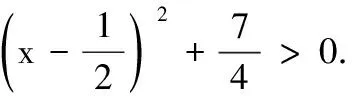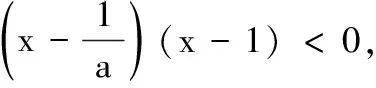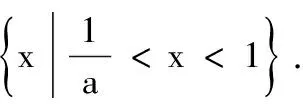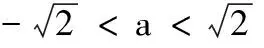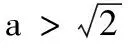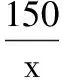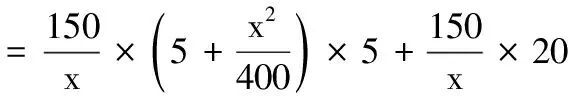高一数学测试
2022-11-28
一、单项选择题(本大题共8小题,每小题5分,计40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.已知全集U={0,1,2,3,4},集合A={1,2,3},B={2,4},则(UA)∩B=( )
(A){4} (B){2,4}
(C){0,4} (D){2}
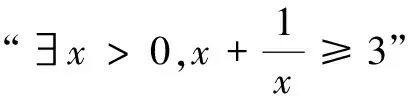
3.设x∈R,则“0 (A)充分而不必要条件 (B)必要而不充分条件 (C)充要条件 (D)既不充分也不必要条件 4.已知a,b,c,为实数,且a>b>0,则下列不等式不一定正确的是( ) 5.已知集合M={x|x2-3x-28≤0},N={x|x2-x-6>0},则M∩N为( ) (A){x|-4≤x<-2或3 (B){x|-4 (C){x|x≤-2或x>3} (D){x|x<-2或x≥3} 6.已知p:|x+a|<2,q:x≥a,且p是q的充分不必要条件,则实数a的取值范围是( ) (A)a≤-1 (B)a<-1 (C)a≥1 (D)a>1 7.要制作一个容积为4 m3,高为1 m的无盖长方体容器.已知该容器的底面造价是每平方米20元,侧面造价是每平方米10元,则该容器的最低总造价是( ) (A)80元 (B)120元 (C)160元 (D)240元 8.下列命题中是真命题的是( ) (A)已知a,b∈R,则“a2>b2”是“|a|>|b|”的充分不必要条件( ) (B)|x|2+|x|-2=0有四个实数根 (C)若x2-3x+2≠0,则x≠2或x≠1 9.已知集合A={1,2,3},则下列表示方法正确的是( ) (A)∅⊆A(B){1,2}∈A (C)A⊆N*(D)1⊆A 10.已知集合A={x|x2-2x-3=0},B={x|ax=1},若B⊆A,则实数a的可能取值( ) 11.下列命题中正确的是( ) 12.下列说法中正确的为( ) (A)集合A={x|ax2+2x+a=0,a∈R},若集合A有且仅有2个子集,则a的值为±1 (B)若一元二次不等式kx2-6kx+k+8≥0解集为R,则k的取值范围为0 (C)设集合M={1,2},N={a2},则“a=1”是“N⊆M”的充分不必要条件 13.已知命题:p:∃x∈R,使x2+2x=3,则p是______. 14.某公司租地建仓库,每月土地费用与仓库到车站距离成反比,而每月货物的运输费用与仓库到车站距离成正比.如果在距离车站10 km处建仓库,则土地费用和运输费用分别为2万元和8万元,那么要使两项费用之和最小,仓库应建在离车站______km处. 15.已知1≤a-b≤2,2≤a+b≤4,则4a-2b取值范围是______. 16.设A,B是非空集合,定义A⊗B={x|x∈(A∪B)且x∉(A∩B)}.若集合A={x|0 17.(本小题满分10分)设集合A={x|(x-3)(x-a)=0,a∈R},B={x|(x-4)(x-1)=0}. (1)若a=1时,求A∩B,A∪B; (2)设C=A∪B,若集合C的子集有8个,求实数a的取值集合. 18.(本小题满分12分)设命题p:实数x满足(x-a)(x-3a)<0(其中a>0),命题q:实数x满足2 (1)若a=1,p和q都为真,求实数x的取值范围; (2)若q是p的充分不必要条件,求实数a的取值范围. 19.(本小题满分12分)设a>0,b>0,且a+2b=3. (1)求ab的最大值; 20.(本小题满分12分)已知不等式mx2+3x-2>0的解集为{x|n (1)求m,n的值,并求不等式nx2+mx+2>0的解集; (2)解关于x的不等式ax2-(n+a)x-m>0(a∈R,且a≤0). 21.(本小题满分10分)解关于x的不等式x2-2ax+2≤0. (1)求这次行车总费用y(单位:元)关于x的表达式; (2)当x为何值时,这次行车的总费用最低?求出最低费用的值. 参考答案 一、单项选择题 1.A; 2.C; 3.B; 4.B; 5.A; 6.A; 7.C; 8.D. 二、多项选择题 9.AC;10.ACD;11.ABC;12.BCD. 三、填空题 13.∀x∈R,x2+2x≠3;14.5; 15.5≤4a-2b≤10; 16.{0}∪[2,+∞). 四、解答题 17.(1)当a=1时,依题意得A={1,3},B={1,4}. 所以A∩B={1},A∪B={1,3,4}. (2)因为C=A∪B,集合C的子集有8个,所以集合C中有3个元素,而1,3,4∈C,故实数a的取值集合为{1,3,4}. 18.(1)由(x-a)(x-3a)<0,且a>0,得a 又命题q:2 (2)设A={x|a 因为q是p充分不必要条件,所以BA. (2)由(1)知ax2-(n+a)x-m>0可化为ax2-(1+a)x+1>0,即(ax-1)(x-1)>0. 当a=0时,-x+1>0,解得x<1. (2)由基本不等式,可得 =225,
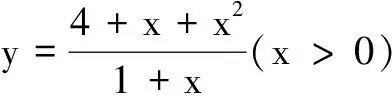
二、多项选择题(本大题共4小题,每小题5分,计20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分)
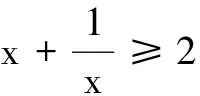
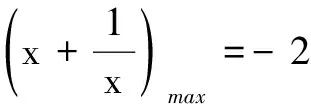

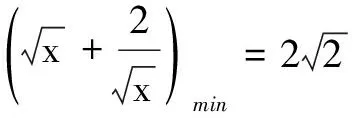
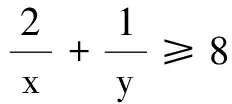
三、填空题(本大题共4小题,每小题5分,计20分)
四、解答题(本大题共6小题,计70分.解答应写出文字说明、证明过程或演算步骤)