构造三角形模型求解代数题

陈 翔

(江苏省泗阳中学，264200)

正弦定理、余弦定理是联系三角形的边与角关系的两个重要定理,在解题中有着广泛的应用.对于结构特征与正、余弦定理公式相类似的代数式子,我们可以通过构造三角形模型,运用正、余弦定理求解.这种方法简捷明快、颇具新意.下面举例说明.

一、求代数式的值

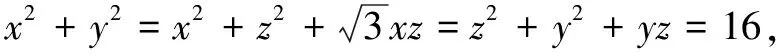
解由已知条件中的连等式,联想到解三角形中的余弦定理,构造边长为4的等边三角形∆ABC,P是∆ABC内定点，连结PA，PB，PC，设PA=x,PB=y,PC=z.

在∆PAB中，由条件x2+y2=42,可得∠APB=90°.

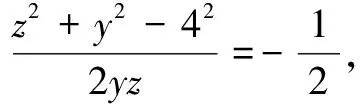
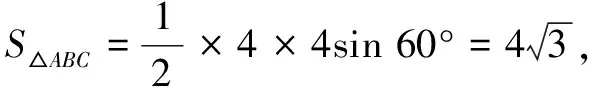
评注本题依据已知条件中连等式的特点,通过构造三角形,然后进行分割,运用余弦定理和三角形面积公式,整体求得结论,十分巧妙.

二、求代数式的最值

例2设实数x,y满足x2-xy+y2=1,求x2-y2的最大值与最小值.

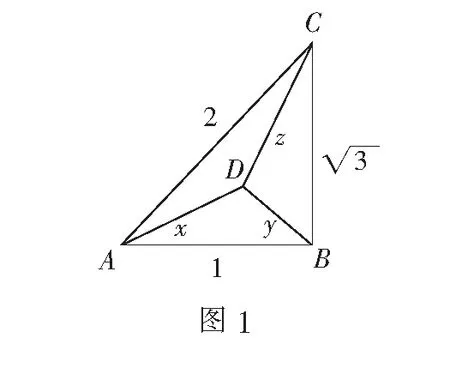
解观察已知条件的结构,发现和余弦定理的结构相似,故构造∆ABC,使∠ACB=60°,AB=1,BC=x,AC=y.

在∆ABC中,由余弦定理,可知x,y满足x2-xy+y2=1.

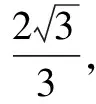
评注本解法利用正弦定理,把x,y用三角函数表示出来,再通过三角变化把所求式化为三角函数的形式,从而求出最值.

三、解方程(组)

例3设正实数x,y,z满足

求x+y+z的值.

分析观察方程组中每一个方程的结构,发现与余弦定理的结构相似,考虑构造三角形求解.

解原方程组可化为

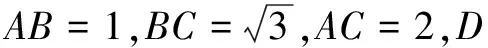
由此将原方程组中三式相加,并将xy+yz+zx=2代入,可得x2+y2+z2=3.于是

x+y+z

评注这是代数问题用几何方法求解的范例.根据已知条件构建几何图形,进而用已知几何图形的性质求得代数问题的解.

四、证明不等式

例4(2022年全国中学生数学奥林匹克竞赛广西赛区预赛题)已知x,y,z都是正数,且(x+y-z)(y+z-x)(z+x-y)>0,求证：x(y+z)2+y(z+x)2+z(x+y)2-(x3+y3+z3)≤9xyz.

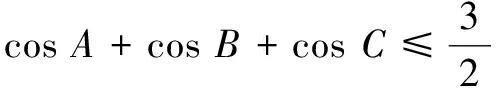
构造法是一种重要的数学思维方法,它是创造力的较高表现形式,是高考考查的热点.在数学解题中应注意依据题目特征,类比相关知识,通过构造数学模型来促使问题的解决,从而培养思维的创造性.构造时,需跳出题外,高屋建瓴,方可遂愿.