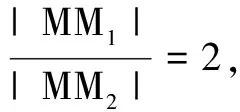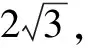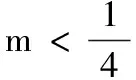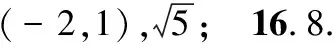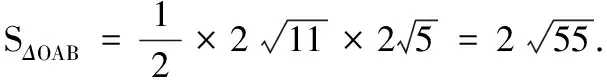高二数学测试
2022-11-28
一、单项选择题(本大题共8小题,每小题5分,计40分)
1.两条平行直线3x-4y-2=0与3x-4y+3=0之间的距离是( )
(A)1 (B)2 (C)3 (D)4
2.若点(1,1)在圆(x-a)2+y2=5的外部,则实数a的取值范围是( )
(A)(-1,3)
(B)(-2,2)
(C)(-∞,-1)∪(3,+∞)
(D)(-∞,-2)∪(2,+∞)
3.如图,已知直线l1,l2,l3的斜率分别为k1,k2,k3,则( )
(A)k1 (C)k3 4.已知直线l1:x-y+1=0,l2:x-2=0,则过l1和l2的交点且与直线3x+4y-5=0垂直的直线方程为( ) (A)3x-4y-1=0 (B)3x-4y+1=0 (C)4x-3y-1=0 (D)4x-3y+1=0 5.方程y=k(x-2)表示( ) (A)通过点(2,0)的所有直线 (B)通过点(2,0)且不垂直于y轴的所有直线 (C)通过点(2,0)且不垂直于x轴的所有直线 (D)通过点(2,0)且除去x轴的所有直线 6.已知圆C1:(x-3)2+(y+2)2=1与圆C2:(x-7)2+(y-1)2=50-a,若圆C1与圆C2有且仅有一个公共点,则实数a等于( ) (A)14 (B)34 (C)14或45 (D)34或14 7.若圆x2+y2=1上总存在两个点到点(a,1)的距离为2,则实数a的取值范围是( ) (C)(-1,0)∪(0,1) (D)(-1,1) 9.已知等边三角形ABC的两个顶点A(0,0),B(4,0),则BC边所在直线的方程可能是( ) 10.已知点P(1,1)与直线l:x-y+1=0,下列说法正确的是( ) (A)过点P且截距相等的直线与直线l一定垂直 (B)过点P且与坐标轴围成三角形的面积为2的直线有4条 (C)点P关于直线l的对称点坐标为(0,2) (D)直线l关于点P对称的直线方程为x-y-1=0 11.对于圆x2+y2=16,(x-4)2+(y+3)2=r2(r>0),下列说法正确的是( ) (A)若两圆内切,则r=9 (B)若两圆的公共弦所在直线的方程为8x-6y-37=0,则r=2 (C)若两圆在交点处的切线互相垂直,则r=3 (D)若两圆有三条公切线,则r=2 (A)若c=0,则点O在圆C上 (C)若点O在圆C内部,则c的取值范围为(0,+∞) 14.方程x2+y2+4mx-2y+5m=0表示圆,则m的取值范围为______. 15.直线l:x+my-m+2=0(m∈R)过定点______,原点到直线l的距离的最大值为______. 16.已知直线l:y=x-1与x轴的交点为F,A,B是直线l上的两个动点,点P是线段AB上的任意一点,点P到直线x=-1的距离为d.若d≥PF恒成立,则线段AB的最大长度为______. 17.(本小题满分10分)在∆ABC中,已知点A(1,1),B(2,-3),C(3,5),写出满足下列条件的直线方程. (1)BC边上的高线的方程; (2)BC边的垂直平分线的方程. 18.(本小题满分12分)已知圆过点A(1,-2),B(-1,4). (1)求圆心在直线2x-y-4=0上的圆的标准方程; (2)若圆心的纵坐标为2,求相应圆的标准方程. 19.(本小题满分12分)从① 与直线4x-3y+5=0垂直,② 过点(5,-5),③ 与直线3x+4y+2=0平行这三个条件中任选一个,补充在下面的问题中,并加以解答. 问题:已知直线l过点P(1,-2),且______. (1)求直线l的一般式方程; (2)若直线l与圆x2+y2=5相交于点P,Q,求弦PQ的长. (注:如果选择多个条件分别解答,按第一个解答计分) (1)求C的方程; (2)设直线l与C相交于A,B两点,且AB的中点N(6,-2),求S∆OAB(O为坐标原点). 21.(本小题满分12分)过点P(2,1)作直线l分别交x轴、y轴的正半轴于A,B两点. (1)求|OA||OB|的最小值,及此时直线l的截距式方程; (2)求|PA||PB|的最小值,及此时直线l的截距式方程. (1)求圆C的标准方程. (2)设过点M(0,3)的直线l与圆C交于不同的两点A,B,以OA,OB为邻边作平行四边形OADB.是否存在这样的直线l,使得直线OD与MC恰好平行?如果存在,求出l的方程;如果不存在,请说明理由. 参考答案 一、单项选择题 1.A;2.C;3.D;4.D;5.C; 6.D;7.A;8.C. 二、多项选择题 9.BC;10.CD;11.ABC;12.ACD. 三、填空题 四、解答题 又圆心也在直线2x-y-4=0上,所以圆心是这两条直线的交点. (2)设圆心的坐标为(m,2).由圆心所在直线的方程为x-3y+3=0,得m-3×2+3=0,解得m=3. 19.(1)方案1选条件①. 方案2选条件②. 方案3选条件③. (2)方案1选条件①. 方案2选条件②. 解析同方案1中(2). 方案3选条件③. 解析同方案1中(2). 两边平方并整理,可得x2+y2-10x+9=0,所以C的方程为(x-5)2+y2=16. |PA||PB| 又因为圆C的面积S=πr2<13,所以a=1,r=2.于是圆C的标准方程为(x-1)2+y2=4. (2)当直线l的斜率不存在时,其方程为x=0,不满足题意. (1+k2)x2+(6k-2)x+6=0. 设点A(x1,y1),B(x2,y2),则有

二、多项选择题(本大题共4小题,每小题5分,计20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分)
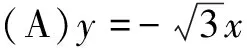
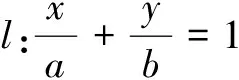
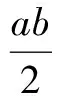
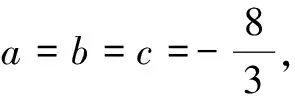
三、填空题(本大题共4小题,每小题5分,计20分)
四、解答题(本大题共6小题,计70分.解答应写出文字说明、证明过程或演算步骤)