深度整合教材 着力德育渗透
——以“事件的相互独立性”教学设计为例
2022-11-28任冬宇
任冬宇
(云南师范大学数学学院,650500)
一、背景
2017年教育部颁布了《中小学德育工作指南》,提出不同学科应承担的德育任务,要求数学、物理、化学等学科,要帮助学生逐步形成敢于创新、求真求实的思想品质[1].教学是德育渗透的主渠道之一,而教学设计作为课堂的预设和文本载体,在其中渗透德育对落实立德树人的根本任务具有实质性意义.
2019年出版的《普通高中教科书·数学(人教A版)》(以下简称“新教材”)不同于《普通高中实验教科书·数学(人教A 版)》(以下简称“旧教材”)模块式编排方式,其中概率章节的编排变动较大,类比函数学习,教材采用一套更系统、集中的研究路径[2].但在教学方面,一项针对全国重点高中数学教师概率教学的调查研究显示,相比几何、代数等内容的教学,教师在进行概率教学时,往往更易陷入困境,即使是身处教学质量金字塔顶部的重点高中,概率教学也往往存在着效果不佳的情况[3].
基于以上分析,笔者选取新教材必修第二册第十章第二节“事件的相互独立性”进行教学设计,以期引起一线教师对德育视域下教学设计更广泛的思考.
二、教学设计要素分析
1.教材分析
在新教材中,该节内容是在学生已学互斥事件和对立事件的基础上,进一步了解事件之间的关系及相应概率的计算.旧教材将本节内容设置在选修2-3,以条件概率的学习为基础.这样的编排顺序不仅冲淡了独立性的概念,而且过于强调独立性和条件概率的联系,忽视了二者之间的区别.新教材将条件概率设置在选择性必修第三册,而将该内容提前到必修第二册.这样的编排顺序较好地说明二者在概率学科中承担的不同使命[4].因此,授课时要改变以往的思维模式.
2.学情分析
在知识方面,通过前几节课的学习,学生已初步掌握了和事件、积事件、互斥事件、对立事件等事件的关系和运算,也掌握了古典概型及概率的基本性质,为学习事件的相互独立性奠定了基础;在能力方面,高一学生已具备一定的试验、观察、分析、发现、归纳等能力,但思维的严谨性相对薄弱,仍需教师引导其由感性认识上升到理性认识,进一步得出事件的相互独立性的公式;在情感方面,学生更愿意接受学中乐,乐中学的教学模式.
3.教学重点与难点
教学重点两个事件相互独立的直观意义及定义,利用事件的独立性解决实际问题.
教学难点在实际问题情境中,判断事件的独立性.
4.教学目标与方法
(1)教学目标
① 结合有限样本空间,理解两事件相互独立的直观意义.在掌握乘法公式P(AB)=P(A)P(B)的基础上,结合古典概型,利用对立事件、互斥事件的概率公式进行计算.
② 通过试验、观察、发现、联想、推理、归纳等环节,经历探索两事件相互独立的过程,促进学生理性思维能力的发展.
③ 通过试验探究启发学生获取新知,培养学生学与乐相结合的数学情感,体验特殊与一般、正难则反等数学思想,渗透直观想象、逻辑推理、数学抽象、数学运算等数学核心素养.
(2)教学方法
采用探究发现、讲授法为主、启发法为辅的教学方法.
三、教学过程
1.创设情境,激发兴趣
情境大家都知道诸葛亮吗?他是中国历史上杰出的政治家和军事家,被看作智慧的化身.一日,诸葛亮偶然间听到一句话:“三个臭皮匠,抵个诸葛亮”,作为当事人的他对此话深表怀疑,决定用事实推翻这句话.假设已知诸葛亮独自解出问题的概率为0.8,臭皮匠老大、老二、老三独自解出问题的概率分别为0.5,0.45,0.4,将三个臭皮匠中至少有一个人解出问题的概率与诸葛亮独自一人解出问题的概率作比较,谁的概率较大?
师:做概率题之前,一般先设事件.设三个臭皮匠中至少有一个人解出问题为事件D,老大、老二、老三独自解出问题分别为事件A,B,C.分析事件D,至少有一个人解出问题,分为哪几种情况?
生1:可以是一个人解出问题、两个人解出问题,或三个人都解出问题.
师:事件D较复杂!对于复杂的事件,本着“正难则反”的原则,由上一节学习的对立事件可列出什么式子?
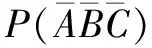
设计意图将俗语转化为数学模型,引起学生对旧知的主动复习,并充分调动学生认知结构中与本节课相关的知识点,发现部分问题不能解决,引发冲突,进而引出本节课要学习的内容.
2.初探新知,生成定义
问题1通过下面的两个试验,观察事件A的发生是否会影响事件B发生的概率?
问题2P(A),P(B),P(AB)之间存在什么数量关系?
试验1分别抛掷两枚质地均匀的硬币,A为“第一枚硬币正面朝上”,B为“第二枚硬币反面朝上”.
师:首先,直观感知,不论第一枚硬币是正面朝上还是反面朝上,都不会影响第二枚硬币的正反面,所以说这两个事件的发生是互不影响的.如何从定量的角度进行描述?
(教师为学生分发硬币,以5人为一个小组,分析讨论)
师:为了方便,用1表示硬币“正面朝上”,用0表示硬币“反面朝上”.刚才大家也投掷了硬币,发现样本空间Ω={(1,1),(1,0),(0,1),(0,0)};A={(1,1),(1,0)};B={(1,0),(0,0)};AB={(1,0)}.由上节课学习的古典概型,大家能求出事件A,B及AB的概率吗?其关系如何?

师:很好,观察力很强.那事件间互不影响和公式P(AB)=P(A)P(B)是否具有必然的关联?该公式是否具有普遍性?现在观察试验2,探究是否可得出同样的结论?
试验2一个袋子中装有标号分别为1,2,3,4的4个球,除标号外没有其他差异,采用有放回方式从袋中依次任意摸出两球.设A为“第一次摸到球的标号小于3”,B为“第二次摸到球的标号小于3”.
师:直观上,因为采用有放回的摸球方式,所以不论第一次摸到球的标号为多少,都不会对第二次摸球产生影响,也就是说这两个事件是互不影响的.接下来观察能否得出P(AB)=P(A)P(B)?
师:设样本空间Ω={(m,n)|m,n∈{1,2,3,4}}.因为采用有放回的摸球方式,所以m,n均可取1,2,3,4.故样本空间有16个样本点.
对事件A,有m<3,故A={(1,1),(1,2),(1,3),(1,4),(2,1),(2,2),(2,3),(2,4)};对事件B,有n<3,故B={(1,1),(1,2),(2,1),(2,2),(3,1),(3,2),(4,1),(4,2)};对交事件AB,有m<3,n<3,故AB={(1,1),(1,2),(2,1),(2,2)}.这三个事件的概率分别为多少?
师:最初对两个试验的感性认识为事件之间互不影响.对上述两个试验的共同属性进一步抽象概括,从定量的角度引入这种事件关系的一般定义:对任意两个事件A与B,如果P(AB)=P(A)P(B)成立,则称事件A与事件B相互独立,简称为独立.
设计意图通过两个试验的探究,对事件的相互独立性由感性认识上升到理性认识,得到事件的相互独立性的定义.
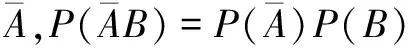

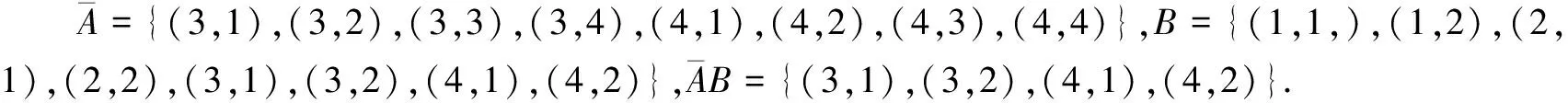
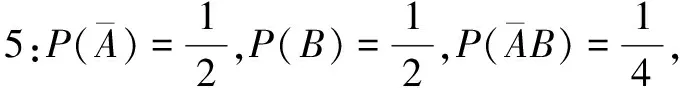
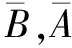

师:能否用今天学习的事件的相互独立性的定义对刚才的结论进行推理证明呢?

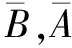

众生:利用类比思想,对于三个事件同样成立.

设计意图通过对试验3的探究得出如果事件A与B相互独立,则它们的对立事件也相互独立;再由类比思想推广到三个事件,为解决情境中抽象出的数学问题做铺垫.
3.解决疑问,德育渗透
师:学习了事件的相互独立性定义后,一起和诸葛亮解决他的疑问吧.
设计意图呼应课堂伊始的情境.一方面,学生利用所学新知解决问题,获得成就感;另一方面,通过对情境问题的解决,对学生进行德育渗透.
4.课堂小结,观点提炼
师:请同学们回顾并总结本节课学习的内容.

师:非常好.本节课的一个中心思想是复杂事件简单化,对于复杂事件,由正难则反的思想,利用对立事件可轻易地将其简单化.这就是我们本节课学习的全部内容.
设计意图学生进行课堂总结,不仅有利于培养学生的归纳概括能力,而且有利于了解学生是否掌握本节课所学内容.值得注意的是,对于学生没有想到的思想方法,教师要及时补充.
5.布置作业,及时巩固
(1)除了“三个臭皮匠,抵个诸葛亮”这句谚语,“智者千虑必有一失”、“不要把鸡蛋放在同一个篮子里”这两句谚语也包含了今天所学的内容,能否用今天所学的知识对其进行解释?
(2)事件的相互独立性除了在谚语中有所体现,在生物学中也有所运用,比如大家熟知的孟德尔遗传规律.阅读课本第259页“阅读与思考”栏目中的内容,了解孟德尔遗传规律与本节课所学内容的关系.
