教材整合显自然 数学探究育素养——以“等式性质与不等式性质”教学为例

石雨卓

(浙江省诸暨中学暨阳分校,311800)

随着《普通高中数学课程标准(2017年版2020年修订)》[1](以下简称课标)的颁布和实施,新教材提供了问题情境、探究活动、例题练习等丰富的教学资源,并将这些资源组成一个紧密联系的有机整体,为教学实践提供了范本.因此,教师应当比较新旧教材,深入研读课标和教材,挖掘新教材的编写意图,并根据学生实际情况,灵活使用教材,取长补短,合理整合,让课堂教学更加自然流畅.本文以“等式性质与不等式性质”第1课时教学为例，对此进行探究．

一、新旧教材比较分析

从授课时间段、知识点、教材结构这三个角度研究新旧教材“等式与不等式性质”的内容差异,得到如下表1[2].

结合新旧教材分析,发现新教材将“等式性质与不等式性质”这一部分内容提前至高一上学期学习,承接学生初中已学的关于等式与不等式的基础知识,引导学生类比等式研究不等式,并为之后学习函数单调性等性质做好铺垫,形成函数、方程与不等式的结构和系统,起到承前启后的作用.对比旧教材中必修五第三章的位置,新教材此次调整显然在学生的思维逻辑上更为合理,整体设计更显自然.

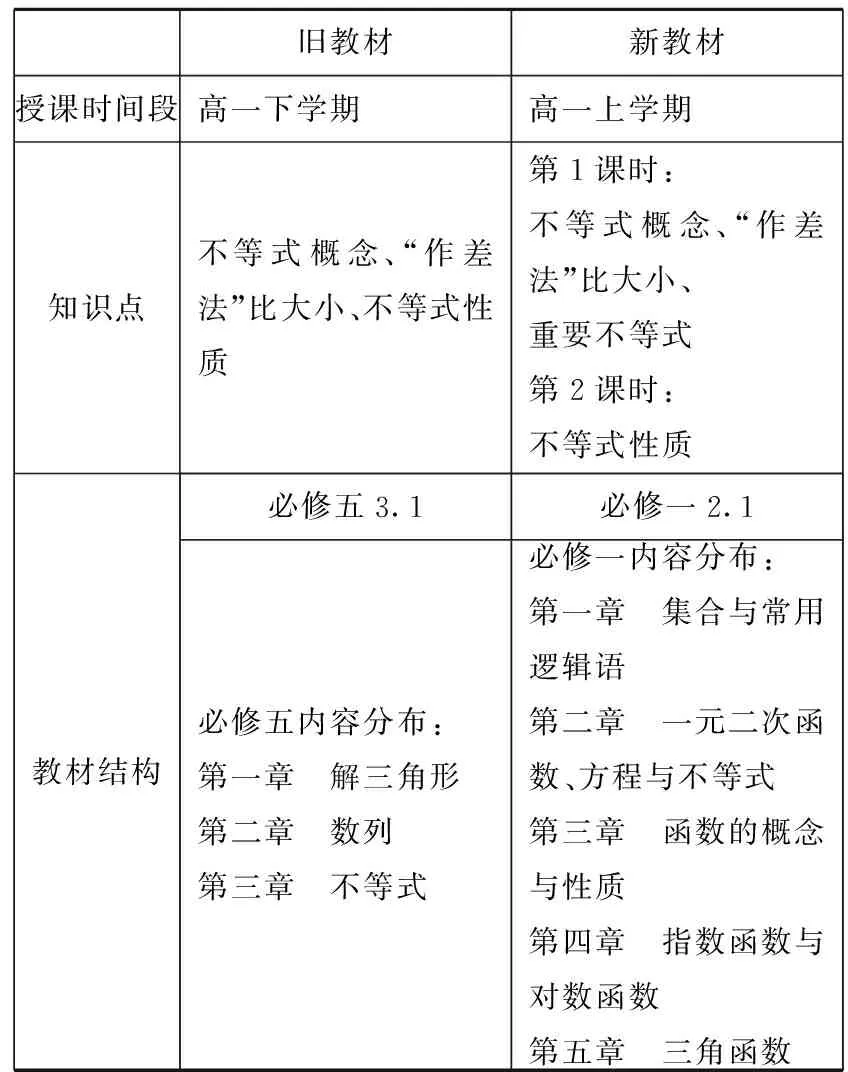
表1 新旧教材“等式与不等式性质”比较表

在内容上,旧教材并未明确划分课时,主要从情境中抽象出不等式,从“数轴法”比较实数的大小中引出“作差法”比较大小,以此作为研究不等式的一个出发点,得到不等式的性质,最后是不等式性质的简单应用,具体流程见图1.主要强调“不等式”的工具作用及应用价值.

而新教材则明确将本节课划分为两个课时:第1课时为从情境中抽象出不等式,从研究不等式性质引出基本事实并进行“作差法”应用,最后从赵爽弦图中得到重要不等式(见图2);第2课时则主要从等式的性质中类比得到不等式性质,旨在帮助学生学会类比学习的学习方法,完成初、高中学习的过渡.

二、教学设计

结合教材、学情及实践综合分析,可对教学内容进行整合,将赵爽弦图的探究移至“作差法”比较大小前面，不仅从情境中发现不等关系,还从赵爽弦图(图形)中发现相等关系和不等关系,尤其是重要不等式的挖掘,自然过渡到用作差法来证明该不等式,体会数形结合思想的应用.具体流程设计如图3所示.

教学过程如下：

1.情境引入

现实生活中存在大量的相等关系和不等关系,如何用数学语言抽象表达这些关系?请看教材第37页的问题1.

问题1(具体内容略).

设计意图学生从现实、科学、数学等情境中挖掘出不等关系,并用不等式加以表述,最后总结如何用不等号等符号语言来表达情境中关于不等关系的文字语言,体会数学抽象的核心素养,感悟“数学来源于生活”,最后总结不等关系的文字语言与符号语言的转化(见表2).

表2

2.新知探究

问题2上面从实际情境中抽象出不等关系,能否在图形中也抽象出不等关系呢?结合中国古代数学家赵爽设计的弦图(如图4),你能从图中发现哪些相等关系和不等关系?

生1:图4中有四个全等的直角三角形和两个正方形，由S大正方形≥S小正方形得c2≥(a-b)2由S大正方形=S小正方形+4SRt∆ABE得c2=(a-b)2+2ab，即我们熟知的勾股定理c2=a2+b2.

生2:除了S大正方形≥S小正方形,我还发现S大正方形≥4SRt∆ABE,即c2≥2ab.由勾股定理得a2+b2≥2ab.

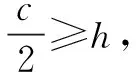
(同学们结合图形,从边长、角度、周长、面积等方面提出众多相等和不等关系,限于篇幅,此处不一一列举)

师:我们从图形角度证明了当a>0,b>0时,上述不等式成立,能否从代数的角度来加以证明呢?本节课以a2+b2≥2ab为例进行论证.

生:由a2+b2-2ab=(a-b)2≥0,证得a2+b2≥2ab.

追问:当且仅当a，b满足什么条件时,不等式取到等号.

生:从代数推导过程中发现当且仅当a=b时,不等式取到等号.

教师再借助GGB演示,引导学生从几何角度加以补充说明:当且仅当a=b时,中间小正方形面积为0,则S大正方形=4SRt∆ABE,即a2+b2=2ab.

追问:若去掉“当a>0,b>0”这一条件,结论是否仍然成立?

生:回顾上述证明过程,此结论仍然成立.

由此总结:

(1)重要不等式:a2+b2≥2ab(a，b∈R).

(2)利用作差法比较两个代数式大小:

① 基本事实:

a-b>0⟺a>b

a-b=0⟺a=b

a-b<0⟺a

② 基本步骤:

设计意图在情境引入后对赵爽弦图的探究,不仅从图形中抽象出不等关系,体会数形结合的数学思想,还可以发展数学抽象的核心素养,更从数学史中感悟数学文化的魅力.接着从弦图的几何证明,自然过渡到代数证明,引出“作差法”比较代数式大小.

3.新知应用

例1已知a>0,b>0,比较a3+b3与ab2+a2b的大小.

生1:(a3+b3)-(ab2+a2b)=a3-a2b+b3-ab2=a2(a-b)+b2(b-a)=(a-b)(a2-b2)=(a-b)2(a+b)，∵a>0,b>0,∴(a-b)2≥0,(a+b)>0,∴(a3+b3)-(ab2+a2b)≥0,即(a3+b3)≥(ab2+a2b).

生2:(a3+b3)-(ab2+a2b)=a3-ab2+b3-a2b=a(a2-b2)+b(b2-a2)=(a-b)(a2-b2)=(a-b)2(a+b).

生3:(a3+b3)-(ab2+a2b)=(a+b)(a2-ab+b2)-ab(a+b)=(a+b)(a-b)2.

例2在现实生活中,当我们觉得一杯咖啡太苦时,会通过加糖使其变甜,请你用不等式来表述这一关系,并进行证明.

设计意图通过例1及其变式,从不同角度对不等式加以证明,拓宽学生的思维,加深对“作差法”的理解.同时结合对“糖水加糖”模型的改编,感悟“数学来源于生活,应用于生活”这一理念.最后通过严谨的数学证明,发展逻辑推理核心素养,培养数学创新意识和实践能力.

4.课堂总结

5.作业布置

请证明你在赵爽弦图中发现的其他等式与不等式,并尝试在生活中找出相应情境来刻画这些等式与不等式.

三、教学反思

1.教材整合显自然

在新课标的视角下,新教材比旧教材更加注重发展学生学科核心素养和“以生为本”的主体意识.但是“书不尽言,言不尽意”,作为教师,应当认识到教材是为教学工作服务的,教学是“用教材”而不是“教教材”.所以需要教师充分挖掘教材,注重数学知识间的联系与发展.教师应结合学生实际情况,对教学内容进行“再加工”,将数学知识编成学生喜爱且参与度高的“课堂剧”,从而彰显数学知识生成的“自然”,引导学生经历知识的自然生成,领悟数学的本质.

2.数学探究育素养

本节课从情境中的不等关系过渡到图形中的不等关系,再由此挖掘出重要不等式,并利用“作差法”加以证明,最后应用所学知识来刻画生活中的不等关系,并给出证明.在探究活动中,学生以学习主体的身份全程参与知识的产生、发展和应用,不仅接受了数学知识本身,更在过程中积累了“基本活动经验”.在教学过程中,不仅有师生探究、生生探究,还有学生 “独立探究”,学生有足够的课堂思考交流的时间和空间,提升了学生数学抽象、逻辑推理等学科核心素养.