关注高考数学新题型“多选题”之导数部分

江苏省外国语学校（215100）何 慧

高考数学选择题出现新题型“多选题”，这比以前的“单选题”增加了难度，不便于直接运用排除法迅速获解。基于此，笔者对导数部分“多选题”进行归类解析，以便学生熟悉新题型，增强解题体验，不断积累解题经验。

类型一、以“多选题”的形式考查函数的极值点

［例1］（多选题）（2021 年北京师大附中期中考试试题）下列函数中，存在极值点的是（ ）。

对于选项B，函数y=根据指数函数的图像与性质，当x<0 时，函数y=2|x|单调递减，当x>0 时，函数y=2|x|单调递增，所以函数y=2|x|在x=0处取得极小值。

对于选项C，函数y=−2x3−x，则y′=−6x2−1 <0，所以函数y=−2x3−x在R 上单调递减，没有极值点。

综上，应选B，D，E。

评注：一般地，分析f(x)是否存在极值点，不是考查方程f′(x)=0是否有解，而是考查导函数在某点附近左右两侧的单调性是否相反，即考查导函数是否存在变号零点。

类型二、以“多选题”的形式考查导函数的图像与函数的性质

［例2］（多选题）（2021 年山东省日照实验高级中学阶段性考试试题）函数y=f(x)的导函数y=f′(x)的图像如图1 所示，以下命题错误的是（ ）。

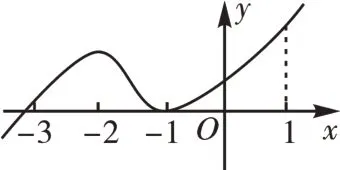
图1

A.−3是函数y=f(x)的极值点

B.−1是函数y=f(x)的最小值点

C.y=f(x)在区间(−3,1)上单调递增

D.y=f(x)在x=0处切线的斜率小于零

解析：根据导函数的图像可知，当x∈(−∞,−3)时，f′(x) <0，在x∈(−3,1)时，f′(x) >0，所以函数y=f(x)在(−∞,−3)上单调递减，在(−3,1)上单调递增，则x=−3是函数y=f(x)的极值点。

因为函数y=f(x)在(−3,1)上单调递增，所以−1不是函数y=f(x)的最小值点。

因为函数y=f(x)在x=0 处的导数大于0，所以y=f(x)在x=0处切线的斜率大于0。

综上，命题错误的选项为B，D。

评注：以图为载体考查导数的应用，解题切入点是认真观察图形特点。

类型三、以“多选题”的形式考查函数的单调性与极值

［例3］（多选题）（2020 年山东省泰安第二中学月 考题）设f′(x)为函数f(x)的导函数，已知

评注：本题还可以灵活运用特例法获解。取适合题意的函数f(x)=2，则易知A，B 错误，又多选，故选C，D。

类型五、以“多选题”的形式考查导数的应用

［例5］（多选题）（2021 年北京师大附中试题）设函数f(x)=

则函数g(x)（即xf(x)）在()1,+∞上单调递增，在（0，1）上单调递减。故函数g(x)（即xf(x)）的极小值为g(1)=f(1)=故选A，B，C。

评注：本题的解题关键是准确分析函数xf(x)的单调性和极值，从而需要考虑导数的运算法则。对题设条件x2f′(x)+xf(x)=lnx进行适当变形，有利于问题的分析与求解。，则下列说法正确的是（ ）。

A.f(x)定义域是(0,+∞)

B.x∈(0,1)时，f(x)图像位于x轴下方

C.f(x)存在单调递增区间

D.f(x)有且仅有两个极值点

E.f(x)在区间（1，2）上有最大值

类型四、以“多选题”的形式考查导函数与不等式的交汇

［例4］（多选题）（2020 年山东省济南市章丘区试题）定义在(0,+∞)上的函数f(x)的导函数为f′(x)，且(x+1)f′(x)−f(x)

因为(x+1)f′(x)−f(x)g(2)>g(3)，整理得2f(2)−3f(1) <5，f(3)−2f(1) <7，故A错误，C正确。

据此可知，f(x)存在单调递增区间，故选项C正确；f(x)有且仅有1 个极小值点，故选项D 不正确；f(x)在区间（1，2）上先减后增，没有最大值，所以选项E不正确。

综上，应选B，C。

评注：本题还可以借助数形结合法加以巧解。先根据导数分析函数的性质，再画出函数的大致图像，最后观察图像即可确定结论。

类型六、以“多选题”的形式考查导数与其他知识的综合运用

［例6］（多选题）（2020 年山东省枣庄市高三训练题）关于函数f(x)=+lnx，下列判断正确的是（ ）。

A.x=2是f(x)的极大值点

B.函数y=f(x)−x有且只有1个零点

C.存在正实数k，使得f(x)>kx恒成立

D.对任意两个正实数x1，x2，且x2>x1，若f(x1)=f(x2)，则x1+x2>4

设函数h(x)=x−xlnx−4（x>0），则h′(x)=−lnx，易知函数h(x) 在(0,1) 上单调递增，在(1,+∞)上单调递减，所以h(x) ≤h(1)=−3 <0，g′(x) <0，函数g(x)在(0,+∞)上单调递减。又当x→+∞时，g(x)>0且g(x) →0，所以根据（∗）式可得k≤0，这显然与k为正实数矛盾。故不存在正实数k，使得f(x)>kx恒成立，故选项C错误。

（4）由（1）知，f(x)在(0,2)上单调递减，在(2,+∞)上单调递增，x=2 是f(x)的极小值点。由于任意两个正实数x1，x2，且x2>x1，f(x1)=f(x2)，故0

由于t>1，则tlnt>0，故证2t2−2 −4tlnt>0(t>1（)∗∗）。

综上，应选B，D。

评注：本题设计较好，侧重考查由导数知识求解函数的极值点、零点问题以及函数与不等式的综合问题，其中选项C，D 难度较大，对学生分析与解决问题的能力有较好的考查。