导数中指数式与对数式的处理技巧
2022-11-27广西南宁市第三中学530021
广西南宁市第三中学(530021)刘 辉
导数是研究函数图像和性质的重要工具,也是高考数学的重点和难点内容。导数的教学不仅可以培养学生的运算能力,训练学生分析问题和解决问题的能力,还可以渗透函数与方程、转化与化归、数形结合、分类讨论等数学思想。由于导数解答题中的函数结构复杂,常含有指数式或对数式等超越式,常需高深的构造函数或运算的技巧,有时还需要进行多次含参讨论,让不少学生找不到解题的突破口。当函数中含有指数式或对数式等超越式时,可以采用“团结指数”“孤立对数”“指对分离”“利用同构”“适当放缩”等解题技巧。文章以一些典型问题为例,讲解这五种技巧,为学生提供明确清晰的解题思路。
一、团结指数
如果一个函数由指数式ex和多项式构成,则通常将函数转化为形如h(x)·ex或h(x)·e−x的形式,由于(ex·h(x))′=ex(h(x)+h′(x)),(e−x·h(x))′=e−x(−h(x) +h′(x)),ex为正数,导数只要正负,求导后就不需要再研究指数式了,此时问题就简化为研究多项式h(x)和h′(x)的正负情况,进行分类讨论即可求解。这种将ex或e−x与多项式乘在一起当作新函数来研究的方法,称为“团结指数”。
[例1](2020 年全国Ⅰ卷第21 题第2 问)已知函数f(x)=ex+ax2−x。当x≥0 时,f(x) ≥求a的取值范围。
问题1:本题属于导数中的哪种类型?这类问题有哪些常见解法?
由题意可得,ex≥,本题属于不等式恒成立问题,最常见的解法有分离变量法和直接求导分类讨论法。分离变量法的解题思想是将“含参”问题转化为“无参”问题,本题可以利用这种方法求解,但运算量较大,对学生的计算能力要求极高。若直接作差、求导,再分类讨论,导数中仍含ex和多项式,且含有参数,看不出导数的正负,也不可以分解因式,没办法进行讨论。
问题2:分类讨论法用不了,分离变量法计算又太繁杂,我们应从哪个角度思考呢?

这里注意到x≥0,e−x>0,故只需要讨论(x−2a−1)(x−2)的符号情况。
问题3:这种与二次函数有关的导数题目,分类讨论的标准是什么?
通常比较导数等于0 的两根的大小,还要拿这两根与区间的端点值进行大小比较,因此2a+1 既要和2进行大小比较,也要与0进行大小比较。
(1)当2a+1 ≤0,即a≤时,当x∈(0,2)时,g′(x) >0,故g(x)在(0,2)上单调递增,此时g(x) >g(0)=1,不符合题意。
(2)当0<2a+1<2,即时,x∈(0,2a+1)时,g′(x) <0,g(x)单调递减;x∈(2a+1,2)时,g′(x) >0,g(x) 单调递增;x∈(2a+1,+∞) 时,g′(x) <0,g(x)单调递减。

总结:本题考查利用导数研究函数的单调性和最值,考查学生分析问题和解决问题的能力。教师应引导学生掌握本题中转化函数结构的背景:当指数式ex和多项式同时出现时,常转化为ex或e−x与多项式乘积的结构。另外,也需要学生总结不等式恒成立问题的各种处理方法,以及含参分类讨论的标准,做到学一题、得一法、会一类。
二、孤立对数


当0
问题2:这种不等式问题,一般先求导,再研究单调性即可,大家试一下,过程中会遇到什么障碍?
如果我们把分子当成一个新函数y=2xlnx+(k−1)(x2−1),求导,得y′=2(1+lnx)+2(k−1)x,导数会带有lnx,且含有参数k,不易处理,若再次求导,二阶导数中仍有参数,且看不出正负。
问题3:这种情况下,如何对函数变形?


总结:当函数结构中含有对数式和多项式时,可以适当使用“孤立对数”这一技巧,求导后不再含有对数式,可以简化导数的结构,降低问题的难度。实际上,“团结指数”“孤立对数”等本质是一样的,都是通过处理,使导数结构中不含指数式或对数式。
三、指对分离
在不等式证明中,如果同时出现ex与lnx,求导后含有超越式,且多次求导后也看不出正负,就可以考虑将指数式和对数式分开,分别研究两个函数的最值,从而解决问题。这种将指数和对数分开,研究两个函数的方法称为“指对分离”,一般适用于含指数式和对数式的不等式证明。

问题1:如何证明一个函数大于0?

问题2:能否尝试对函数结构进行变形?
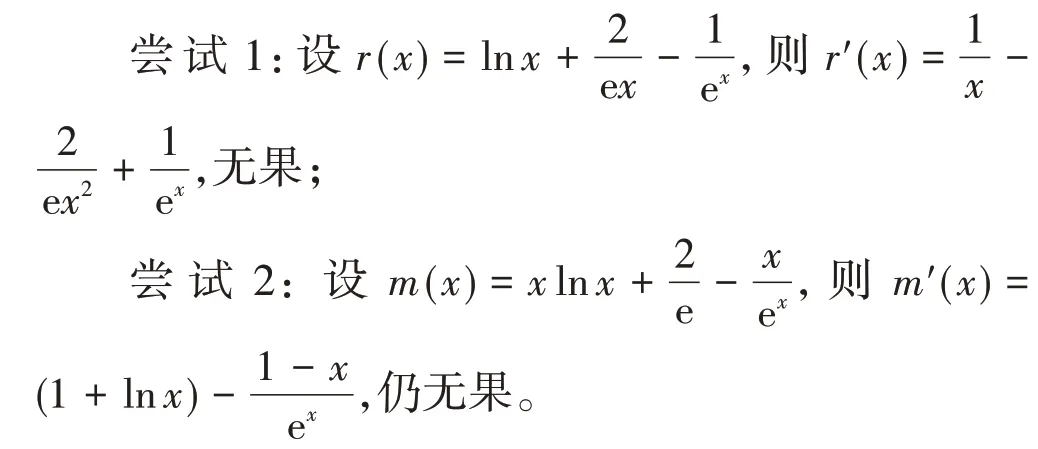
问题3:观察前两个尝试,合在一起无法处理,将函数分开成两个会怎样?
注意到m′(x)=(1+lnx) −,若分开成两部分,很容易看出这两个函数的极值点。

总结:在指数与对数同时出现的不等式证明中,如果直接求导或多次求导仍无法得证,就可以考虑将指数和对数分开,变成两个函数,分别研究两个函数的最值。在证明过程中,要适当乘上或除以多项式进行调整。一般是一个函数的最大值小于或等于另一个函数的最小值,由于满足的条件较为苛刻,因此“指对分离”这个技巧一般适用于含指数式和对数式的不等式证明,在求参数范围时很少用。另外,ex,lnx,x这三者之间通过乘或除构成的函数的单调性、最值或图像,我们也要非常熟悉。
四、利用同构
为了达到不等式两边“结构”相同的目的,常需对“指对式”进行“改头换面”,如x=elnx,xex=elnx+x,通过转化,构造出结构相同的式子,再构造函数,利用新函数的单调性求解,这种方法称为“利用同构”,通过同构,可将复杂的函数结构变简单,降低问题的难度。
[例4](2020 年山东高考第21 题第2 问)已知函数f(x)=aex−1−lnx+lna,若f(x) ≥1,求a的取值范围。
问题1:由题意得aex−1−lnx+lna≥1,这个不等式结构有什么特点?
不等式中既有指数又有对数,不适合使用“指对分离”的技巧,求导后仍是超越式,直接求导也无法得解,需要仔细观察函数结构,寻求转化。
问题2:尝试一下,看看如何转化?
注意aex−1=ex−1+lna,原不等式转化为elna+x−1−1+lna≥lnx,两边同时加上x上后可得elna+x−1+x−1+lna≥x+lnx,elna+x−1取以e 为底的对数就是x−1+lna,这样构成了左右两边结构相同的式子,再构造新函数,利用不等式求解,这就是“利用同构”法。
解:由f(x)=aex−1−lnx+lna≥1 移项得aex−1+lna≥lnx+1,即elna+x−1+lna≥lnx+1,两边同时加(x−1)得elna+x−1+x+lna−1 ≥lnx+x,即elna+x−1+(x+lna−1) ≥lnx+elnx,
设g(x)=x+ex,则g′(x)=1+ex>0,所以g(x)单调递增,所以lna+x−1 ≥lnx,即x−lnx+lna−1 ≥0,
设h(x)=x−lnx+lna−1,则h′(x)=1 −所以h(x)在(0,1)上单调递减,在(1,+∞)上单调递增,所以h(x)min=h(1)=lna≥0,所以a≥1。
五、适当放缩
在导数的学习中,我们需要熟练掌握一些常见的不等式,如x>0 时, 问题1:对于这个不等式,你有什么想法? 题目中既有指数式ex,又有三角函数sinx,还有对数式,直接求导不易处理,如果能得关于ex和sinx的常见不等式就可以通过放缩法简化函数结构,降低问题难度。 问题2:关于指数式ex和三角函数sinx的常见不等式,你最容易想到什么? 想到泰勒展开式,利用泰勒展开式可以得关于ex和sinx的常见不等式。 解:要证明ex+sinx>xlnx+1,可对不等式左边进行放缩, 总结:适当放缩,可以快速将指数式或对数式这两种超越式与多项式建立联系。但放缩法对学生的能力要求很高,需要学生熟练掌握很多常见不等式和熟悉各种函数结构组合后的特点。在教学中,教师要做好引导,通过不同的放缩来拓展学生的视野,开阔学生的思路,同时也要注重充分展示学生的思维成果,鼓励学生大胆尝试,让学生乐于放缩,享受“放缩”带来的快乐。 综上所述,对于含有指数式或对数式的导数题目,通过团结指数、孤立对数、指对分离、利用同构、适当放缩这五种技巧,可以简化函数结构,减少讨论,降低问题的难度。学生要对函数进行分析,观察函数的具体特征,研究函数的结构,将复杂的函数转化为合适的函数,并有针对性地选择解题方法,总结解题思路,提高解题水平。


