基于改进C4.5算法的退役动力电池等级筛选研究
2022-11-26宋汶秦王海亮赵春娟王兴贵
宋汶秦,王海亮,赵春娟,王兴贵
(1.国网甘肃省电力公司经济技术研究院,甘肃兰州 730000;2.兰州理工大学电气工程与信息工程学院,甘肃兰州 730050)
随着能源紧张与环境恶化,研究并利用电动汽车相关技术,推进该产业发展已成为全国汽车行业互相竞争的新焦点[1]。电动汽车的动力电池在使用一段时间后需要进行退役处理,并更换新电池以保证电动汽车的运行安全性与续航能力[2]。《节能与新能源汽车产业发展规划(2012—2020 年)》中指出:电动汽车的供应量仍将保持增加趋势,由此产生的能源缺乏和环境污染问题将更加严峻[3]。如果退役动力电池处理不当,将会对环境造成严重污染。国务院办公厅印发的《新能源汽车产业发展规划(2021—2035 年)》专栏3《建设动力电池高效循环利用体系》中明确指出:支持电动汽车动力电池梯次产品在储能、备能等领域创新应用,加强余能检测、残值评估、重组利用、安全管理等技术的研发[4]。
退役的动力电池仍有80%的储能价值可以利用[5]。绿色和平、中华环保联合会共同发布《为资源续航:2030 年新能源汽车电池循环经济潜力研究报告》中指出:在国内,若80%的退役动力电池被梯次利用市场所吸纳,到2030 年退役电池总价值将接近430 亿人民币,这可以给动力电池回收再利用产业链带来更多的机遇[6]。因此,若将其直接进行报废处理,必然会造成极大的能量浪费。为充分利用电动汽车退役动力电池的剩余价值,可将其应用于电网储能电站、新能源发电、低速电动汽车、光伏路灯等不同领域,实现梯次利用[7]。动力电池在电动汽车中使用一定时间后,其外观、容量、内阻等方面会表现出较大的不一致性。如果在梯次利用前对其不进行分类,势必会造成能源的浪费、电池的过充及过放甚至爆炸等危险。因此,对退役动力电池在梯次利用前进行等级筛选具有重要的意义。目前,传统的筛选技术主要采用充满-放空(full charge-discharge,FCD)方法,该方法筛选效率较低。有学者通过对比单体电池充放电曲线的紧密程度来判断其性能的近似程度,以提高电池筛选的一致性[8]。为改善分选的不一致性,常用的方法还包括支持向量机、神经网络、模糊C均值及改进k-means 聚类等方法[9]。
以智能算法为基础的等级筛选方法可以解决大范围退役动力电池的分类。本文研究一种基于改进C4.5 算法的退役动力电池等级筛选方法。首先,根据退役动力电池的梯次应用场合确定等级类型并将其作为筛选决策树的叶子节点;然后,结合对数函数的麦克劳林展开式对特征属性的信息增益率计算过程进行简化;最后,构建退役电池等级筛选决策树,并通过实例仿真对传统C4.5 算法及其改进算法在退役电池等级筛选中应用的精确性与执行效率进行对比分析。
1 C4.5 决策树算法及其改进
决策树(decision tree)是通过一组或多组无规则、无顺序的实例数据来推理、归纳出分类规则的一种机器学习分类算法模型[10]。决策树中包含根节点、叶子节点和非叶节点。根节点是树最顶层的节点;叶子节点代表类别;非叶子节点代表一个或多个特征属性,用于确定数据样本的分支[11]。
1.1 C4.5 算法的基本原理
ID3 算法是决策树中较为常用的算法,该算法以信息增益为准则对最优属性进行划分[12]。但是,该算法存在对可取值数据较多的属性有所偏好的问题。为解决该问题,有学者以ID3 算法为基础,提出了C4.5 算法[13]。该算法在确定决策树内部分支特征属性时用信息增益率取代传统的信息增益,在等级分拣过程中,具有规则通俗易懂,精确率较高的优点[14]。C4.5 算法流程如图1 所示。
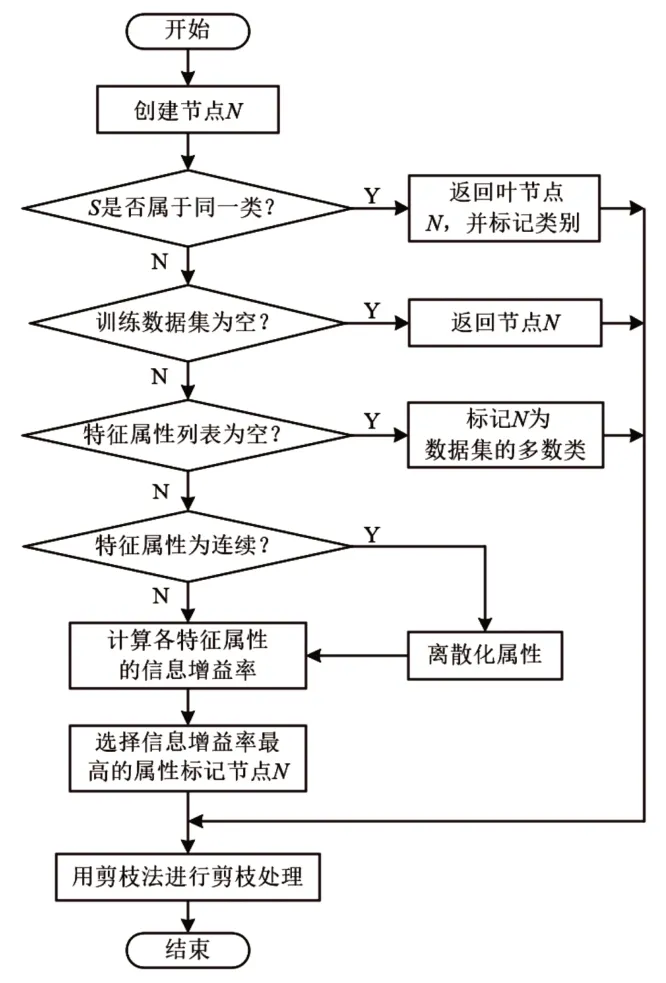
图1 算法流程图
1.2 基于改进C4.5 算法的等级分类决策树模型
在建立基于C4.5 决策树算法的退役动力电池等级筛选模型时,需要通过大量对数运算得到各属性的信息增益率以判断最优的分支。这很大程度上削减了算法的运行速度,降低了执行效率。
针对该问题,在计算过程中引入对数函数的Maclaurin 展开式对其进行简化。ln(x+1)的麦克劳林展开式如式(1):
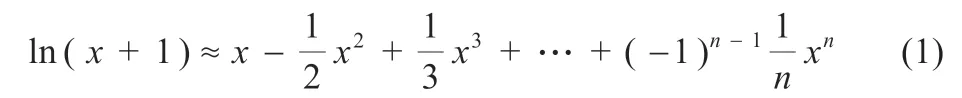
以改进C4.5 决策树算法在电动汽车退役动力电池等级筛选中的应用研究为例进行概述。假设退役动力电池数据样本集S的容量大小为D。等级类型用Ck(1 ≤k≤n)表示,n为类型的个数,则该数据样本分类的信息熵为:
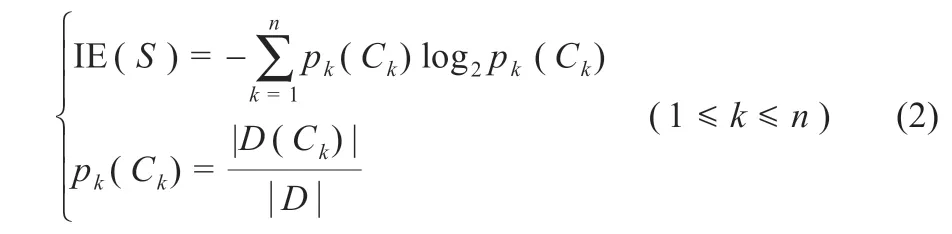
式中:D(Ck)为数据集S中属于类型Ck的容量大小;pk(Ck)为第k个类别Ck在数据集S中出现的概率。
令pk(Ck) -1=P,结合式(1),数据集S的信息熵为:
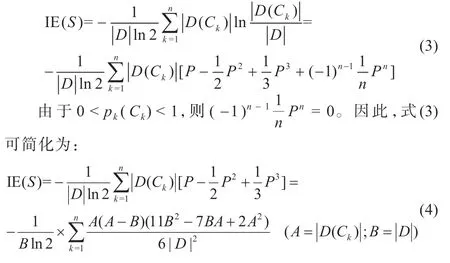
设退役动力电池特征属性Ai(1 ≤i≤M)有M个不同的取值,根据属性Ai将S进行状态划分Ai_j(j=1,2,...,N)。特征属性Ai的状态子集信息熵为:
由式(4)减去式(5),可以获得各特征属性Ai的信息增益量:
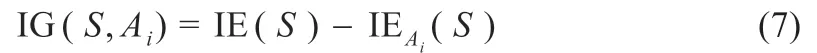
特征属性Ai的固有值,即分类信息为:
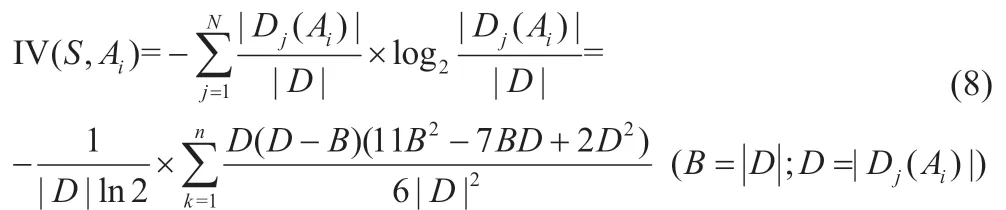
从式(8)可以得出,特征属性Ai划分的状态越多,其固有值越大。由式(7)和(8)可得到特征属性Ai的信息增益率:
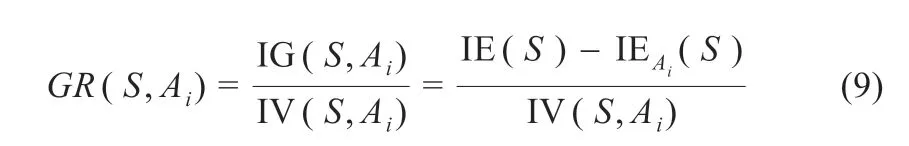
各属性Ai的重要程度用信息增益率GR(S,Ai)来衡量,而且Ai的重要程度与“信息增益率”成正比,并选择GR(S,Ai)大的Ai作为决策树的分裂属性。
2 退役动力电池等级筛选流程
以退役动力电池训练数据集S作为样本集,在该样本集不断分裂形成退役动力电池等级分类决策树的同时,计算各特征属性的信息增益率,并选择信息增益率大的退役电池属性作为分枝节点。如此重复,可将退役动力电池样本集S分成n个样本子集。若样本子集的退役动力电池类别相同时,当前节点作为等级筛选决策树的叶子节点,分裂结束;若退役动力电池的样本子集中还存在不同的类别,则再次使用上述方法依次递归生成等级筛选决策树,直到所有退役动力电池的样本子集中包含的元素均属于同一个类别为止。算法的具体步骤如下:
输入:退役动力电池数据训练样本集S,退役动力电池特征属性集合Ai_list,决策特征属性Ai。
输出:退役动力电池分类决策树。
(1)以退役动力电池分类决策树样本集合S作为根节点N,创建等级分类决策树。
(2)若退役动力电池属性集S中所有的样本属于同一等级,则N为叶子节点,并标记等级Ck;否则,转步骤(3)。
(3)判断退役动力电池特征属性集合A_list 是否为空;如果A_list 为空,记节点N为退役动力电池训练样本S中含样本数量最多的类别Ck;若A_list 不为空,则转步骤(4)。
(4)采用改进C4.5 信息增益率方法计算属性列表A_list 中各特征属性Ai的信息增益率GR(S,Ai)。将GR(S,Ai)最大的Ai作为分割特征属性,并标记节点。根据该分割属性的状态划分Ai_j,确定训练子集Ai_list,然后建立分支。
(5)重复步骤(2)~(4),对所划分的样本子集生成新的退役动力电池特征属性决策分支,直到所有子集划分完为止。具体流程如图2 所示。
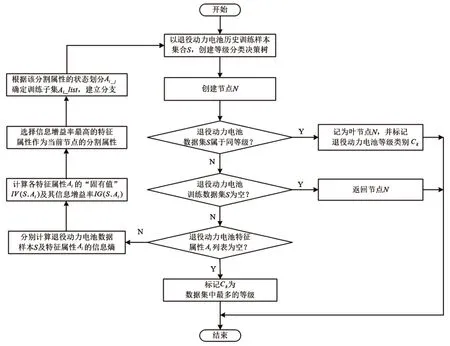
图2 退役动力电池等级筛选流程图
为得到一个合适的等级筛选模型,在具体训练过程中,采用K折交叉验证法(K-fold cross validation,K-CV)对所建筛选模型进行优化。将S中(K-1)个子集作为训练集,剩余1个作为测试集。该方法可使每个样本有均等的概率被用于训练和验证,在一定程度上能提升模型的泛化能力。
3 实验仿真结果分析
以电动汽车退役锂电池为研究对象进行分析。根据退役动力电池的性能指标,本文选择外观特性A1、电池容量A2、电池内阻A3作为决策树的特征属性,即M=3。各特征属性的状态划分如表1 所示。
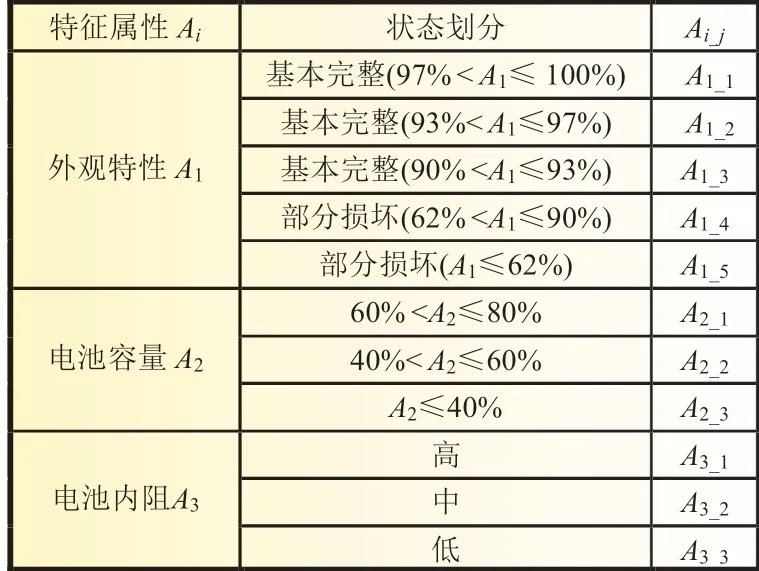
表1 各特征属性Ai 及状态划分Ai_j
根据退役动力电池的梯次利用范围将其等级划分为4类,如表2 所示。使属于等级1 的退役动力电池应用于电网储能电站或新能源发电;属于等级2 的退役电池应用于家庭能源、路灯等场合;对属于等级3、等级4 的退役电池修复后再次利用或者进行回收处理。
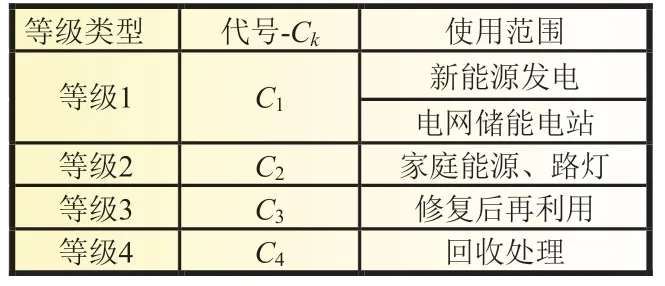
表2 等级划分Ck及梯次使用范围
采用改进的C4.5 算法训练退役动力电池筛选决策树时,典型数据集S中有240 个样本,随机选取其中200 个作为训练样本,40 个作为测试样本。采用改进的C4.5 算法训练退役动力电池筛选决策树。在训练过程中,采用K-CV 分析叶子节点Ck含有最小样本数对筛选决策树性能的影响,以对其进行优化,仿真结果如图3 所示。
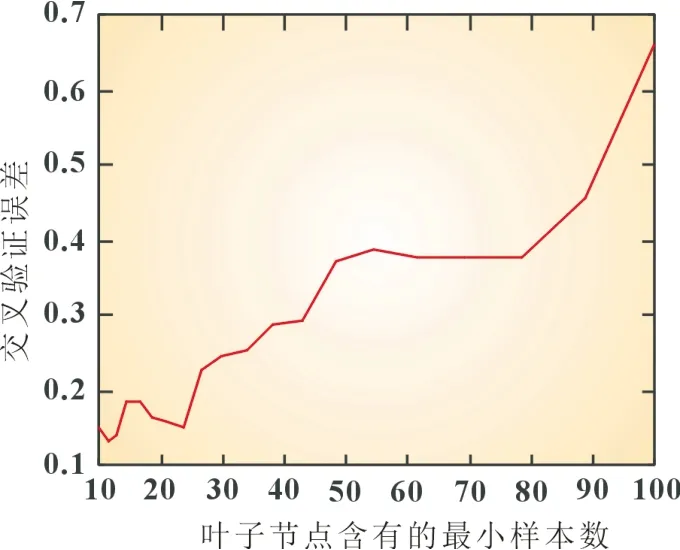
图3 叶子节点含最小样本数对其性能的影响
由图可知,叶子节点含有最小样本数为12 时,交叉验证误差最小,故选择minleaf 为12。通过优化得到的退役电池等级筛选决策树如图4 所示。由测试集对图4 中等级筛选决策树进行验证,得到等级1、等级2、等级3、等级4 的准确率分别为91.11%、100%、96.92%、90.625%。由此可知,其准确率较高。
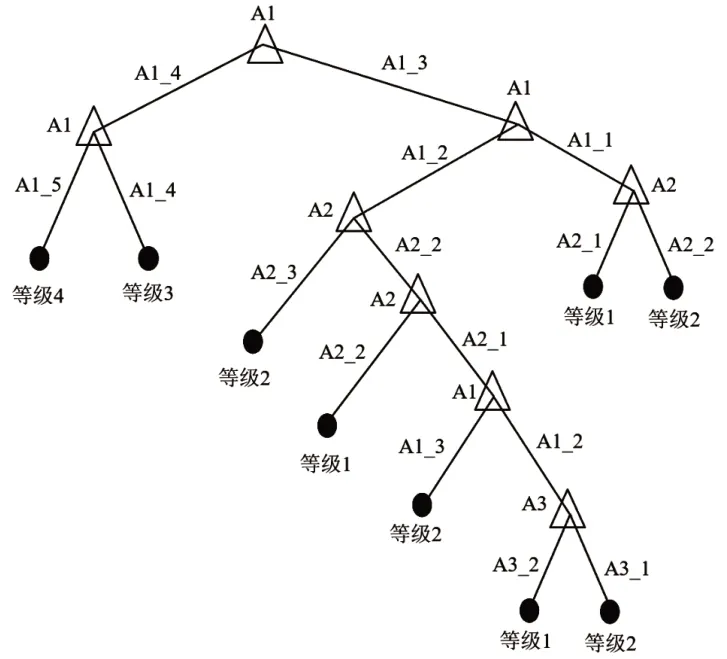
图4 退役动力电池等级筛选决策树
为进一步验证其准确性,在退役动力电池数据集S相同的情况下,分别对传统C4.5 算法与其改进算法的精确性和执行效率进行了对比分析,结果如图5 所示。
由图5 可知,相较于传统的C4.5 算法,采用改进的C4.5算法进行退役动力电池等级筛选时,算法执行效率较高。而且,改进C4.5 算法在提高算法执行时间的同时对筛选决策树等级分类的准确性影响较小。
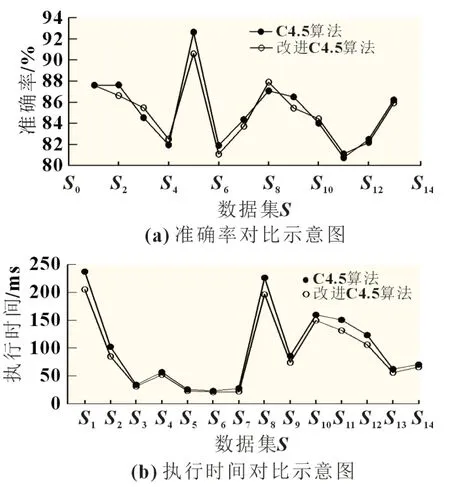
图5 传统C4.5与其改进算法对比示意图
4 结论
为实现退役动力电池的梯次合理利用,本文研究了基于改进C4.5 决策树算法的退役动力电池等级筛选方法。以退役动力锂电池的数据集对该方法的精确性和有效性进行了验证。主要有以下特点:
(1)在训练退役动力电池决策树过程中,采用K-CV 法分析了退役动力电池决策树叶子节点Ck含有的最小样本数对其性能的影响,选取交叉验证误差最小时minleaf 的值对等级筛选决策树进行了优化。
(2)针对退役动力电池特征属性的信息增益率GR(D,Ai)计算中涉及到较多对数运算的问题,采用对数函数的麦克劳林展开式对GR(D,Ai)进行了化简,降低了算法执行时间。仿真结果表明,该方法在提高等级筛选决策树运行效率的同时对其分类结果的精确性影响较小。
(3)本文可作为后续退役动力电池重组的研究基础。
