基于生成对抗网络的小样本光伏发电短期预测

牛宇童，冯天波，李 庆，崔昊杨

(1.上海电力大学电子与信息工程学院，上海 200090；2.国网上海市电力公司信息通信公司，上海 200030；3.国网上海市电力公司闸北发电厂，上海 200432)

对于新建光伏电站而言，准确的光伏发电预测较为困难。目前较多发电量预测的深度学习方法往往依赖高质量海量数据[1]，然而新建电站气象条件相关光伏发电量样本数据积累不够，从而使预测时效性和准确率难以保证[2]。此外，在数据传输损失和噪声干扰的影响下，光伏发电量数据丢失(统计表明可达40%以上[3])或存在脏数据[3]的情况并不少见，造成可用数据样本更为匮乏。在小样本数据增强的相关研究中，肖等[4]提出基于GAN 数据生成模型和RCGAN 负荷预测模型的SLF 方法，对小样本进行样本扩充，所得结果具有良好的稳定性和准确性。Zhang 等[5]采用SolarGAN 方法补全缺失的光伏数据，误差减少至23.9%。上述研究未考虑到GAN 算法本身也需要大量的原始数据来支持网络的训练收敛，若数据量较少，容易陷入模式崩塌和梯度爆炸。此外，目前小样本光伏预测的方法由于未充分考虑气象参数的影响权重，分析不充足，输入不充分，所以依然存在一定的预测误差[6]。对此，提出基于迁移学习改进WGAN 和LSTM 的小样本光伏发电量短期预测方法。相较于文献[5]中的传统WGAN 模型，本文在此基础上引入深度迁移学习，学习已有的源域数据集知识，并迁移至对缺失样本的数据增强，生成与原始数据高度相似分布的样本；将气象参数根据与发电量的相关程度赋予不同权重作为输入，在LSTM 方法中增加了误差补偿机制，进一步降低误差。本文所提方法不仅解决了传统人工神经网络样本不足的问题，提高了生成对抗网络的泛化能力，同时有效提高了新建光伏电站小样本情况下光伏发电量预测准确率。

1 小样本数据增强与发电量预测模型构建

本文针对新建光伏电站小样本光伏发电量短期预测分别构建了数据增强模型和光伏预测模型，技术路线如图1 所示。引入深度迁移学习算法对模型微调(fine-tuning)，并以训练参数优化后的WGAN 模型对目标数据集样本进行高效扩充。在LSTM 预测中，通过对扩充数据中的气象参数与发电量作相关性和可视化分析，按照相关性程度赋予不同的权重作为输入数据，并采用相似气象条件发电值对预测结果误差进行补偿，得到最终的预测结果。

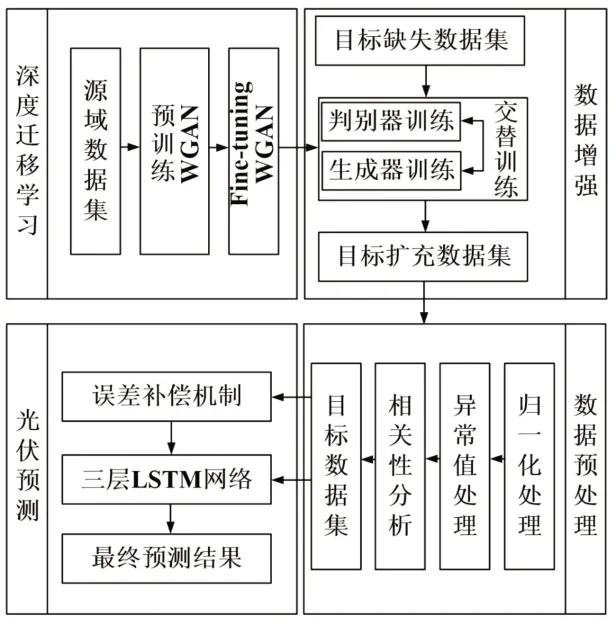
图1 小样本光伏发电量短期预测的技术路线

1.1 数据增强模型构建

常规的GAN 模型由生成网络G(generative network)和判别网络D(discriminative network)构成，如图2 所示。G 网络由LSTM 模型构成，用以生成数据；D 网络由CNN 模型构成，用以对生成数据和实际数据进行分类。同时交替训练LSTM模型和CNN 模型：G 网络学习光伏数据集的数据分布，D 网络判别光伏数据来自实际样本数据而不是生成样本数据的概率。G 网络的训练过程是最大化D 网络判别出错的概率。G 和D 的博弈存在唯一解，当D 估计概率为1/2 时，G 完成高类似光伏样本数据的生成过程。GAN 同时可反向传播训练，通过G 和D 的博弈即可完成对抗训练过程。常规GAN 的目标函数如下[7]：

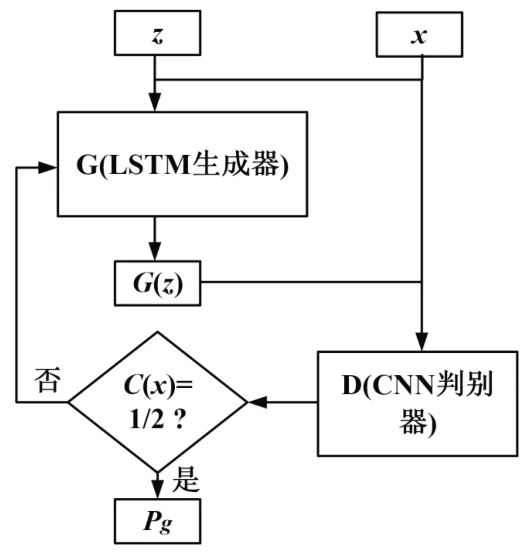
图2 WGAN 结构

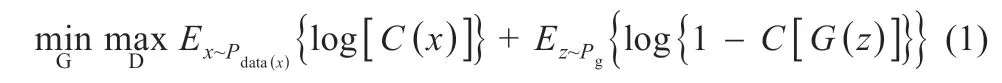
式中：Pdata为实际目标缺失数据集的样本分布。

设输入G 的天气变量和光伏参数为z～Pz，G 网络生成样本G(z)的分布为Pg，D 网络判别概率为C(x)。训练D 以更准确地判别生成样本和实际样本，同时训练G 以最小化C[G(z)]。常规GAN 使用JS 散度来衡量Pdata和Pg两个概率分布的相似度，由于Pdata和Pg几乎不重叠，无论两者差异大小，JS 散度均为常数log2，并导致生成网络梯度消失[8]。为解决该问题，利用Wasserstein 距离代替JS 散度对概率分布进行量化[9]：

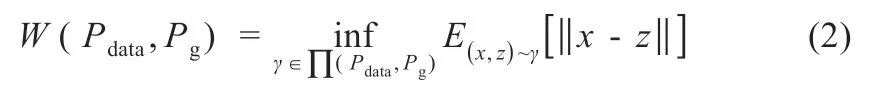
式中：∏(Pdata,Pg)为生成/实际光伏数据的联合分布。对于任意联合分布γ，取其中实际目标数据集光伏数据x和生成样本数据z，计算出两类样本距离||x－z||，得到该联合分布γ 下样本的期望值，在所有可能的联合分布中对该期望值取下限值。WGAN 的整体结构和训练过程与常规GAN 一致。WGAN 整体训练的目标函数为[5]：

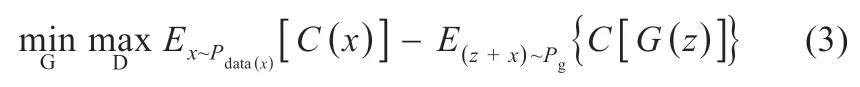
对于式(3)，将随机噪声和实际目标数据集的样本即(z+x)同作为G 网络的输入。D 网络应满足1-Lipschitz 函数集的限制条件：

鉴于原始数据集样本量不足难以训练WGAN，使用预训练的网络来重新微调，迁移学习的流程如图3 所示。先用源域数据集对WGAN 预训练，得到初始化网络参数，冻结训练参数并对模型进行层迁移，保留除全连接层外的模型参数和权重；使用少量目标域数据训练完整的新全连接层并对权重进行保存；采用层冻结的方法对部分关键层或整个模型的训练参数进行微调。训练完成后，迁移部分的权重参数对模型起到了优化效果，使得生成样本更加接近实际样本的分布。因此，将源域数据集内学到的知识用于指导生成网络的迭代优化，完成源域内知识到目标域的迁移。

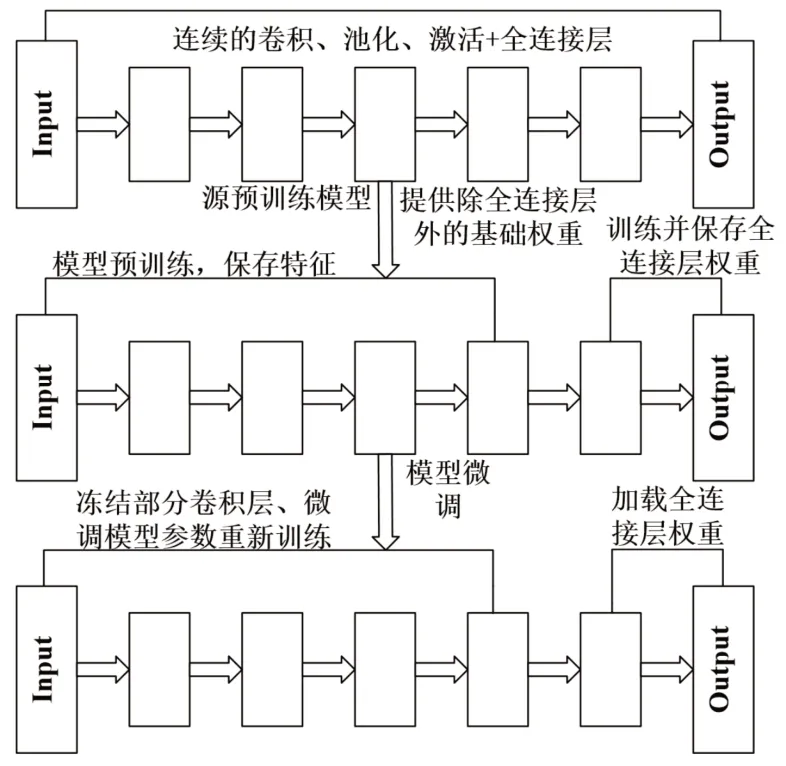
图3 迁移学习流程

1.2 光伏预测模型构建

利用三层LSTM 对扩充的目标数据集进行预测。在三层LSTM 层中，第一层结构为32×20，32 是网络输入样本数，20是样本数据纬度。第二层为32×16，第三层为32×12，输入层为1×32，输出层为1×1。使用Relu 函数作为激活函数，采用Adam 算法对各层权值进行优化，设置Dropout 机制来避免过拟合。以此，LSTM 对时序数据进行建模，并且克服了RNN中的“梯度消失”和“梯度爆炸”问题，从而实现光伏序列数据预测[10]。

为减小气象因素误差，本文增加误差修正环节。选取目标数据集中的现场温度、光照强度等气象数据构造特征向量，建立目标函数如下[11]：

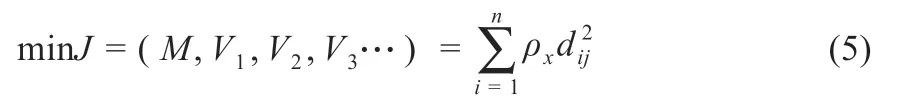
目标函数需满足以下条件：

式中：M为气象数据集；V1，V2，V3…分别为温度、光照强度等光伏气象数据；ρx为相关系数，且ρ1+ρ2+ρ3+…=1；dij为各样本点到V1，V2，V3…等光伏气象数据的欧氏距离；为滤除气象数据奇点数据和偶发因素，设定J*为最大可允许修正量，超出此范围则修正无效。

在小样本气象数据库中，搜索并比较与预测发电量值对应的气象数据最相似的样本，索引该组气象数据对应的光伏发电量实际值Pc和预测值Pr，取Pc和Pr差值的绝对值对LSTM 的初步发电量预测值进行误差补偿，获得最终发电量预测值，并将最终预测值实时上传数据库，以便进行下一次误差补偿时更加精确。计算公式如下[11]：

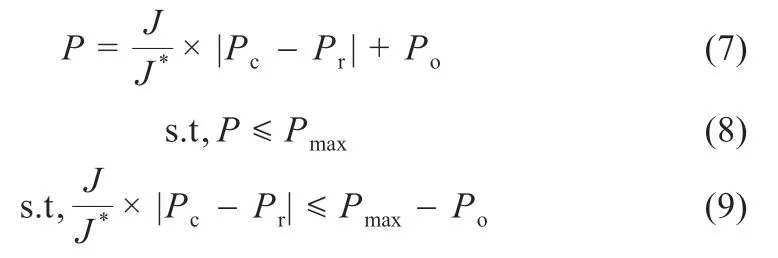
式中：Po为LSTM 神经网络的初步发电量预测值。对分子取绝对值做限幅，意味着整体预测可能偏高。由于目标数据集中发电量最高值Pmax在10～12 之间，对于计算出高于Pmax的数值，直接取预测值进行截断。

2 案例分析

实验在CUDA8.0，Tesnoeflow1.4，Nvidia Titan1080ti GPU(12G)平台下进行，以GEFCom2014 年太阳轨道的公开太阳数据集[12]为源域数据集，以2018 年DataFoutain 公开的光伏电站数据集作为目标数据集进行案例研究。使用均方误差(MSE)、均方根误差(RMSE)和归一化均方根误差(NRMSE)作为评价指标对模型精度进行评估。

2.1 数据增强结果

为评估无监督模型生成结果，设计了基于完整数据集生成小样本数据集实验。以DataFoutain 的光伏电站数据集为基础，按照40%缺失率随机删除，生成目标缺失小样本数据集；用数据增强模型补全缺失的40%数据，将生成的数据与实际数据进行比较。使用下式随机删除光伏电站数据集中的部分数据[5]：

式中：enj为光伏电站数据集中第j个样本的向量表示；Mmj为光伏电站数据集中第j个样本的0-1 矩阵，作内积处理。0 为缺失，1 则保留，从而生成40%缺失率的目标缺失数据集。使用式(2)～(4)构造WGAN 模型，训练判别网络时选择优化函数RMSProp。同时，训练生成网络和判别网络时选择优化函数为Adam，对模型的参数进行更新[13]。设置Epoch 为30，Batchsize 为16。由于太阳数据集和光伏电站数据集并不完全相同，对其作领域自适应优化。对两个数据集的数据进行二分类，尽可能筛选出太阳数据集中与光伏电站数据集特征分布相近的数据，因此，将基于太阳数据集特征训练的判别网络用于光伏电站数据集。对二分类时的损失函数进行优化来提高分类准确性，优化目标为[9]：

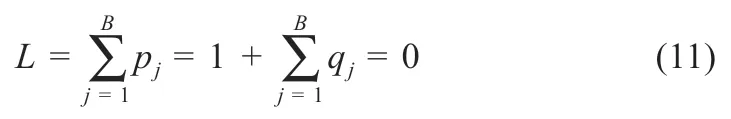
式中：pj=0 表示太阳数据集的数据标签；qj=1 表示光伏电站数据集的标签。得到分类后的太阳数据集后，利用前文的迁移学习流程对光伏电站数据集进行数据增强，得到目标扩充数据集。通过与原始目标数据集进行比较，可得扩充样本和实际样本的MSE为0.079，NRMSE为0.503。而以同样本数据库测试表明，SolarGAN 和GAN-Z 等常规模型的MSE分别为0.196 和0.369，因此本文方法生成的数据更符合实际数据分布。

2.2 数据预处理和可视化分析

对输入数据进行有效预处理可减少训练和计算代价并提高模型预测精度。本文对扩充后的光伏电站数据集进行了标准化处理，所有数据都在0～1 的特定范围内重新缩放。扩充数据集每周期每天200 个ID，则45 d 训练集数据量为9 000 条。对45 d 内的气象和电压电流等参数作散点图，图4(a)、(b)分别为平均功率和电压的特征散点图。发现平均功率和电压等各特征参数基本都存在明显异常值。根据统计学知识，异常值判定遵循以下基本规则：data∈[均值－3×标准差，均值+3×标准差]，凡是不在此范围内的数据均作奇点数据进行删除处理，并用上一点有效值替代。

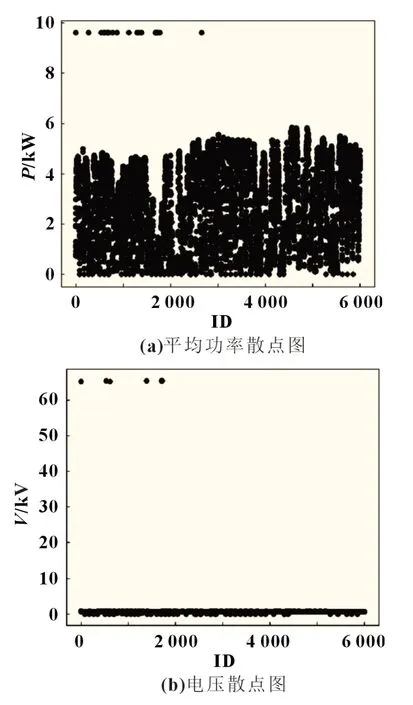
图4 目标数据集部分特征散点图

为探明各特征参数变化对光伏发电量的影响，本文计算了各气象和电压电流等参数与发电量的Pearson 相关系数，公式如下[14]：

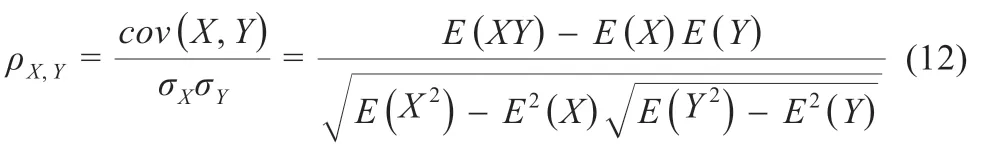
式中：X为各特征参数值；Y为光伏发电量值；总体相关系数ρ为X、Y之间的协方差和标准差乘积的比值。若其值越接近＋1 则相关性越密切，其值大于等于0.8 时，视为高度相关。各特征参数与发电量的Pearson 系数如表1 所示，根据相关性系数的大小对各特征参数赋予不同的权重。

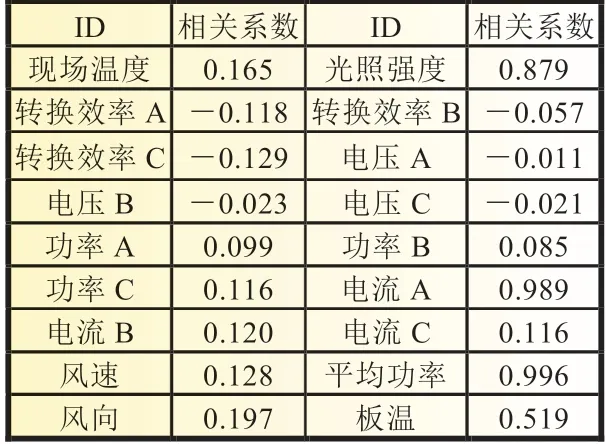
表1 Pearson 系数结果

为使相关性直观体现，本文对部分特征参数与发电量之间的变化关系数据进行了可视化处理。从图5 中发现，图5(a)、(b)分别为光照强度/40 和平均功率/480 的曲线，(a)、(b)中特征参数的变化曲线和发电量基本重合，光照强度和平均功率的Pearson 系数值也超过了0.8，所以其与发电量表现出较强相关性。图5(c)为板温的曲线，板温的变化曲线与发电量只有小部分重合，Pearson 系数值为0.519，表现出中等强度相关性。图5(d)为风速曲线，(d)中特征参数的变化曲线和发电量的重合较少，Pearson 系数值也只有0.128，表现出较弱相关性。综合分析Pearson 系数值和可视化图可以发现，与发电量具有较强相关性的为光照强度、电流A 和平均功率，具有中等强度相关性的为板温，具有较弱相关性的为现场温度、转换效率A、转换效率C、功率C、电流B、电流C、风速和风向，其余特征参数不具有相关性，可忽略不计。

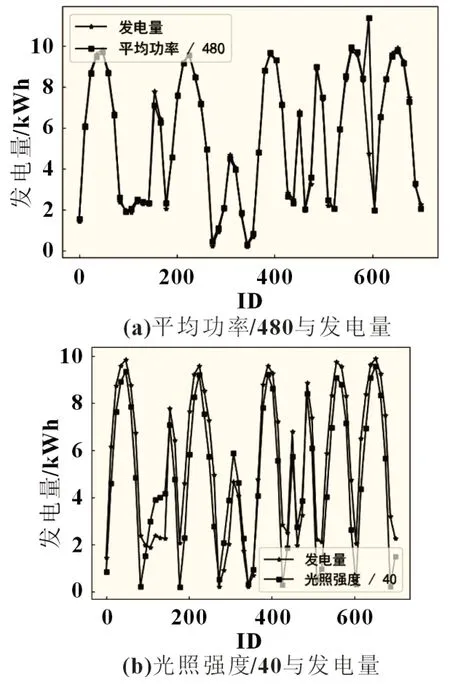
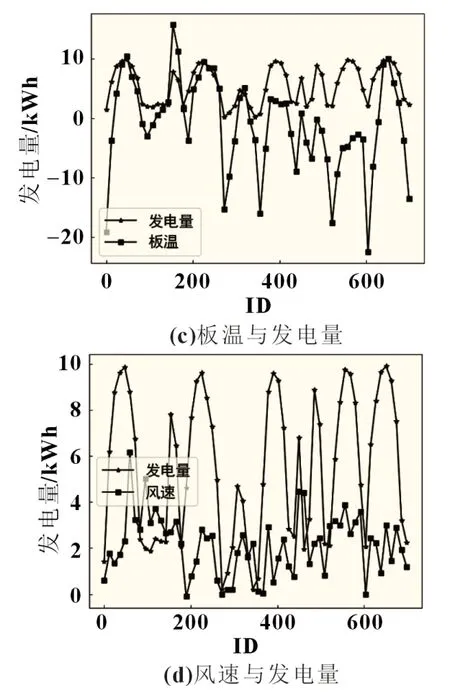
图5 部分特征参数与发电量的相关性曲线图

2.3 光伏短期预测结果及分析

通过对不同权重比时的模型预测结果的RMSE作比较，如表2 所示，可以看到，0.8∶0.1 时模型误差最小。所以赋予特征参数最优权重：光照强度、电流A、平均功率和板温权重为0.8，其他弱相关性变量权重为0.1，此时，预测值与实际值更为符合。将所有特征参数赋予对应的权重作为预测模型的输入，得到光伏电站数据集的光伏发电量预测。发现初步预测结果仍有一定误差，利用前文误差补偿方法，对结果进行误差补偿修正。修正前后的结果对比如图6 所示。由于式(7)～(9)和历史实际发电值对初步预测结果的修正作用，使得修正发电量后的预测结果比未经修正的结果误差降低了37.2%。

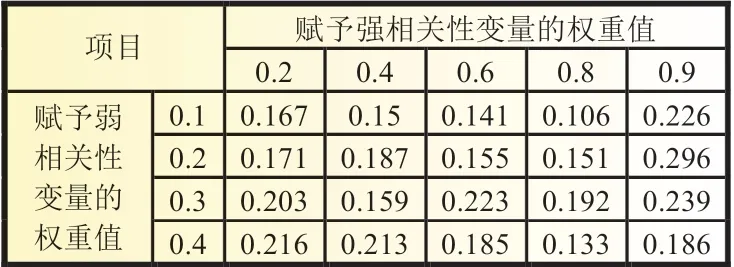
表2 不同权重比时的模型RMSE 结果

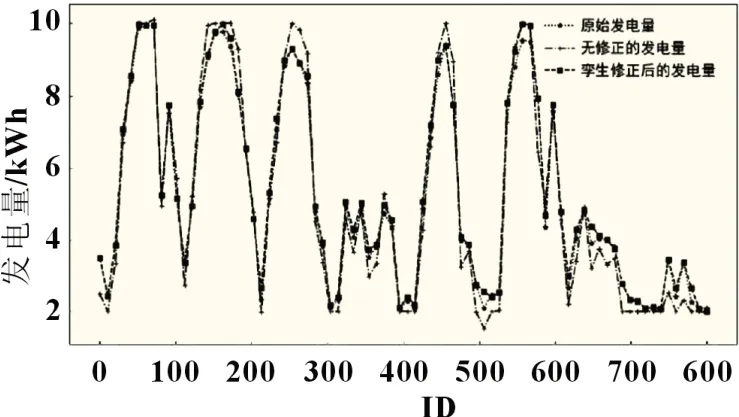
图6 误差修正结果对比

为进一步验证本文方法的有效性，将本文预测结果与常规LSTM 方法和GA-BP 方法进行比较(图7)，可以看出，在多峰值处本文方法所得结果更符合原始发电曲线。而通过比较本文方法和LSTM 模型、GA-BP 模型几个方法的发电量误差，可以看出，LSTM 模型、GA-BP 模型误差波动性较强，在－4～2之间波动，误差较大，而本文方法的误差稳定在－1～1之间(图8)，本文方法的误差相比常规方法至少降低了33.4%。

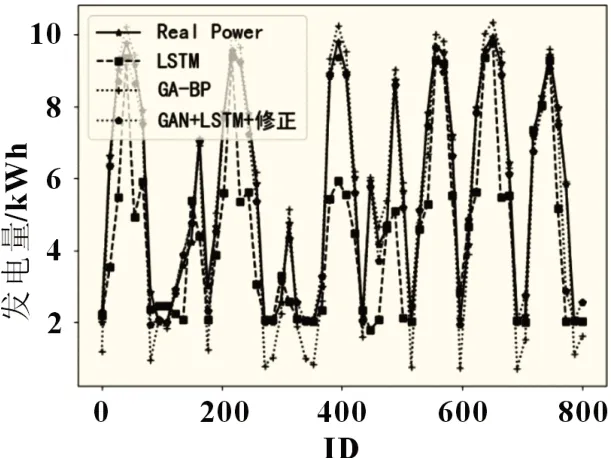
图7 光伏预测方法结果对比

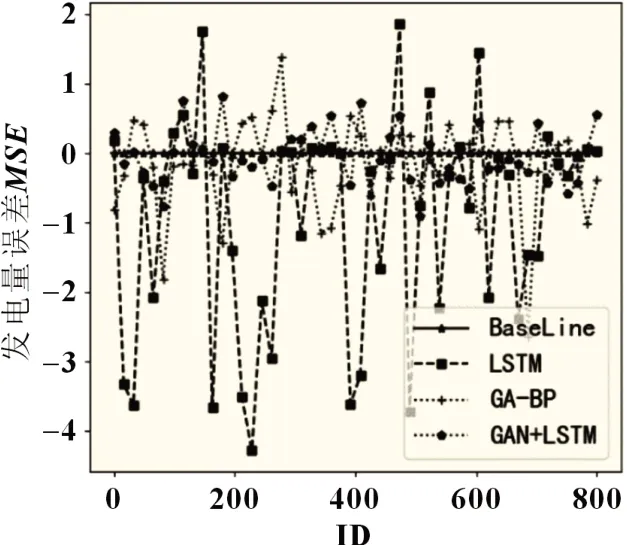
图8 光伏预测方法误差对比

3 结论

与其它未与GAN 数据增强相结合的常规人工神经网络方法相比，本文结合太阳数据集对光伏电站小样本数据集进行数据扩充，通过迁移学习方法优化WGAN 网络的初始参数设置，在有效扩充新建光伏电站小样本量的同时保证了生成样本的质量，提高了生成对抗网络的泛化能力；充分考虑气象多元参数作为输入，并根据相关性大小赋予不同权重，发电预测误差降低了33.4%。然而，对气象参数赋予的权重比只适用于光伏场景，其他新能源场景需要根据相关性另作分析；基于GAN 的网络的训练阶段比较耗时，需要减少训练阶段的计算时间，满足实时处理的需要。