基于热电耦合模型的光伏组件功率模拟
2022-11-26苏中元
彭 硕,苏中元
(东南大学能源与环境学院,江苏南京 210096)
光伏电池是一种光电转换器件,可以直接将太阳能转换为电能,它是光伏组件的核心。在实际光电转换的过程中,光伏组件的输出功率也会受到工作温度等其它因素的影响[1-2],因此准确模拟光伏组件热电性能,进而分析其实际输出性能是很有必要的。
针对光伏组件实际输出性能的模拟已经有了很多研究,一方面目前最常见的是等效电路模型[3-4],但该类电学模型对于光伏电池的工作温度只是采用简单的计算公式,精确度不高,并且常用的五参数的模型在低辐照度和高温下存在输出精度较差的问题[5],同时在模拟过程中没有将热学与电学特性联系起来;另一方面随着人工智能算法的发展,一些学者使用神经网络算法对实际光伏组件输出功率进行预测[6-7],但这种方法需要大量光伏电站的历史数据,成本较高,不方便进行工程应用。
在本研究中,提出一个热电耦合模型来对光伏实时功率进行模拟。文中构造基于等效热阻非稳态热学模型来估算太阳电池的温度,并使用七参数的双二极管模型来确保在低辐照强度下组件输出的准确性,将电学模型和热学模型耦合在一起来分析在任意工况下光伏组件性能,并根据天气实时测量数据来实现对光伏功率的模拟计算,评估光伏组件在非标准工况下实际输出性能。
1 电热模型
1.1 电学模型
1.1.1 数学模型
光伏电池双二极管电学模型如图1 所示,电路中包含一个电流源、两个二极管、一个串联电阻和一个并联电阻。
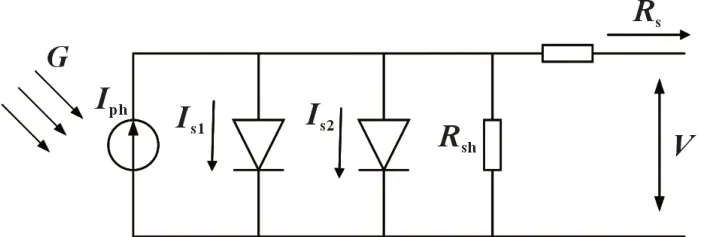
图1 光伏电池双二极管模型等效电路图
光伏电池输出电流电压关系式:
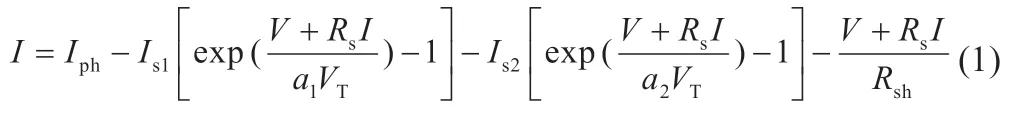
式中:V、I分别为光伏电池的输出电压和电流;Iph为光伏电池光生电流;Is1、Is2为电池二极管反向饱和电流;Rs为串联电阻;Rsh为并联电阻;VT=KTc/q,VT为二极管热电压;a1、a2为二极管品质因子;q为电子电量,取1.602×10-19C;K为玻尔兹曼常数,1.381×10-23J/K;Tc为太阳电池温度。
光伏电池双二极管模型所表示的等式是一个包含七个未知参数的超越方程,根据生产商提供的太阳电池在标准测试参数下的基本参数(开路电压Voc、短路电流Isc、最大功率点电压Vm、最大功率点电流Im),利用文献中相关的解析关系和数值迭代的方法来提取在标准测试工况下的七个未知电学参数[3]。在标准条件下参数一旦确定,就可以建立在任意工况下光伏组件关系式。
1.1.2 任意工况下参数计算
光伏电池的输出特性受到辐射强度和组件温度的影响,等效电路参数在任意工况下与辐射强度和组件温度关系计算公式[3]如下:
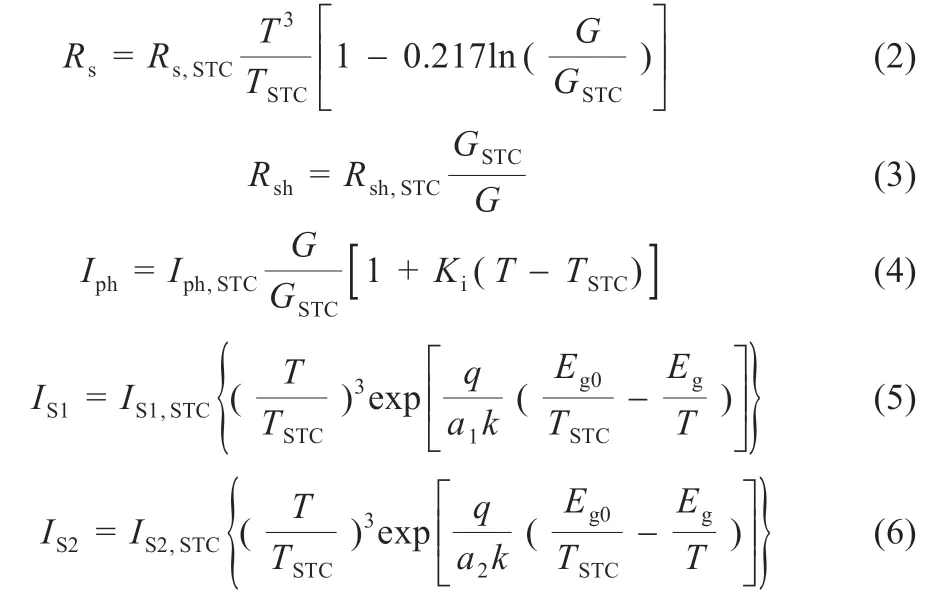
式中:G为辐照强度,下标STC 表示标准测试工况;GSTC为标准测试工况下辐照强度,取1 000 W/m2;TSTC为标准测试工况下电池温度,取297 K;Ki为短路电流温度系数;Eg0为标准工况下材料的能带间隙;Eg为材料的能带间隙。
基于上述公式便可通过绘制I-V 曲线求解出最大功率点。通常辐照强度可通过实验场的辐照仪测量得到,光伏电池温度不方便直接测量获取,而利用标称工作温度计算方法精度不高;为保证计算的精度和速度,对组件整体结构进行分析,基于等效热阻的方法,构建热学模型来估算组件的工作温度,用于光伏组件电学模型的耦合。
1.2 热学模型
单面光伏组件整体材料结构由五层组成,从表面到背面分别为:玻璃、乙烯-醋酸乙烯共聚物(EVA)、光伏电池、EVA和背板。光伏组件的能量传递如图2 所示,组件存在三种不同的热量传递方式:导热、对流和辐射,光伏组件的顶部和背部热量通过对流换热和辐射换热来耗散,光伏组件内部只存在导热。为了简化能量传递过程,对于光伏组件做出以下假设:
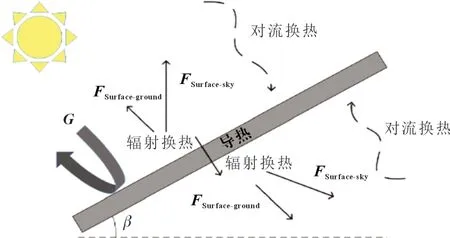
图2 光伏组件能量传递图
(1)组件各层材料各向同性,组件各层以层压的工艺结合在一起,忽略接触热阻。
(2)不考虑组件部分与边框的换热,热量传递只发生在每一层的上下两层,每层温度均匀分布。
(3)仅玻璃层和光伏电池层有热量产生,光伏组件输出功率始终为最大功率。
1.2.1 等效热阻计算
在光伏组件能量分析过程中,等效热阻是一个重要参数,它主要分为三种类型:辐射换热热阻、对流换热热阻和导热热阻。太阳能光伏组件的等效热阻网络如图3 所示。
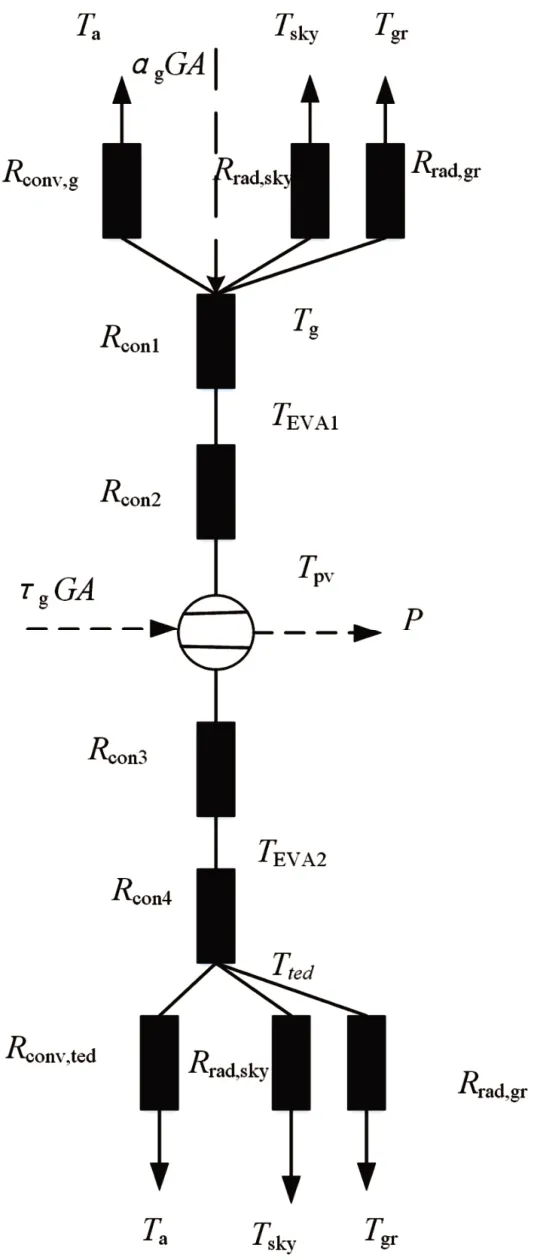
图3 光伏组件等效热阻网络图
对于辐射换热热阻,存在于光伏组件的玻璃层和背板层,它代表表层与天空和地面的辐射换热损失,等效辐射换热热阻计算公式为:
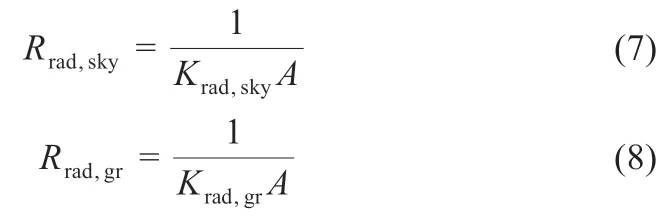
式中:A为面积;Krad,sky为表面与天空的辐射换热系数;Krad,gr为表面与地面的辐射换热系数;Rrad,sky为与天空的辐射换热热阻;Rrad,gr为与地面的辐射换热热阻。
光伏组件安装在室外环境,其上下表面与环境进行对流换热,组件的对流等效热阻计算公式为:
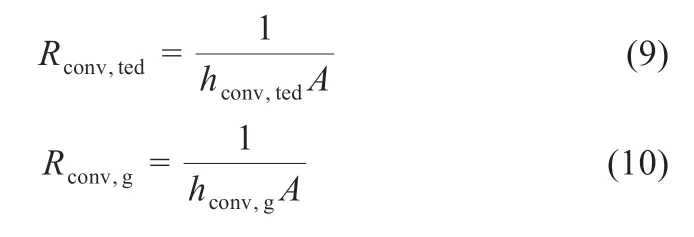
式中:hconv,g、hconv,ted为玻璃和背板的对流换热系数;Rconv,g为玻璃与环境的对流换热热阻;Rconv,ted为背板与环境的对流换热热阻。
上下表面的对流换热系数采用经验公式进行计算[8]:
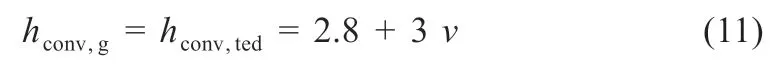
式中:v为风速。
组件内部的能量以导热的形式传递,导热热阻计算公式为:
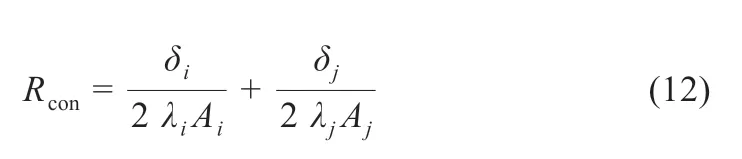
式中:下标i、j代表光伏组件不同层;δ 为厚度;λ 为热导率;Rcon为不同层的等效导热热阻。
1.2.2 能量守恒等式
基于光伏组件的等效热阻网络,在非稳态状况下各层的能量守恒等式如下:
(1)玻璃层:
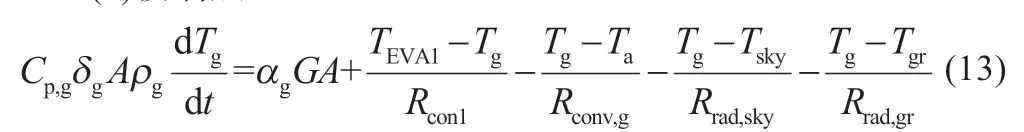
(2)上层EVA 层:
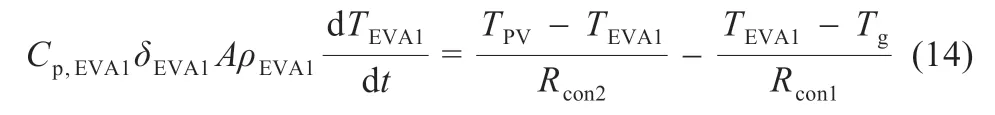
(3)光伏电池层:
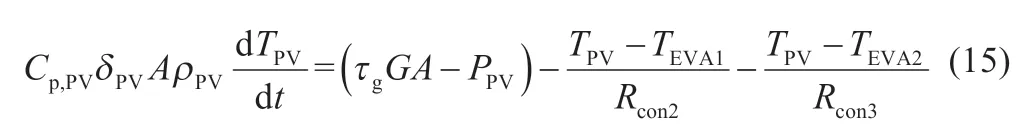
(4)下层EVA 层:
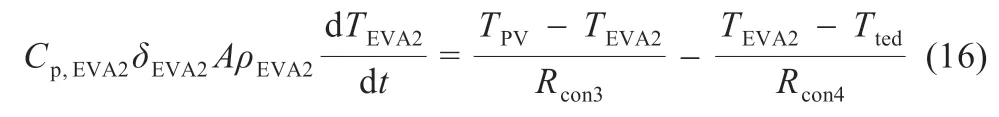
(5)背板层:

式中:Cp为材料比热容;ρ 为材料密度;δ 为材料厚度;α 为材料吸收率;τ 为材料透射率;T为材料层温度;下标g、EVA1、EVA2、PV、ted 分别代表玻璃、上层EVA、下层EVA、光伏电池、背板材料;Ta为环境温度;Tgr为地面温度;Tsky为天空温度。
2 耦合模型求解
提出的电学模型和热学模型可以耦合在一起用于模拟计算光伏组件的输出功率。整体耦合方式如图4 所示,基于等效热阻的热学模型用于计算光伏电池工作温度,代入到双二极管电学模型,电学模型模拟的输出功率又作为热学模型的内热源,通过这一耦合机制最终模拟输出光伏组件功率。
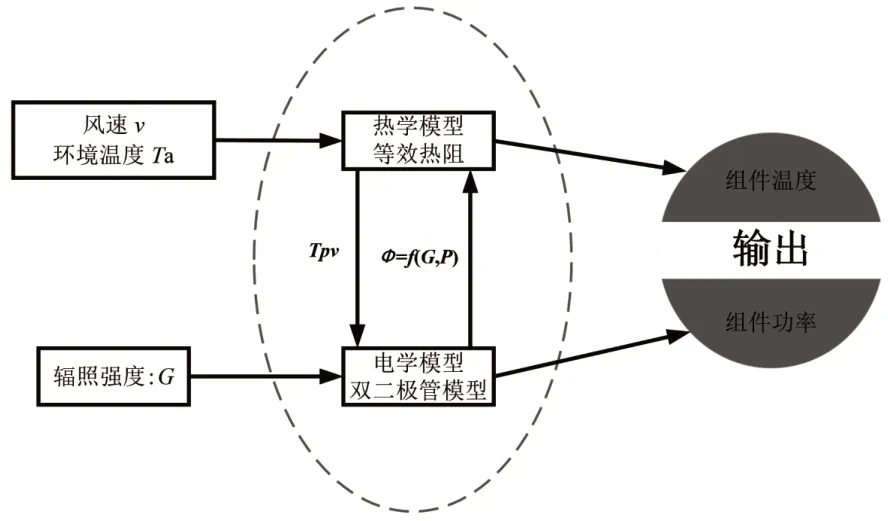
图4 模型耦合示意图
具体计算流程如图5 所示。首先通过制造商提供的光伏组件基本参数提取标准状况下初始参数,然后把一系列参数包括:辐照强度、环境温度、风速、光伏组件物性参数和初始面板参数代入热电耦合模型中,光伏电池的温度可以通过构造的热学模型迭代计算得出,通过耦合计算,就可以对光伏组件的功率进行模拟计算分析。
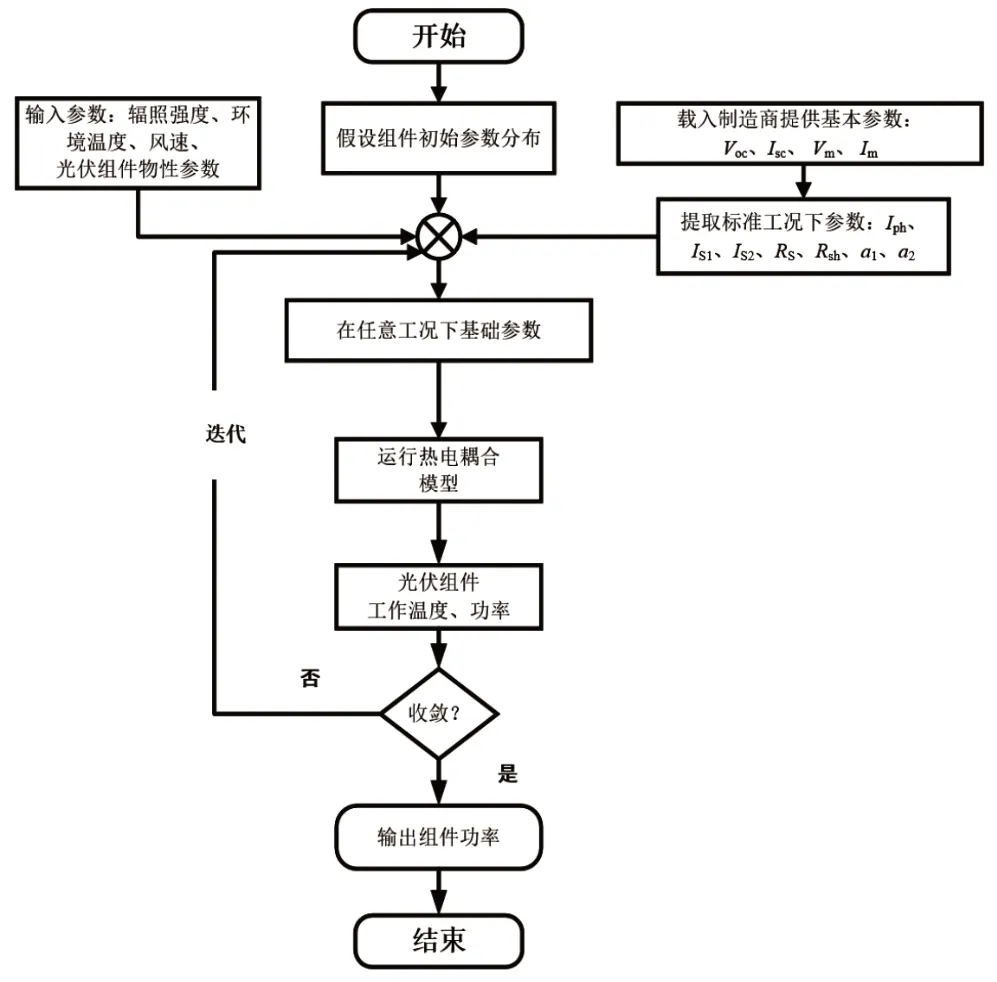
图5 求解流程图
3 结果与讨论
3.1 电学模型验证
为了验证本文所提出使用的电学模型,使用文献中所提供的相关数据[9],通过模型计算绘制光伏组件的I-V 曲线并与实际测量值进行对比验证。验证结果如图6~7 所示,图6 展示了MSX60 光伏组件在环境温度25 ℃,太阳辐射强度从400~1 000 W/m2情况下的特性曲线;图7 显示在1 000 W/m2辐照强度下,温度从25~75 ℃的特性曲线变化情况。经验证所使用电学模型模拟曲线与实验数据很好地吻合。在三个特征点没有明显的差异(短路电流点、开路电压点和最大功率点),在最大功率处相对平均误差为1.3%,可以准确反映光伏组件的输出特性。
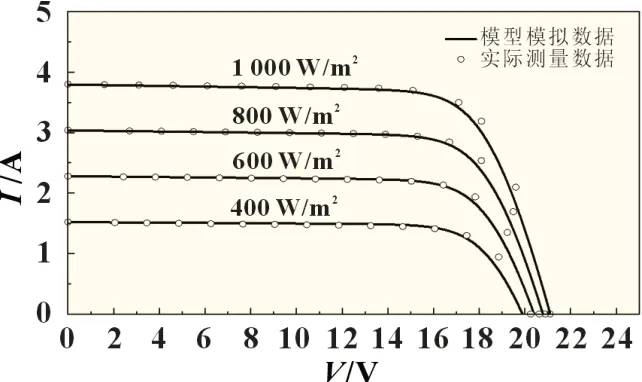
图6 辐照强度对特性曲线影响
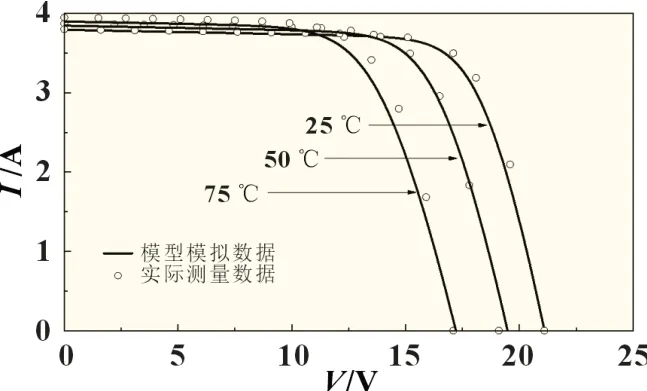
图7 温度对特性曲线影响
3.2 热学模型验证
热学模型是热电耦合模型的一个重要组成部分,它估算出光伏模块的工作温度可以作为电学模型的一个输入参数。为了验证所提出热学模型的准确性,将模拟结果与实际测量结果进行比较,选用210 mm 单面光伏组件为实验测量对象,光伏组件实际温度数据采用红外摄像仪在一天特定间隔测量收集。而且本文提出的热学模型还与工程中常用的NOCT模型和Sandia 模型[10]进行比较验证。本文所用实验组件材料参数如表1 所示。
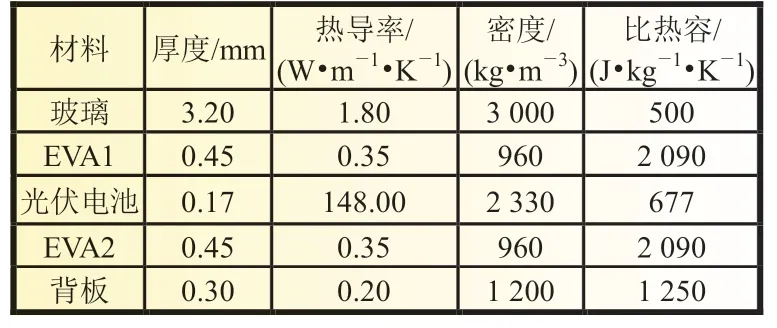
表1 光伏组件的参数表
验证结果如图8 所示,我们可以看出光伏电池温度受环境温度和太阳辐射的影响。为了评估这些热学模型,采用温度的相对误差这一参数。比较可以发现本文提出的热学模型比NOCT 模型和Sandia 模型更准确,最大温度误差1.9 K。本文热学模型相对平均误差仅为3.8%,而NOCT 模型和Sandia 模型相对平均误差分别为16.2%和32.3%,因此本文提出的热学模型在整体上可与实际测量值贴合,可用于估算光伏电池工作温度,与电学模型耦合来模拟光伏组件的输出功率。
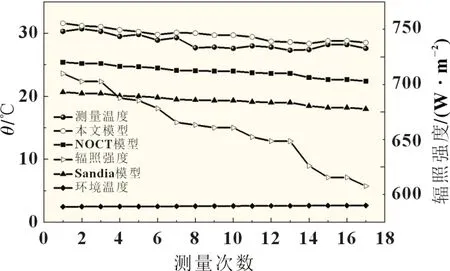
图8 不同热学模型计算结果比较
3.3 耦合热电模型验证
室外环境下光伏组件的输出功率随着天气情况不断变化,在不同天气状况下获得其输出功率是很有必要的。因此为了更好地评估耦合模型的可靠性,选用一年中三个典型的天气(晴天、阴天、多云)的测量数据用于模拟验证。
本文提出模型计算结果与实验数据很好地吻合,通过分析,测量的实验数据显示光伏组件输出功率随着辐照度不断变化。从图9~11 显示结果来看,在三种不同天气下,晴朗天气的光伏组件输出要优于其余两个天气。在晴朗天气不存在云层的遮挡而且有更好的太阳辐射,所以模拟计算结果与实验数据很好地吻合。模型最低均方根误差为7.1%。但在其余两种天气情况,由于太阳辐射强度的变化和云层覆盖遮挡问题,提出的模型与实验数据存在一定偏差。
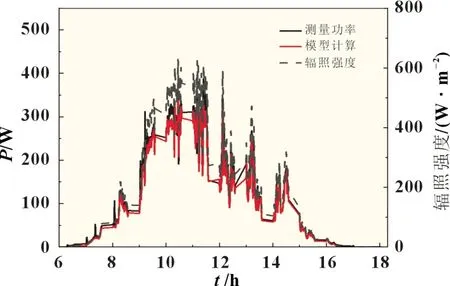
图9 多云天气下光伏组件模拟值和实测值对比
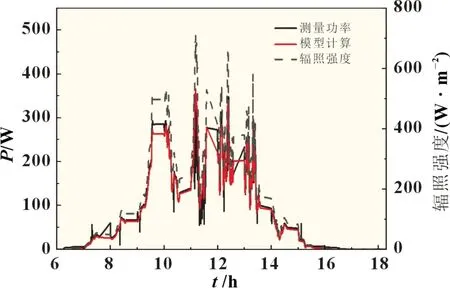
图10 阴雨天气下光伏组件模拟值和实测值对比

图11 晴天天气下光伏组件模拟值和实测值对比
文中提出的模型和实验数据存在细微差别,主要由以下原因导致:一方面,当太阳角度发生改变,光伏组件存在被遮挡的情况,将导致输出功率减少,在提出的模型动态计算过程中,这一因素并没有被考虑进去;另一方面,传感器和数据收集器之间存在时间延迟,这会导致在实验数据收集中存在时间误差。
4 结论
本文展现了光伏组件热学与电学性能的耦合模型。这个热电耦合模型用于模拟在三种不同天气下光伏组件的热学和电学性能,可以基于实时天气数据对光伏组件功率进行快速计算。研究中得出结论如下:
(1)采用的双二极管模型适用于电学模型,在三个特征点没有明显的差异,在最大功率点相对平均误差1.3%。
(2)综合考虑组件的结构差异和辐射换热因素,构建的基于等效热阻的热学模型模拟的光伏电池温度在整体上与实际测量值吻合。与NOCT 模型和Sandia 模型相比,该模型有更低的相对平均误差(3.8%),适用于耦合模型。
(3)通过对三种典型天气下热电耦合模型模拟值与实测值进行对比验证,模拟结果在不同天气下与实验结果很好地吻合。与其余两种天气情况相比,晴天有更好的表现和更高的精度,最低的均方根误差为7.1%。该热电耦合模型可对光伏组件输出功率进行快速计算,有着较高的精度和适用性。
