利用“蝴蝶法”求解一次函数自变量取值范围
2022-11-25甘肃省武威市凉州区谢河镇九年制学校他维武
⦿甘肃省武威市凉州区谢河镇九年制学校 他维武
无论是在单纯的函数问题,还是应用题中,一次函数中自变量的取值范围始终是重要内容,同时也是学生难以突破的一个考点[1].基于此,本文中首先介绍平面直角坐标系中一条直线对应的函数的自变量取值范围,然后拓展到两条相交直线中利用“蝴蝶法”讨论自变量的取值范围,希望在帮助教师教学的同时也能帮助学生突破难点.
1 引例分析
例1已知函数y=2x-4,要使y>0,那么x的取值范围是______.
分析:这是一道一次函数与不等式结合的题目,比较常见且难度不大,有两种不同的解法.解法一,由y>0得到2x-4>0,解出不等式后即得x的取值范围.解法二,画出函数y=2x-4的图象,借助图象分析出x的取值范围.
解:用两点法作出函数y=2x-4的图象,如图1所示.
图1中,x=2时,y=0.直线y=2x-4被点(2,0)分成上下两部分.如图2所示,在直线上半部分中取若干各点,分别找出这些点对应的横、纵坐标,发现x大于2时,y都大于0,于是有“x>2时,y>0”.
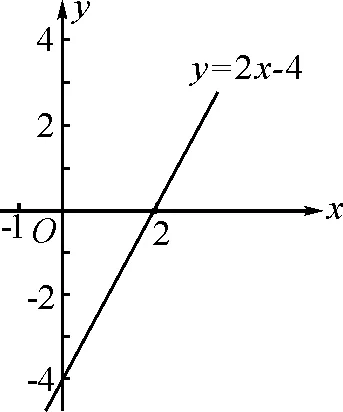
图1
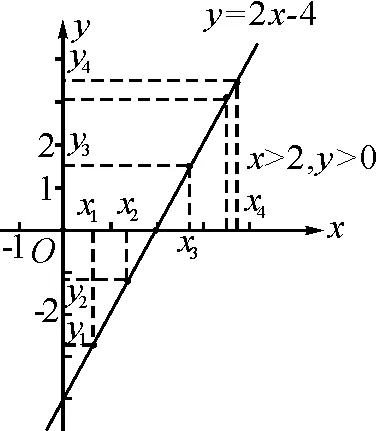
图2
接下来,在直线下半部分中取若干个点,分别找出这些点对应的横、纵坐标,发现x小于2时,y都小于0,于是有“x<2时,y<0”.
所以,y>0时x的取值范围是x>2.
点评:通过函数图象分析自变量的取值范围大致分为以下几个步骤.(1)找图象与x轴的交点,确定y=0;(2)将直线分为上下两部分,取若干点讨论x,y;(3)比较大小.当然,还可以通过观察图象直接得到直线上半部分中的点相应的y值都大于0,直线下半部分直线中的点相应的y值都小于0,即“上大下小”[2].
2 例析“蝴蝶法”
所谓“蝴蝶法”,是根据同一坐标系中两条直线形成的图形而产生的方法,其基础是例1中的方法,只不过是将一条直线换成了两条直线.下面通过例2说明如何用“蝴蝶法”解决一次函数自变量的取值范围.
例2已知函数y1=x-1和y2=2x-3,当y1>y2时,x的取值范围是______.
分析:本题可采用两种方法解答.法1可以直接根据y1>y2得到不等式x-1>2x-3,解之即可得到x的取值范围.法2采用图象法,即先画出函数图象,然后根据“蝴蝶法”分析.
解:首先,画出两函数图象,如图3所示.
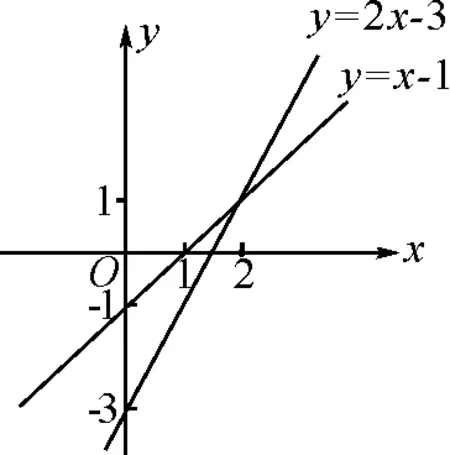
图3
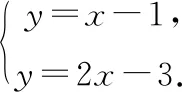
即当x=2时,y1=y2.
再次,找“蝴蝶”.两条直线将整个平面直角坐标系分成了四部分,利用“引垂法”找到垂线与两直线的交点,交点所在直线之间部分(如图4所示)即为所找“蝴蝶”.
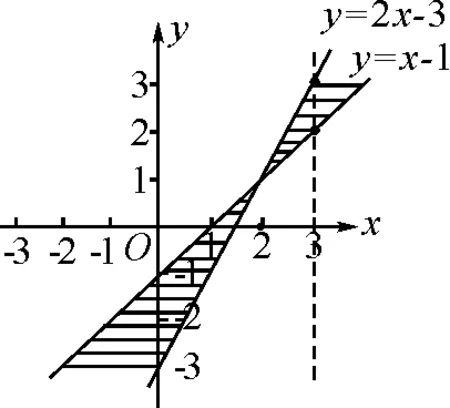
图4
最后,由图可以发现y1>y2部分主要在交点左边部分“蝴蝶”,而这部分的横坐标全部小于2.于是,得到了当x<2时,y1>y2.那么交点右边部分的“蝴蝶”的横坐标全部大于2.于是,得到了当x>2时,y1 综上,应填答案:x<2. 例3图5表示一艘轮船和一艘快艇沿着相同路线从甲港出发到乙港行驶过程中路程随时间变化的图象.根据图象解答下列问题: 图5 (1)在轮船和快艇中,哪一个的速度较大? (2)当时间x在什么范围内时,快艇在轮船的后面?当时间x在什么范围内时,快艇在轮船的前面? 分析:第(2)问是本文研究的对象,主要方法是求出两条直线交点,然后利用“引垂法”找到“蝴蝶”,再用“蝴蝶法”找到自变量的取值范围. 解:(1)在轮船快艇中,快艇的速度更大,快艇的速度为40 km/h. (2)两函数图象交点的横坐标为4.当x<4时,轮船在快艇的前面;当x>4时,快艇在轮船的前面. 点评:在运用“蝴蝶法”求自变量取值范围的过程中,用“引垂法”找准“蝴蝶”非常关键.若不掌握此法,学生极易出现选左右两个部分的错误,继而无法准确找出y1>y2或y1 用“蝴蝶法”求一次函数自变量取值范围的步骤如下: (1)画图象.根据题目需要,利用“两点法”快速画出函数图象. (2)求交点.联立一次函数解析式,解之即可求出直线交点坐标.此时,要透彻理解交点的意义.以例2中的交点坐标(2,1)为例,其意义为当x=2时,y1=y2. (3)找“蝴蝶”.为了避免找错“蝴蝶”,通常利用“引垂法”,如例2解题过程中所写. (4)比大小.这里的比大小,一方面要比较x的大小,另一方面要比较y的大小.首先,欲找到x的取值范围,只需将x与交点横坐标比较.其次,欲找到y1>y2或y1 使用“蝴蝶法”时,还需注意以下两个方面: (1)正确画出函数图象是关键,所以学生要牢固掌握“两点法”. (2)“引垂法”的关键在于找到直线上一个点后,分别作出它与x,y轴的垂线,其垂足之处对应的数字的绝对值就是该点到坐标轴的距离. “蝴蝶法”作为一次函数自变量取值范围问题的解决方法,其适用范围非常广,一次函数与二次函数图象或一次函数与反比例函数图象等都可以利用.另外,在利用该法解决问题时,教师要注重学生图象观察能力的培养,让学生在数形结合中体会数学的魅力,进而掌握这类问题的解决方法[4].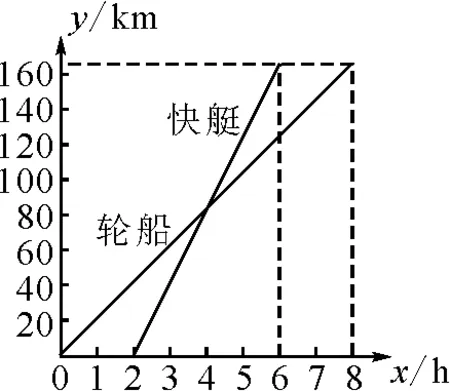
3 总结与反思
4 结语
