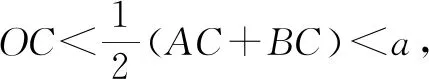基于思维能力培养的一节课堂教学评析
——从“正多边形与圆”谈起
2022-11-25江苏省泰州市姜堰区张甸初级中学王雨霞
⦿江苏省泰州市姜堰区张甸初级中学 王雨霞
在“正多边形与圆”这一章节的教学中,常常会出现这样的现象:学生能理解正多边形与圆的关系,但是在解决具体问题的时候,总是不得其法.因此大多教师就采取刷题的方式,以增加学生的解题体验,期望让他们识记更多的题目,进而提升数学成绩.事实上,这样的培养方式不利于学生的可持续发展.教师要关注学生的思维品质,要让他们具备一定的高阶思维能力,比如创新能力、推理能力等,进而能以一题应万题,既提升数学素养又减轻学业负担.
1 创设问题情境,激活数学思维
教师在教学的过程中要设置一定的问题,促使学生进入思考状态,不再游离于教师所讲述的知识点之外.教师设置的问题要在一定的情境中进行,这样才能使学生对提出的问题有更感性、更直观的认识,进而也能找寻到相应的解决方法.事实上,将问题与情境对接能让学生的多元感官参与到思考中,思维的火花也逐渐被激活.以下面的探究活动为例.
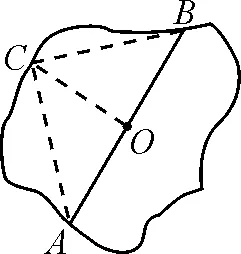
学生在小组合作讨论一团周长为4a的线圈时,发现了如下两个命题:如图1所示,当线圈做成正三角形ABC时,能被半径为a的圆形纸片完全盖住;如图2所示,当线圈做成正方形ABCD时,能被半径为a的圆形纸片完全盖住.
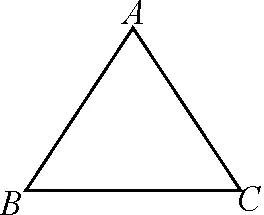
图1

图2
教师追问:对于图1、图2所展示的两个命题,能不能再想出一个命题呢?学生遇到的情境是两幅图以及图中所呈现的命题,学生要解决的问题是创设新的问题.有了情境,学生会觉得问题更容易解决.他们发现“能被半径为a的圆形纸片完全盖住”是以上两个命题共有的结论,不同的是线圈做成的图形发生了变化,由原先的三角形变成了正方形.因此,有学生就想出这样的命题:将线圈做成平行四边形ABCD时,能被半径为a的圆形纸片完全盖住.
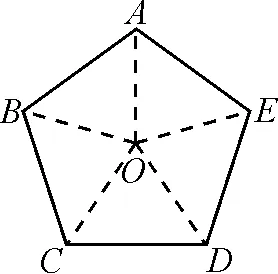
学生作出如图3所示的平行四边形ABCD,再连接AC,BD交于点O.由条件OB+OD 图3 在数学教学的过程中,教师要培养学生的思维能力,就要让学生顺着问题继续思考,以提升他们的创新能力.当前的数学教学中,学生更多的时候只是在被动地完成教师布置的题目,题目做完了,思考也就结束了.其实教师要培养学生深度学习的能力,要让学生的思维持续发展,以探究出更多的数学奥秘. 图4 要激发学生的思维就要为学生提供更多的体验机会,在体验中学生的能力会得到多方面的生长.给学生体验的机会,其实就是给他们运用所学认知解决实际问题的机会.当前的数学教学中,存在着学生解决实际问题的能力不强的现象.这主要有两个方面的原因,一是教师在教学中没能将生活中的问题引入课堂,二是学生没能主动将实际问题与课堂认知对接.因此,教学中教师要关注生活中的问题,以提升学生的数学思维. 还以图3展现的命题为例,学生提出了一个值得思考的问题:生活中见到的图形大多是任意的,如果当线圈做成任意形状的图形时,是否还能被半径为a的圆形纸片完全盖住?学生的思考已经突破了课堂所给的基本图形的范围,他们将生活中随处可见的不规则图形带入课堂,同时想发现这些不规则图形之中是否蕴含着一些规律.思维跳出原有的框架,进入新的场域. 图5 总之,在数学教学的过程中,教师要关注学生的思维生长,给他们适切的土壤,让他们开出美丽的思维之花.教师要培养学生的思维能力,真正落实数学教学的主要目标,进而促进学生的全面发展.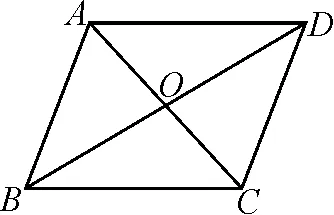
2 创新问题设计,促发数学思维
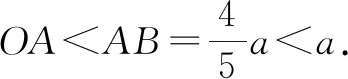
3 解决实际问题,提升数学思维