正方形对角线性质的再探究

⦿宁波科学中学 王 震

1 引言

正方形是初中数学的一个重要内容，因其具有独特的图形特点、图形风格、图形性质，也是中考的一个重要考点，特别是正方形的对角线更值得深入探究.下面就一起走进正方形对角线的探究天地，共赏正方形的美景！

2 性质探究

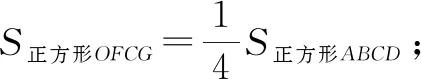
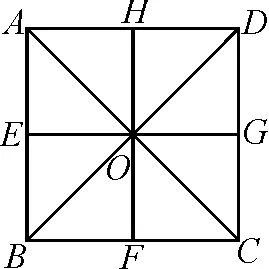
图1

下面给出性质①的几种证明，供学习时借鉴.

证法1：三角形全等法.

因为四边形ABCD是正方形，对角线AC，BD相交于点O，所以∠OCF=∠OCG=45°.

因为OG⊥CD，OF⊥BC，所以∠OFC=∠OGC=90°.又OC=OC，所以△OFC≌△OGC.即得OG=OF.

证法2：三角形面积法.

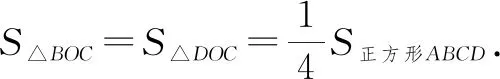
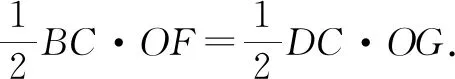
这里仅提供两种常见的证明方法，供参考.其余性质的证明读者感兴趣的，可以尝试自己完成.

3 性质应用

3.1 借助四边形的面积，求正方形的边长

例1(2021·重庆中考)如图2，正方形ABCD的对角线AC，BD交于点O，M是边AD上一点，连接OM，过点O作ON⊥OM，交CD于点N．若四边形MOND的面积是1，则AB的长为( ).

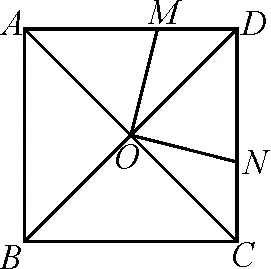
图2

解析：如图3，过点O分别作OG⊥AD，垂足为G，OH⊥CD，垂足为H.根据性质，得OG=OH.

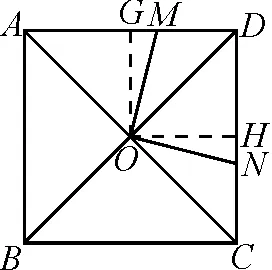
图3

∵OH⊥OG，OM⊥ON，

∴∠GOM=∠HON，

∠OGM=∠OHN.

∴△OGM≌△OHN.

故四边形GOHD的面积等于四边形MOND的面积，等于1.

由四边形ABCD是正方形，则其面积为四边形GOHD的面积的4倍，等于4，所以AB=2.

故选答案：C.

点评：根据正方形的特点，过正方形的中心引两边的垂线，利用三角形的全等，化已知四边形的面积为正方形一角四边形的面积，从而根据正方形的面积是一角四边形面积的4倍计算即可.这个结论有着重要的应用，若遇到填空题或选择题是可以直接运用，从而提高解题的效率.

3.2 构造中位线，求中位线的长

例2(2021年天津)如图4，正方形ABCD的边长为4，对角线AC，BD相交于点O，点E，F分别在BC，CD的延长线上，且CE=2，DF=1，G为EF的中点，连接OE，交CD于点H，连接GH，则GH的长为．

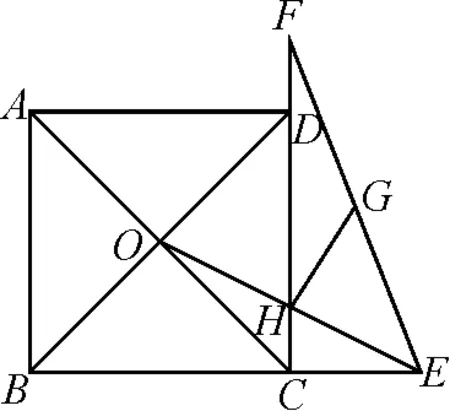
图4

解析：如图5，过点O分别作OM⊥BC，垂足为M，ON⊥CD，垂足为N，连接OF.

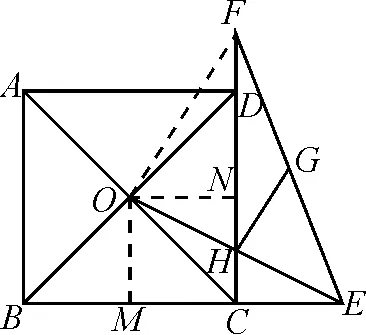
图5

在Rt△ONF中，根据勾股定理，得

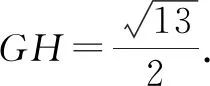
点评：解答时，把握好如下三点.(1)学会过正方形对角线交点引垂线构造顶角正方形，为性质的使用奠定基础；(2)灵活运用三角形中位线定理找中点，求线段的长度；(3)活用正方形的性质，定直角确定直角三角形，为勾股定理的使用创设解题条件.

3.3 利用性质，判断结论的正误

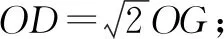
图6

A. ①②③④ B. ①③④

C. ①②③⑤ D. ①②④⑤

解析：因为正方形ABCD中，对角线AC与BD相交于点O，所以OD=OB.因为点F是DE的中点，所以OF是△DBE的中位线，即OF∥BE，并且BE=2OF.因为CE=4，OF=6，所以BE=12，BC=8.又OG是△DBC的中位线，所以OG=4，于是GF=2.故结论①正确.

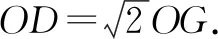
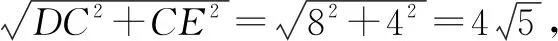
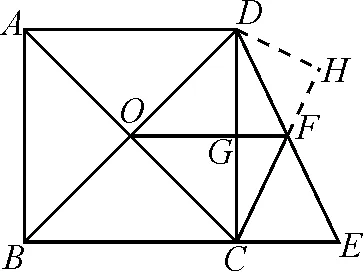
图7

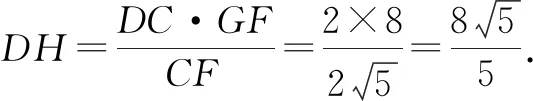
故选答案：C.

点评：解答时，要把握如下几个关键知识点.一是熟练掌握正方形的性质，特别是对角线平分对角性质；二是熟练掌握等腰直角三角形的性质；三是灵活运用直角三角形斜边上的中线性质；四是灵活运用特殊角的三角函数值，锐角的正切的性质，这也是解题的有效方法；五是熟练掌握三角形面积不同表示法，这也是一种经常用到的解题思路，特别是当思维打不开时，聚焦这个思维方向，往往会收到柳暗花明的效果，值得多重视、多运用、多关注.

4 解后反思

通过解题，得到如下启示：(1)正方形是一种特殊的四边形，其特殊性往往是解题的重要依据或是解题的重要途径，因此常态学习中，要引起高度重视，并熟练掌握和活用.(2)以正方形为背景的考题非常容易与勾股定理、直角三角形斜边上的中线、三角形的中位线定理、等腰直角三角形、图形的面积、特殊角的三角函数值有机融合，成为培养知识综合运用能力、解题能力的有效载体，更值得重视.(3)对正方形的学习要从章内综合和跨章节综合两个层面去把握.章内综合要立足正方形的性质，重点放在对角线的性质、正方形的对称性质；熟练掌握好正方形的对角线与边之间的关系，这是一个非常关键的结论型关系，往往成为解题的“桥梁”.跨章节综合立足于三角形的相似、三角函数，特别是特殊角的三角函数值问题，更是生成跨章节综合的有效生长点和重要结合部，在常态的学习过程中，要格外重视，且养成主动向这个方向拓展、延伸的好习惯，进而提升自我数学综合解题能力；正方形与勾股定理的联系也十分密切，正方形四个角是直角，对角线互相垂直、平分又生成直角，这些都为勾股定理的使用培植了知识沃土，为定理运用创造了条件.当然，正方形的跨章节综合还有旋转、平移、全等等类型，鉴于篇幅，在这里就不再赘述.