智慧引领 模型破冰
——对“圆周角(第1课时)”教学设计的思考
2022-11-25湖北省咸宁市教育科学研究院廖明芳
⦿湖北省咸宁市教育科学研究院 廖明芳
⦿湖北省咸宁实验外国语学校 许丽琴 王 弯
1 问题呈现
九年级开始学习圆周角的概念,通过与已有“圆心角”概念对比得出圆周角概念,而在圆周角定理得出的环节,人教版数学教材九年级上册第86页用了下面这段文字:
如图1,为了证明上面发现的结论(圆周角定理),在⊙O任取一个圆周角∠BAC,沿AO所在直线将圆对折,由于A的位置不同,折痕会:(1)在圆周角的一条边上;(2)在圆周角的内部;(3)在圆周角的外部.
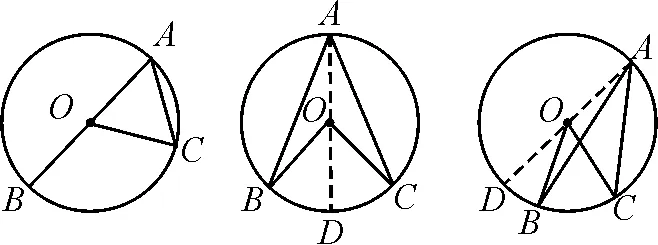
图1
2 问题诊断
根据教材呈现内容,为引出圆周角的概念,很多教师设计了“将圆形纸片动手折一折”的教学环节,这样圆周角的出现比较容易,进一步测量圆周角和同弧圆心角也不困难,于是顺理成章“猜一猜”:一条弧所对的圆周角等于它所对的圆心角的一半.到了关键“证一证”环节,问题来了:(1)教材中的这条折痕在证明过程中意义非凡,如何出现?(2)圆心角和圆周角的位置关系为何直接导致证明过程的差异,以及如何分类?
基于以上两个问题,教师用“折痕说”很难将问题自然过渡,只能采用强制引入的方式,凭空出现这条“折痕”,进而证明,使得整节课的逻辑链条断裂,干扰、打乱学生思维.
3 问题解决
经过反复实验,我们工作室的教师最终采用如下途径来解决本节课的难点.
3.1 情境导入,引出新知
播放神舟十二号发射及其与天和核心舱对接过程的短视频,抽象出圆周角,引出研究目标,同时增强学生的民族自豪感.
3.2 对比旧知,得出新知
从已知圆心角概念引出新的研究对象圆周角,二者的区别就在于顶点位置的不同,也就是角的基本要素之一(抓住几何研究对象的基本要素).而对几何对象研究的基本问题就是元素之间的位置和数量关系[1],于是引发学生探究二者之间关系的内心需求.
3.3 测量猜想,尝试总结
通过动手画角、测量、辅助计算机度量,可快速得出结论,但在此处对结论的表述,教师要潜意识进行引导,将“圆周角”放在前——圆周角等于同弧所对圆心角的一半.这个不显山露水的操作是为了给学生做出良好导向,表明要证明的核心问题是圆周角与圆心角的大小关系,是把未知的圆周角转化为学过的圆心角问题来解决.
3.4 观察探究,智慧思考
教材中直接给出了折痕与圆周角的位置关系,思维跳跃性过大.此处借助《几何画板》,让圆周角顶点在规定弧上连续移动,仔细观察此时同弧所对应的圆周角和圆心角的变化,学生易得出:圆心角是唯一的,而圆周角是无数的.对于变化的圆周角和确定的圆心角,我们如何来进行研究?(变化之中的不变性)
对几何对象的研究仍然应该从它的基本元素入手,通过圆周角顶点的位置变换,引发学生思考:圆周角和圆心角的位置关系到底能出现多少种?对变化情况进行分类,并把问题进行分割,使角度减小,让学生先观察圆心(圆心角顶点)与圆周角的位置关系.通过《几何画板》的操作能够避免“折痕说”中的局限性,使得圆周角无间断、连续变化,全面不遗漏地考虑问题.而直观变化的动态可以帮助学生找到关键的三个位置(如图2),为下一步证明做好铺垫.

图2
3.5 合理分类,模型探路
要证明圆周角定理,很自然地在上面(图2)三种位置关系中引进同弧所对的圆心角.第一种位置关系最为特殊(如图3),其他两种均涉及到作关键辅助线,也就是“折痕”的出现.
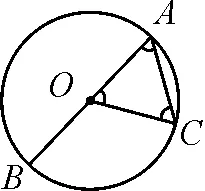
图3
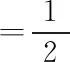
由易到难,第一种位置关系的证明学生很快可以得出.证明过程中用到了等腰三角形顶角的外角等于两底角之和,是前面学习过的三角形的基本性质定理.教师适时给出引导,对此模型进行剥离:圆周角就是等腰三角形的一个底角,圆心角就是等腰三角形的外角,它们之间的数量关系刚好完全吻合.而要想出现这个定理中具备的条件,过圆周角顶点的直径很关键,是构造出模型中等腰三角形外角的点睛之笔.
3.6 模型破冰,彰显智慧
第二种位置关系,考虑转化为第一种位置关系来证明,体会数学中的转化思想.思考方向:其一要考虑第一种位置关系中的直径,其二要从圆中剥离出等腰三角形的基本模型.有了方向,学生思考起来相对容易突破.连接圆周角顶点和圆心并延长交圆周于点D,形成教材中的“折痕”,这样就把要证明的问题变成了两个“基本模型”.
已知:A,B,C是圆O上的点,∠BAC是弧BC所对的圆周角,∠BOC是弧BC所对的圆心角.
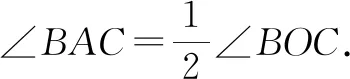
证明:连接圆周角顶点A和圆心O并延长交圆周于点D,如图4.
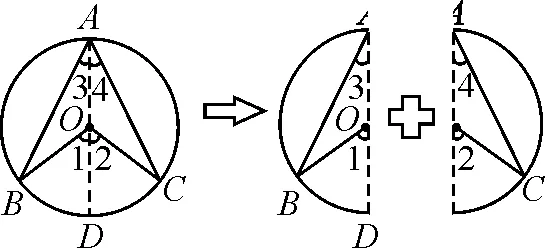
图4
∵∠3+∠4=∠BAC,∠1+∠2=∠BOC,
根据证明过程,可以形象地把第二种位置关系看成是“基本模型+基本模型”,如图4.
3.7 水到渠成,解决问题
第三种位置关系的证明难度较大,不容易观察,教师通过位置关系(2)的铺垫,去找寻基本模型.作出辅助线后,基本模型凸显,通过隐去部分线段,学生仍然能发现隐藏其中的两个基本模型,如图5.
证明:连接圆周角顶点A和圆心O并延长交圆周于点D,如图5.
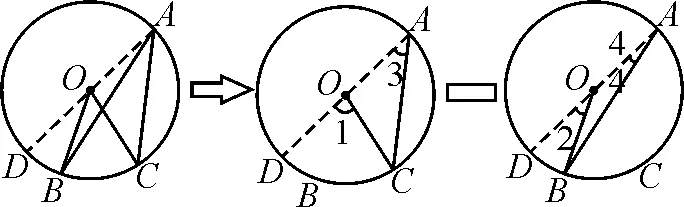
图5
∵∠3-∠4=∠BAC,∠1-∠2=∠BOC,
根据证明过程,可以形象地把第三种位置关系看成是“基本模型-基本模型”,如图5.
4 结语
至此,整节课的重点很巧妙地彰显出来,化未知为已知,将问题转化为基本数学模型[2],数学的基本思想体现无疑.在难点上也精心铺设,细化问题,通过多媒体软件的介入,连续变化达到相对严密的闭合系统,通过提炼基本模型引出辅助线、破解难点.可以说,通过这几个细节的用心处理,顺利厘清了整堂课的逻辑线,充分体现了数学学科转化思想的魅力,彰显了数学学科的育人价值.
